人脸识别和神经风格转换

人脸识别和神经风格转换

人脸识别

  1. 人脸验证(Verification)：验证输入图像是否属于某个特定身份，属于一对一问题。

    人脸识别(Recognition)：一对多问题，从大量数据中找到匹配的人脸。

    在很多人脸识别应用中，系统需要通过单一样本识别某人，而非多个样本，这就属于 One-shot Learning 问题。例如数据库中有4个员工的照片，系统需要通过一张员工的照片来判断一个人是否在数据库中。

    传统方法使用 softmax 分类器（输出5个标签），但这种方法在小规模数据集上表现不好，且随着新成员的加入，分类器需要重新训练，效率低下。

    为了有效地解决 One-shot Learning 问题，可以学习相似度函数 \(d(\text{img1}, \text{img2})\) 来计算两张图片之间的差异。如果两张图片是同一个人，输出一个很小的值，否则应该输出较大的差值。如果数据库中有新的人加入，只需将新照片添加到数据库，系统无需重新训练，可以继续通过相似度函数进行识别。与传统方法相比，这种方式具有更好的灵活性和扩展性，尤其适用于样本较少且经常有新样本加入的情况。

  2. Siamese网络是一种用于比较两张图片的网络架构。在人脸识别的背景下，它通过输入两张图片，计算它们的相似度。输入两张图片 \(x^{(1)}\) 和 \(x^{(2)}\)，输出每张图片通过网络得到的 \(128\) 维编码向量 \(f(x^{(1)})\) 和 \(f(x^{(2)})\)，分别代表两张图片的特征表示。

    然后计算两张图片编码的L2范数作为距离度量：

    \[d(x^{(1)},x^{(2)})=||f(x^{(1)})-f(x^{(2)})||_2^2 \]

    在训练时，需要满足相同人的两张图片的编码距离小，不同人的两张图片的编码距离大。

  3. 令Anchor代表基准图片，Positive代表和Anchor是同一个人，Negative代表和Anchor不是同一个人。Siamese网络采用三元组损失函数(Triplet Loss)，目标是让A与P之间的特征距离尽可能小，而A与N之间的特征距离尽可能大。损失函数为：

    \[L(A,P,N)=max(||f(A)-f(P)||^2+||f(A)-f(N)||^2+\alpha, 0) \]

    这里的 \(\alpha\) 是间隔(Margin)超参数，衡量了 \(||f(A)-f(P)||^2 < ||f(A) - f(N)||^2\) 的程度。

    为了有效地训练网络，训练数据集需要包含成对的Anchor和Positive图片。一般来说，数据集中的每个人会有多个不同角度或条件下的照片，这样就可以构造有效的三元组 \((A,P,N)\)。如果数据集中每个人只有一张照片，就无法构造出有效的三元组，影响训练效果。

  4. 也可以将人脸验证问题视作二分类问题，通过Siamese网络架构生成图片的特征编码，并利用逻辑回归或其他分类器判断两张图片是否属于同一个人。

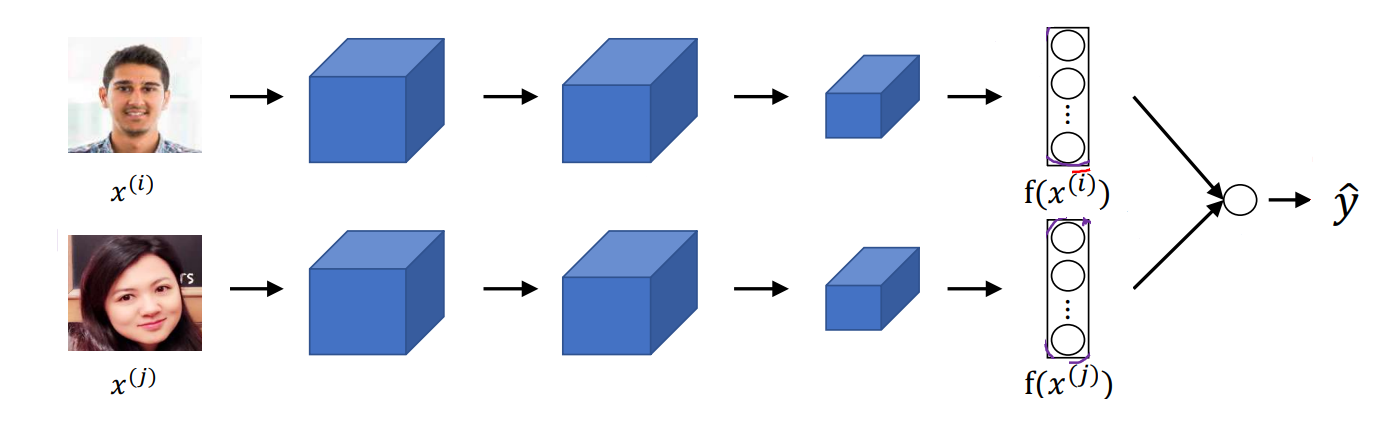
    https://cdn.acwing.com/media/article/image/2025/01/25/181746_681f9ed6da-bc.png

    首先对两张图片进行特征提取，提取出128维嵌入向量 \(f(x^{(i)})\) 和 \(f(x^{(j)})\)。然后利用 \(\chi^2\) 公式计算特征编码之间的差异。

    \[\frac{(f(x^{(i)})_k - f(x^{(j)})_k)^2}{f(x^{(i)})_k + f(x^{(j)})_k} \]

    最后将特征差异输入到逻辑回归中，计算分类概率：

    \[\hat{y}=\text{Sigmoid}(\sum_{k=1}^{128}\omega_k|f(x^{(i)})_k-f(x^{(j)})_k|+b) \]

    在训练过程中，需要对两个分支共享参数，逻辑回归权重进行学习。

    在实际应用中，通常对数据库中的图片，提前通过网络计算并存储其特征编码。新图片只需通过网络生成编码并与数据库中的编码比较，避免重复计算，大幅提升效率。

    二分类方法仅需要成对的图片进行训练，模型直接输出是否为同一人，更简单直接。但是对于大规模数据集，可能不如 Triplet Loss 的特征分布效果好。

神经风格迁移

  1. 神经风格迁移是一种基于卷积神经网络的图像生成技术，将一张图片的内容(Content)和另一张图片的风格(Style)融合，生成一张新的图片Generation，它同时保留内容图片的结构和风格图片的艺术风格。

    https://cdn.acwing.com/media/article/image/2025/01/25/181746_1e340660db-styletrans.png

  2. CNN 的不同层次学习到的特征从浅层到深层逐步复杂化。

    可以对隐藏单元进行可视化，通过找到训练集中最大化激活某隐藏单元的图片块，观察这些图片块的共性，理解隐藏单元对哪些特征敏感。

    https://cdn.acwing.com/media/article/image/2025/01/26/181746_ce7e0148db-visual.png

    浅层学习简单的特征，如边缘、线条、颜色阴影等。

    中层学习更加复杂的局部模式，如图案、纹理、几何形状。

    深层学习语义级别的特征，如物体的具体部件或完整物体（如人、车、动物等）。

    浅层隐藏单元接受域小，仅关注局部区域（如图片的一小块）。随着层次加深，接受域逐渐增大，隐藏单元能感知图片的更大区域，甚至可以捕获整张图片的全局信息。

  3. 需要定义一个代价函数 \(J(G)\) 来衡量生成图片的好坏，通过最小化 \(J(G)\) 生成最终图像。

    代价函数 \(J(G)\) 由两部分组成：

    • 内容代价函数 \(J_{\text{content}}(C, G)\)：衡量生成图片 \(G\) 和内容图片 \(C\) 在内容上的相似性。
    • 风格代价函数 \(J_{\text{style}}(S, G)\)：衡量生成图片 \(G\) 和风格图片 \(S\) 在风格上的相似性。

    因此，完整的代价函数为：

    \[J(G)=\alpha J_{\text{content}}(C, G)+\beta J_{\text{style}}(S, G) \]

    \(\alpha\) 和 \(\beta\) 是超参数，用于控制内容和风格在最终图像中的相对重要性。

    在神经风格迁移中，算法流程如下：

    • 随机初始化生成图片 \(G\)：通常用随机噪声图像初始化 \(G\)，大小可以是任意尺寸，如 \(100 \times 100 \times 3\) 或 \(500 \times 500 \times 3\)。

    • 计算代价函数 \(J(G)\)：使用前面定义的代价函数评估生成图片 \(G\) 的好坏。

    • 梯度下降优化 \(G\)：不断更新生成图片 \(G\) 的像素值，使代价函数 \(J(G)\) 最小化：

      \[G:=G-\frac{\partial J(G)}{\partial G} \]

      在优化过程中，生成图片逐渐从随机噪声演变为同时具有内容图片结构和风格图片艺术风格的图像。

      https://cdn.acwing.com/media/article/image/2025/01/26/181746_4c833becdb-gen.png

  4. 内容代价函数 \(J_{\text{content}}(C, G)\) 用于衡量生成图片 \(G\) 和内容图片 \(C\) 在内容上的相似度。通过最小化内容代价函数，生成图片 \(G\) 可以保留内容图片 \(C\) 的主要结构和布局。

    内容代价是通过选定某一层的激活值计算的：

    • 如果选择浅层（如第一层），生成图片 \(G\) 将在像素级别接近内容图片 \(C\)。
    • 如果选择深层，生成图片 \(G\) 会更关注高层次语义（如图像中的具体物体）。
    • 通常选择网络的中间层，如 VGG 网络中的中间卷积层，可以兼顾像素级别和语义级别的特征。

    对于内容图片 \(C\) 和生成图片 \(G\)，在选定层 \(l\) 的激活值分别记为 \(a^{[l][C]}\) 和 \(a^{[l][G]}\)。内容代价函数定义为：

    \[J_{\text{content}}(C, G) = \frac{1}{2}||a^{[l][C]}-a^{[l][G]}||^2 \]

  5. 如果描述一幅画的内容，可能会提到画中有什么（如一座桥、几个人、一条河），它们的布局是什么（桥在中央，河流穿过画面）。

    而风格是描述这幅画的“艺术手法”，它关注的不是“画了什么”，而是“怎么画的”，包括线条和笔触是流畅的还是粗犷的，画面中是否有重复的几何图案或纹理，整体是暖色调还是冷色调，颜色是均匀的还是对比强烈，某些特定纹理（如波浪线）是否总出现在特定的颜色区域中。

    例如梵高的《星空》或莫奈的印象派画作，风格包括流动的线条和强烈的笔触，颜色是明亮且对比强烈的（如蓝色和黄色的旋涡），纹理有涡旋状的重复模式。

    在神经网络中，“风格”的具体含义可以从特征图的相关性角度理解。特征图的每个通道提取了图像中的某种特征，例如垂直纹理、颜色变化、局部形状等，可以通过风格矩阵（Gram矩阵）来描述各通道之间的相关性。

    具体来说，如果“蓝色区域”与“垂直线条”经常同时出现在图像中，则它们具有较高的相关性。如果“圆形纹理”与“黄色区域”几乎没有共同出现，则相关性较低。

    通过比较风格图片和生成图片的风格矩阵，神经风格迁移算法可以调整生成图片的纹理和颜色分布，使其更接近目标风格图片。

    风格矩阵：

    \[G_{kk'}^{[l]} = \sum_{i=1}^{n_H^{[l]}} \sum_{j=1}^{n_W^{[l]}} a_{i,j,k}^{[l]} a_{i,j,k'}^{[l]} \]

    其中，\(a_{i,j,k}^{[l]}\) 表示风格图片 \(S\) 在第 \(l\) 层 \((i,j,k)\) 位置的激活值，\(n_H^{[l]}\), \(n_W^{[l]}\), \(n_C^{[l]}\) 表示第 \(l\) 层的高度、宽度和通道数，\(k, k'\) 表示通道索引。

    \(G_{kk'}\) 衡量通道 \(k\) 和通道 \(k'\) 特征在整个图像中的共同出现强度。如果 \(G_{kk'}\) 值大，表示这两个特征经常一起出现在图像中，如果 \(G_{kk'}\) 值小，表示这两个特征的出现没有明显关联。

    那么风格代价函数定义为：

    \[J_{\text{style}}^{[l]}(S, G) =\frac{1}{4 n_C^{[l]} n_W^{[l]} n_H^{[l]}} \|G^{l} - G^{l}\|_F^2= \frac{1}{4 n_C^{[l]} n_W^{[l]} n_H^{[l]}} \sum_{k=1}^{n_C^{[l]}} \sum_{k'=1}^{n_C^{[l]}} \left(G_{kk'}^{l} - G_{kk'}^{l}\right)^2 \]

    为了更全面地捕捉风格，可以结合多个层的风格信息，综合风格代价函数如下：

    \[J_{\text{style}}(S, G) = \sum_l \lambda^{[l]} J_{\text{style}}^{[l]}(S, G) \]

    其中，\(\lambda^{[l]}\) 是每层风格代价的权重，用于平衡不同层的贡献。

  6. 卷积神经网络不仅适用于2D图像数据，还可以扩展到1D和3D数据。

    1D卷积网络，输入序列数据，滑动窗口沿轴滑动，生成特征图，如处理心电图、语音信号等。

    3D卷积网络，输入 \(n_H \times n_W \times n_D \times n_C\) 尺度的高维数据，卷积核沿着高、宽、深三个维度滑动，生成三维特征图，如处理视频数据、CT扫描等。

    一维卷积可以提取局部时间序列特征，但缺乏长期依赖建模能力，而 RNN 更擅长捕捉长时间序列中的依赖关系。

    二维卷积适合处理静态图像，三维卷积适合处理空间-时间或体积数据，虽然计算复杂度更高，但能够捕捉更丰富的空间-时间特征。

posted @ 2025-01-26 11:33  钰见梵星  阅读(33)  评论(0)    收藏  举报