【机器学习】线性回归

本博客只记录基本知识，不涉及模型的推导。详细过程请参考文末 Reference

回归模型的数学定义

假设模型的输入数据为 \(d\) 维向量 \(\vec{x}\)，输出 \(y\) 为连续型。回归模型等价于寻找一个函数\(f\)，建立\(\vec{x}\)到\(y\)的映射关系\(y=f(x)\)

1 线性回归

1.1 线性回归的基本假设

1. 输入特征是非随机的且互不相关
2. 随机误差具有零均值、同方差的特点，且彼此不相关
3. 输入特征与随机误差不相关
4. 随机误差项服从正态分布 \(N(0,\sigma^2)\)

1.2 一元线性回归

模型：\(y=w_1x+w_0\)，使用最小化残差平方和 \(\min RSS(w_1,w_0)\) 求解(OLS)，最优解为

\[\hat{w}_1=\frac{\sum\limits_{i=1}^nx_i^2-n\bar{x}\bar{y}} {\sum\limits_{i=1}^nx_i^2-n(\bar{x})^2},\quad \hat{w_0}=\bar{y}-\hat{w}_1\bar{x} \]

1.3 多元线性回归

模型：\(y=\boldsymbol{w}^T\boldsymbol{x}\)，输出\(\hat{\boldsymbol{y}}=\boldsymbol{X}\boldsymbol{w}\)，残差平方和\(RSS(\boldsymbol{w})=||\boldsymbol{y}-\boldsymbol{X}\boldsymbol{w}||_2^2\)，最优解\(\hat{\boldsymbol{w}}=(\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{y}\)

1.4 回归结果诊断的重要性：安斯库姆四重奏（Anscombe's quartet）

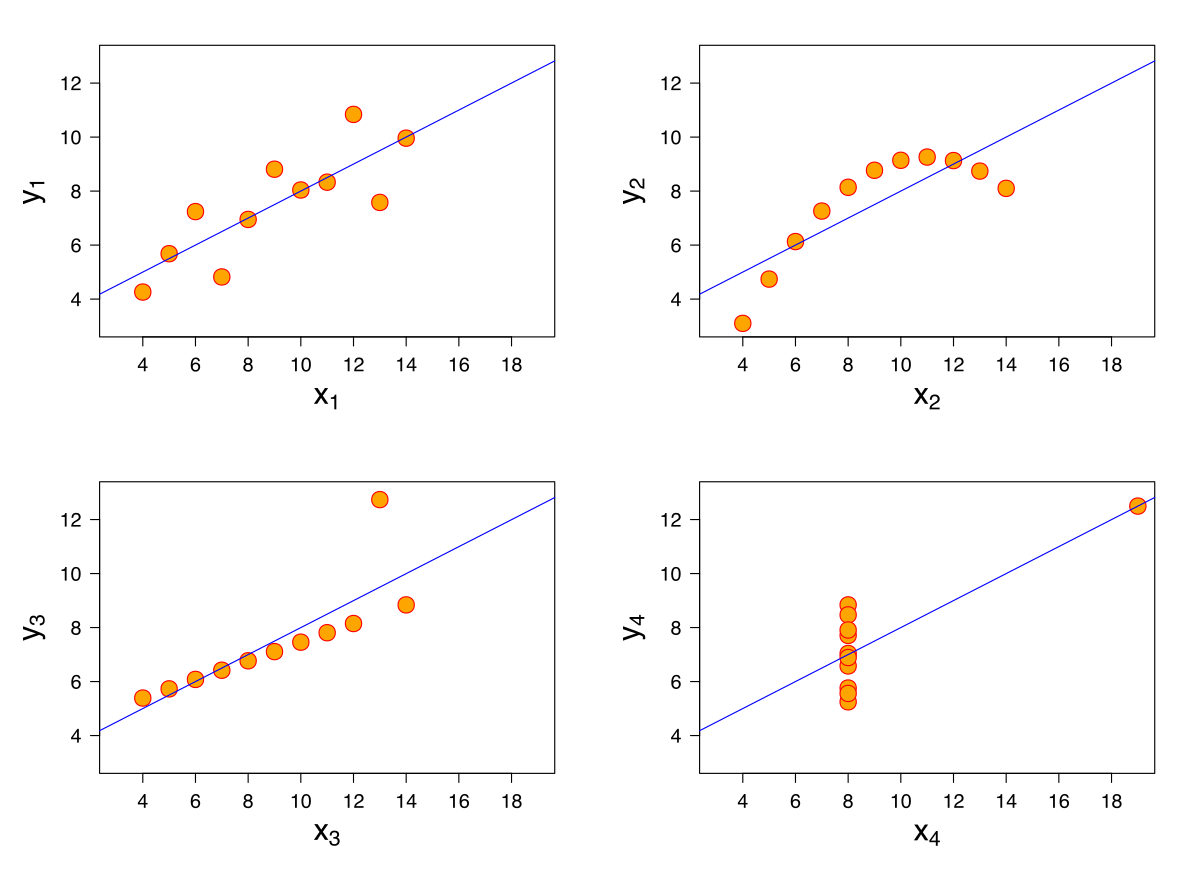
1.5 衡量指标：决定系数\(R^2\)，均方根误差\(RMSE\)

2 线性回归正则化

2.1 岭回归和 LASSO

本质就是 L2 正则和 L1 正则。

• 岭回归：\(l_2\)正则化，\(\min\limits_{\boldsymbol{w}}||\boldsymbol{y}-\boldsymbol{X}\boldsymbol{w}||_2^2,\ s.t.\ ||\boldsymbol{w}||_2\le C \Leftrightarrow \min\limits_{\boldsymbol{w}}||\boldsymbol{y}-\boldsymbol{X}\boldsymbol{w}||_2^2+\lambda||\boldsymbol{w}||_2^2,\ \lambda>0\)
• LASSO：\(l_1\)正则化，\(\min\limits_{\boldsymbol{w}}||\boldsymbol{y}-\boldsymbol{X}\boldsymbol{w}||_2^2,\ s.t.\ ||\boldsymbol{w}||_1\le C\Leftrightarrow \min\limits_{\boldsymbol{w}}||\boldsymbol{y}-\boldsymbol{X}\boldsymbol{w}||_2^2+\lambda||\boldsymbol{w}||_1^2,\ \lambda>0\)

利用拉格朗日乘子法，约束优化问题等价于无约束惩罚函数优化问题。正则化的本质是偏差（bias）和方差（variance）的平衡。

• 岭回归有解析表达式\(\boldsymbol{w}^{ridge}=\arg\min\limits_{\boldsymbol{w}}(||\boldsymbol{y}-\boldsymbol{X}\boldsymbol{w}||_2^2+\lambda||\boldsymbol{w}||_2^2)=(\boldsymbol{X}^T\boldsymbol{X}+\lambda\boldsymbol{I})^{-1}\boldsymbol{X}^T\boldsymbol{y}\)，正则项\(\lambda\boldsymbol{I}\)使得多重共线性时，\(\boldsymbol{X}^T\boldsymbol{X}\)接近奇异，岭回归还是能得到稳定结果。
• LASSO 没有解析解，但\(\boldsymbol{w}^{LASSO}\)是稀疏的，很多分量接近 0，有助于选择。

1. LASSO 求解方法

坐标下降法（coordinate descent），LARS 算法，基于近似的梯度方法（proximal gradient）的 ISTA（Iterative Shrinkage-Thresholding Algorithm）和 FISTA。ISTA 算法如下：

最小化一个光滑函数\(f(\boldsymbol{w})\)，梯度下降法基于当前变量值\(\boldsymbol{w}^{(t)}\)迭代：\(\boldsymbol{w}^{(t+1)}=\boldsymbol{w}^{(t)}-\eta\nabla f(\boldsymbol{w}^{(t)})\)，\(\eta\)是学习率

梯度下降的近似形式：\(\boldsymbol{w}^{(t+1)}=\arg\min\limits_\boldsymbol{w} f(\boldsymbol{w}^{(t)})+\nabla f(\boldsymbol{w}^{(t)})^T(\boldsymbol{w}-\boldsymbol{w}^{(t)})+\frac1{2\eta}||\boldsymbol{w}-\boldsymbol{w}^{(t)}||_2^2\)

如果最小化\(f+g\)，则

\[\begin{aligned} \boldsymbol{w}^{(t+1)}=&\arg\min\limits_\boldsymbol{w} f(\boldsymbol{w}^{(t)})+\nabla f(\boldsymbol{w}^{(t)})^T(\boldsymbol{w}-\boldsymbol{w}^{(t)})+\frac1{2\eta}||\boldsymbol{w}-\boldsymbol{w}^{(t)}||_2^2+g(\boldsymbol{w})\\ =&\arg\min\limits_{\boldsymbol{w}}g(\boldsymbol{w})+\frac1{2\eta}||\boldsymbol{w}-(\boldsymbol{w}^{(t)}-\eta\nabla f(\boldsymbol{w}^{(t)}))||_2^2 \end{aligned} \]

LASSO 的目标函数\(f(\boldsymbol{w})=\frac12||\boldsymbol{y}-\boldsymbol{X}\boldsymbol{w}||_2^2\)，\(g(\boldsymbol{w})=\lambda||\boldsymbol{w}||_1\)，\(f\)的梯度\(\nabla f(\boldsymbol{w})=\boldsymbol{X}^T(\boldsymbol{X}\boldsymbol{w}-\boldsymbol{y})\)故迭代公式为

\[\boldsymbol{w}^{(t+1)}=\arg\min\limits_\boldsymbol{w}\lambda||\boldsymbol{w}||_1+\frac1{2\eta}||\boldsymbol{w}-(\boldsymbol{w}^{(t)}-\eta\nabla f(\boldsymbol{w}^{(t)}))||_2^2\\ \boldsymbol{w}^{(t+1)}=S_{\eta\lambda}(\boldsymbol{w}^{(t)}-\eta\nabla f(\boldsymbol{w}^{(t)}))\\ \]

其中\(S_{\eta\lambda}(\boldsymbol{v})\)代表软阈值操作（soft thresholding operator），

\[(S_a(\boldsymbol{v}))_i=\left\lbrace \begin{aligned} &v_i-a, && if\quad v_i>a&\\ &0, && if\quad |v_i|\le a&\\ &v_i+a, && if\quad v_i<-a&\\ \end{aligned} \right. \]

2. 为社么 LASSO 可以产生稀疏解

从优化理论可知，最优解发生在目标函数的等高线和可行区域的交集处。角比边更容易和等高线相交，在高维情况下尤其明显，因为高维的角更加凸出。而\(l_2\)球可能相交于任意点，所以不容易产生稀疏解。

3. 正则化路径分析

正则化路径是指回归系数的估计值\(\hat{\boldsymbol{w}}\)随着正则化系数增大而变化的曲线，可以分析特征之间相关性和进行特征选择。

岭回归的正则化路径被称为岭迹。岭迹波动很大说明该特征与其他特征有相关性。标准化的特征可以直接比较回归系数的大小，回归系数比较稳定且绝对值很小的特征可以去除。回归系数不稳定且震动趋于零的特征也可以去除。

LASSO 回归当\(\lambda\)很大时所有特征的系数都被压缩到 0，但系数减小是逐个进行的，可以通过控制\(\lambda\)选择特征个数。

2.2 其他正则化的线性回归模型

问题：LASSO 特征只会选择高度相关特征中的一个，实际中有时需要全部选择。

弹性网络（elastic net）正则化：\(J(\boldsymbol{w})=||\boldsymbol{y}-\boldsymbol{X}\boldsymbol{w}||_2^2+\lambda_1||\boldsymbol{w}||_1+\lambda_2||\boldsymbol{w}||_2^2\)，具有特征分组的效果：高度相关的特征系数趋于相等（负相关的特征有符号）

Group LASSO：事先确定\(G\)组\(\boldsymbol{w}=(\boldsymbol{w}_1,\boldsymbol{w}_2,\cdots,\boldsymbol{w}_G)\)，目标函数\(J)\boldsymbol{w})=||\boldsymbol{y}-\boldsymbol{X}\boldsymbol{w}||_2^2+\sum\limits_{g=1}^{G}\lambda_g||\boldsymbol{w}_g||_2^2\)

Reference

1. 《数据科学导引》，欧高炎、朱占星、董彬、鄂维南，高等教育出版社

2. 《机器学习》，周志华，清华大学出版社

3. Machine Learning. Andrew Ng. Coursera