堆
1. 树的基本概念
树与链表,栈和队列不同, 是一种非线性的数据结构, 它由n (n>=0) 个有限结点组成一个具有层次关系的集合
把它叫做树,是因为存储在内存中的数据, 在逻辑上呈现一种树的形态, 只是根在上,叶在下

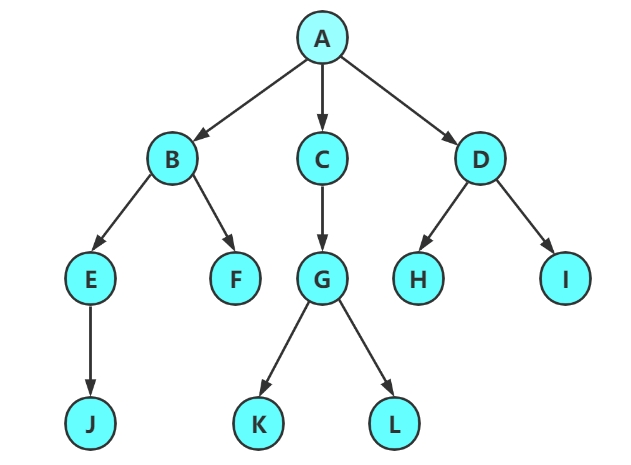
其次, 每一棵树都可以分为根(根结点)和子树(子节点), 子树又可以分为根和子树
树的结点关系由人类亲缘关系来解释
- 节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
- 叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I…等节点为叶节点。
- 非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G…等节点为分支节点。
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点。
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点。
- 兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点。
- 树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度:树中节点的最大层次; 如上图:树的高度为4。
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点。
- 节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先。
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙。
- 森林:由m(m>0)棵互不相交的树的集合称为森林
其中, 粗字体表示需要重点理解, 剩下的作为了解
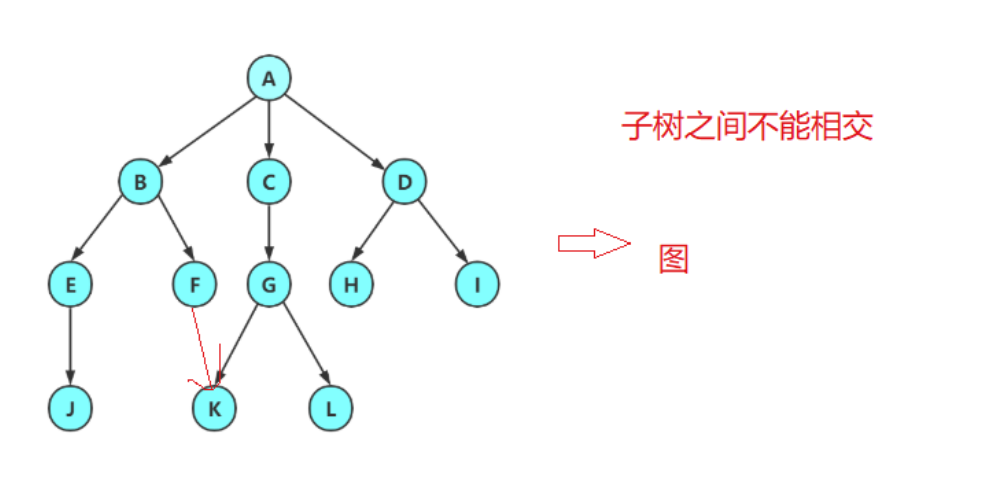
最后, 子树之间不能有交集,否则就是图
2. 二叉树
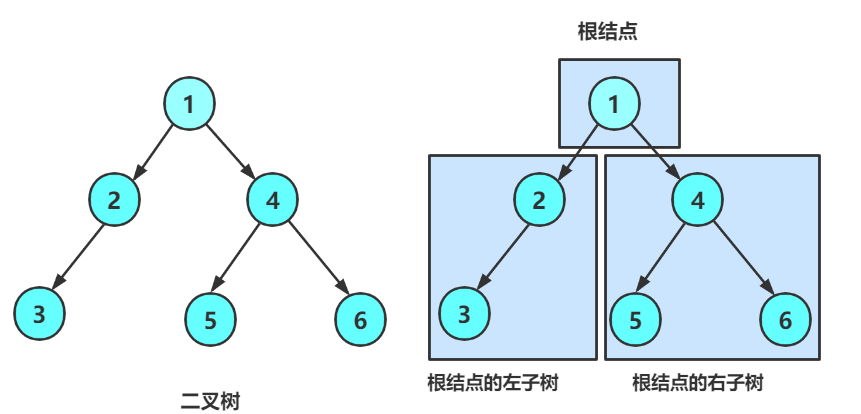
二叉树的概念
二叉树是一组结点的集合, 每一个结点的度可以是1,2, 但是绝对不能大于2, 否则就不是一颗二叉树
什么是满二叉树/完全二叉树
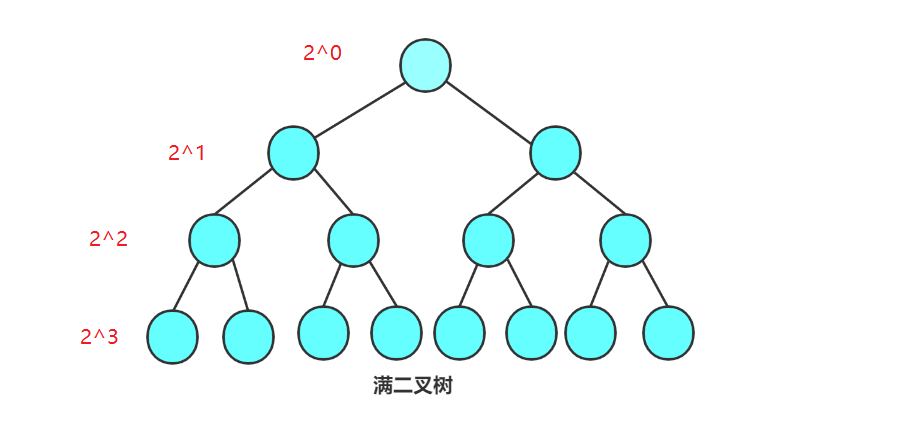
满二叉树, 就是每一层的结点数量都达到最大值, 如上图
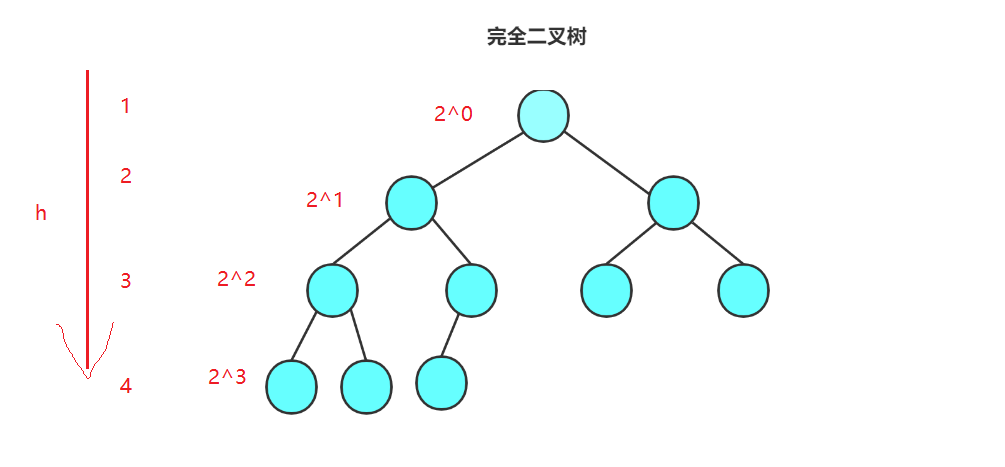
完全二叉树, 前h-1层是满的, 最后一层从左往右必须是连续的
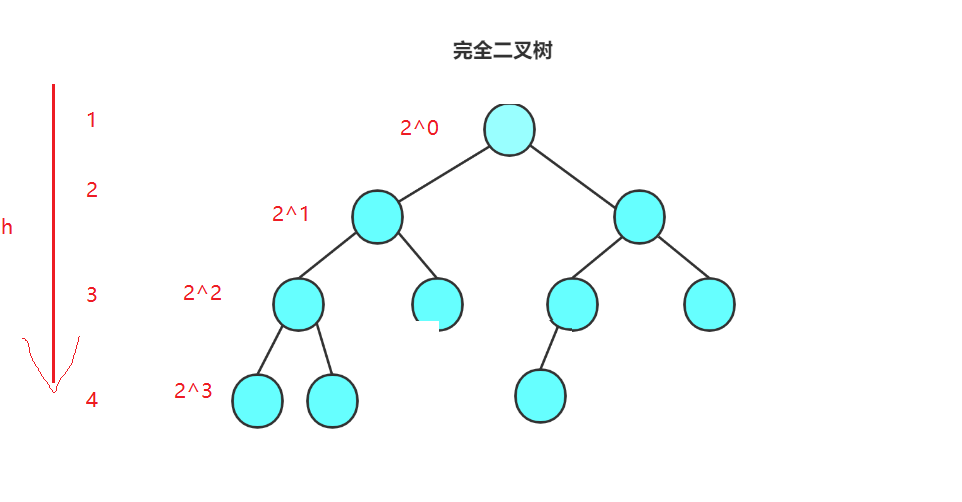
如图, 如果是这样,就不是一颗完全二叉树
满二叉树结点个数和完全二叉树结点范围
因为满二叉树的每一层都是满的, 所以结点的数量是固定的
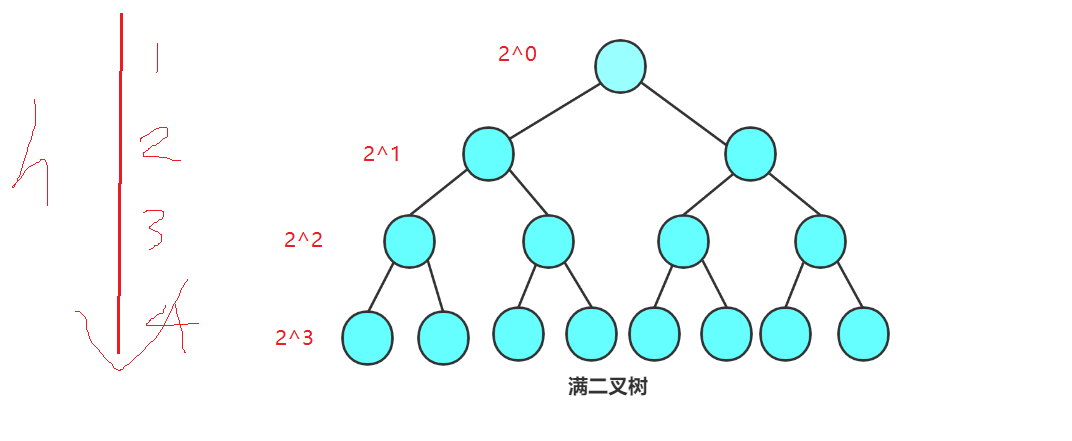
假设满二叉树的高度为h, 推导公式:
F(h) = 2^0 + 2^1 + 2^2 ... 2^(h-2) + 2^(h-1)
用错位相减法解:
2*F(h) = 2^1 + 2^2 + 2^3 + ............. + 2^(h-1) + 2^(h)
-
F(h) = 2^0 + 2^1 + 2^2 + ..... + 2^(h-2) + 2^(h-1)
F(h) = 2^h - 1
高度为h的满二叉树, 有 2^h-1个结点

完全二叉树最多结点数量: 等于满二叉树结点数量, 2^h-1
完全二叉树最少结点数量: 最后一层最少一个结点, 前h-1层是满的
推导公式:
F(h) = 2^0 + 2^1 + ... + 2^h-2 + 1
还是用错位相减法先求出前h-1层的结点数量:
2 * F(h) = 2^1 + 2^2 + ... + 2^h-1
-
F(h) = 2^0 + 2^1 + ... + 2^h-2
= -1 + 2^h-1
然后+1, 因为最后一层最少一个结点, 完全二叉树最少结点数量: 2^(h-1)
完全二叉树结点范围: [ 2^(h-1), 2^h - 1]
3. 堆的概念
堆的基本概念
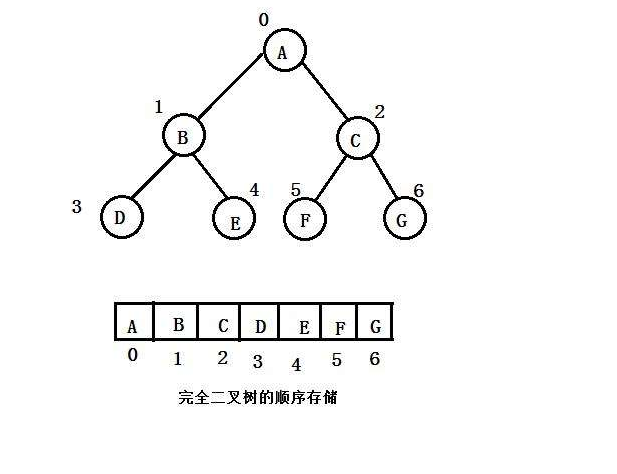
通过观察完全二叉树, 可以发现完全二叉树非常适合用数组进行存储
更为重要的是, 通过数组的下标关系可以用孩子找到父亲,父亲也可以找到孩子
比如图中:
D(孩子)的下标(3)-1除2, 可以得到B(父亲)的下标
父亲(B) * 2 + 1, 得到D(孩子)下标
父亲(B) * 2 + 2, 得到E(孩子)下标
所以可以得出结论:
leftchild = parent*2+1
rightchild = parent*2+2
parent = (child-1) / 2
什么是堆
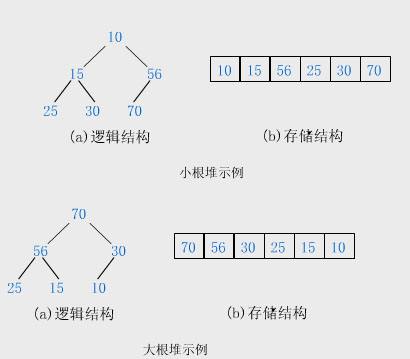
从本质上(物理结构)来看, 堆是一个数组, 但是从逻辑结构来看, 堆是一棵完全二叉树
数组都可以看作是一颗完全二叉树, 但是不能看作是堆
判断数组是否是一个堆, 必须满足一个条件: 所有父亲大于或者等于孩子 --- 大根堆 / 满足所有父亲小于或者等于孩子 --- 小根堆
4. 堆的实现
heap.h
#include <stdio.h>
#include <assert.h>
#include <stdbool.h>
#include <stdlib.h>
typedef int HPDataType;
typedef struct heap
{
HPDataType* dys;
int capcacity;
int size;
}HP;
// 初始化与销毁
void HeapInit(HP* php);
void HeapDestroy(HP* php);
// 向上调整算法
void AdjustUp(HPDataType* dys, int child);
// 向下调整算法
void AdjustDown(HPDataType* dys, int parent, int sz);
void HeapPush(HP* php, HPDataType data);
void HeapPop(HP* php);
HPDataType HeapTop(HP* php);
bool isEmpty(HP* php);heap.c
#include "heap.h"
// 初始化与销毁
void HeapInit(HP* php)
{
assert(php);
HPDataType* tmp = (HPDataType*)malloc(sizeof(HPDataType) * 4);
if (NULL == tmp)
{
perror("HeapInit::malloc fail");
return;
}
php->dys = tmp;
php->size = 0;
php->capcacity = 4;
}
void HeapDestroy(HP* php)
{
assert(php);
free(php->dys);
php->dys = NULL;
php->capcacity = 0;
php->size = 0;
}
void Swap(HPDataType* buf1, HPDataType* buf2)
{
int tmp = *buf1;
*buf1 = *buf2;
*buf2 = tmp;
}
// 向上调整算法
void AdjustUp(HPDataType* dys, int child)
{
assert(dys);
int parent = (child - 1) / 2;
while (child > 0)
{
if (dys[child] > dys[parent])
{
Swap(&dys[child], &dys[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
// 向下调整算法
void AdjustDown(HPDataType* dys, int parent, int sz)
{
assert(dys);
int child = parent * 2 + 1;
while (child < sz)
{
// 假设左孩子大于右孩子
if (child+1 < sz && dys[child + 1] > dys[child])
{
child++;
}
if (dys[child] > dys[parent])
{
Swap(&dys[child], &dys[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
// 进堆
void HeapPush(HP* php, HPDataType data)
{
assert(php);
if (php->size == php->capcacity)
{
HPDataType* tmp = (HPDataType*)realloc(php->dys, php->capcacity * sizeof(HPDataType) * 2);
if (NULL == tmp)
{
perror("HeapPush::realloc fail");
return;
}
php->dys = tmp;
php->capcacity *= 2;
}
php->dys[php->size] = data;
php->size++;
AdjustUp(php->dys, php->size - 1);
}
// 删除堆顶数据
void HeapPop(HP* php)
{
assert(php);
assert(!isEmpty(php));
Swap(&php->dys[0], &php->dys[php->size - 1]);
php->size--;
AdjustDown(php->dys, 0, php->size);
}
bool isEmpty(HP* php)
{
assert(php);
return php->size == 0;
}
HPDataType HeapTop(HP* php)
{
assert(php);
assert(!isEmpty(php));
return php->dys[0];
}
int HPSize(HP* php)
{
assert(php);
return php->size;
}test.c
#include "heap.h"
int main()
{
HP heap;
HeapInit(&heap);
HeapPush(&heap, 1);
HeapPush(&heap, 2);
HeapPush(&heap, 3);
HeapPush(&heap, 5);
HeapPush(&heap, 6);
while (!isEmpty(&heap))
{
printf("%d ", HeapTop(&heap));
HeapPop(&heap);
}
}5. 堆的实际应用1 - 堆排序
通过数据结构堆进行排序
将数组元素依次插入到堆中, 模拟建队的过程
然后分别取出堆顶数据放回到数组中, 模拟排序
#include "heap.h"
void heapsort(int* array, int sz)
{
HP heap;
HeapInit(&heap);
// 将数组元素依次入堆
for (int i = 0; i < sz; i++)
{
HeapPush(&heap, array[i]);
}
// 分别取出堆顶数据, 然后入数组
int i = 0;
while (!isEmpty(&heap))
{
array[i++] = HeapTop(&heap);
HeapPop(&heap);
}
HeapDestroy(&heap);
}
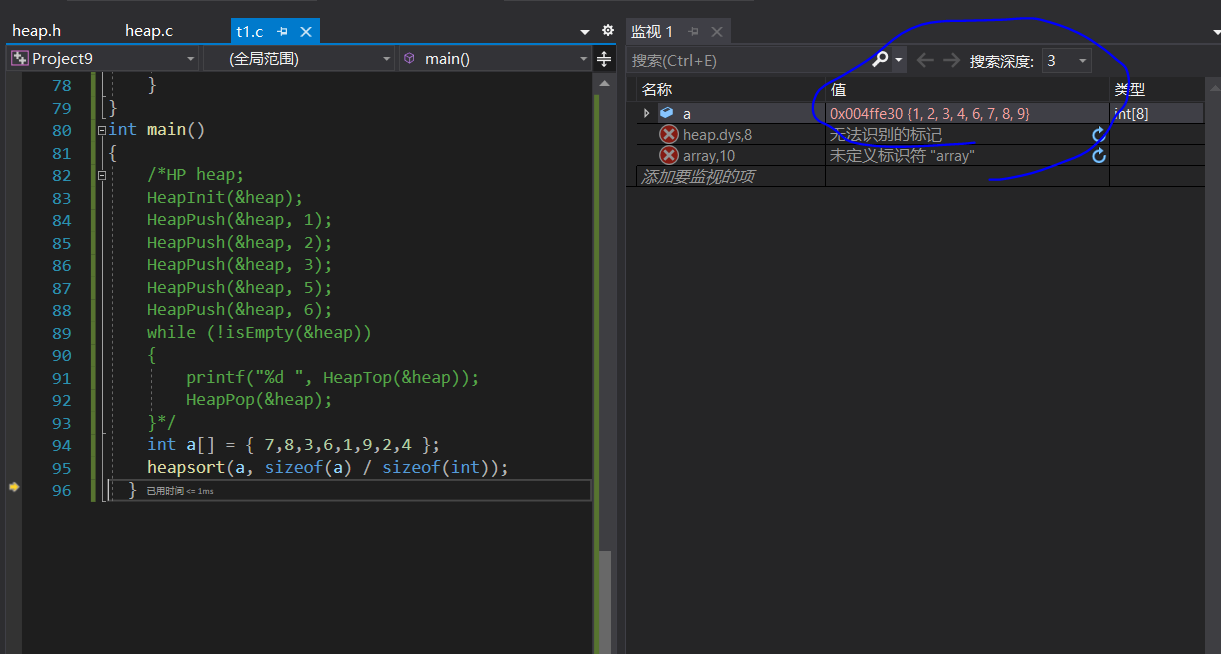
int main()
{
int a[] = { 7,8,3,6,1,9,2,4 };
heapsort(a, sizeof(a) / sizeof(int));
} 
如图, 通过堆进行了排序
但是这种方法并不好, 因为建堆开辟空间, 空间复杂度为O(N), 其次每次排序都需要一个数据结构堆, 很麻烦
下面来看一种最优的方法
向上/下调整建堆排序
#include "heap.h"
void heapsort(int* array, int n)
{
// 向上调整建堆
for (int i = 1; i < n; i++)
{
AdjustUp(array, i);
}
// 向下调整建堆
/*for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(array, i, n);
}*/
int end = n - 1;
while (end > 0)
{
Swap(&array[0], &array[end]);
AdjustDown(array, 0, end);
end--;
}
}
int main()
{
int a[] = { 7,8,3,6,1,9,2,4 };
heapsort(a, sizeof(a) / sizeof(int));
}向上调整建堆, 将数组从第2个元素(下标为1)开始依次向上调整,将数组建成一个堆
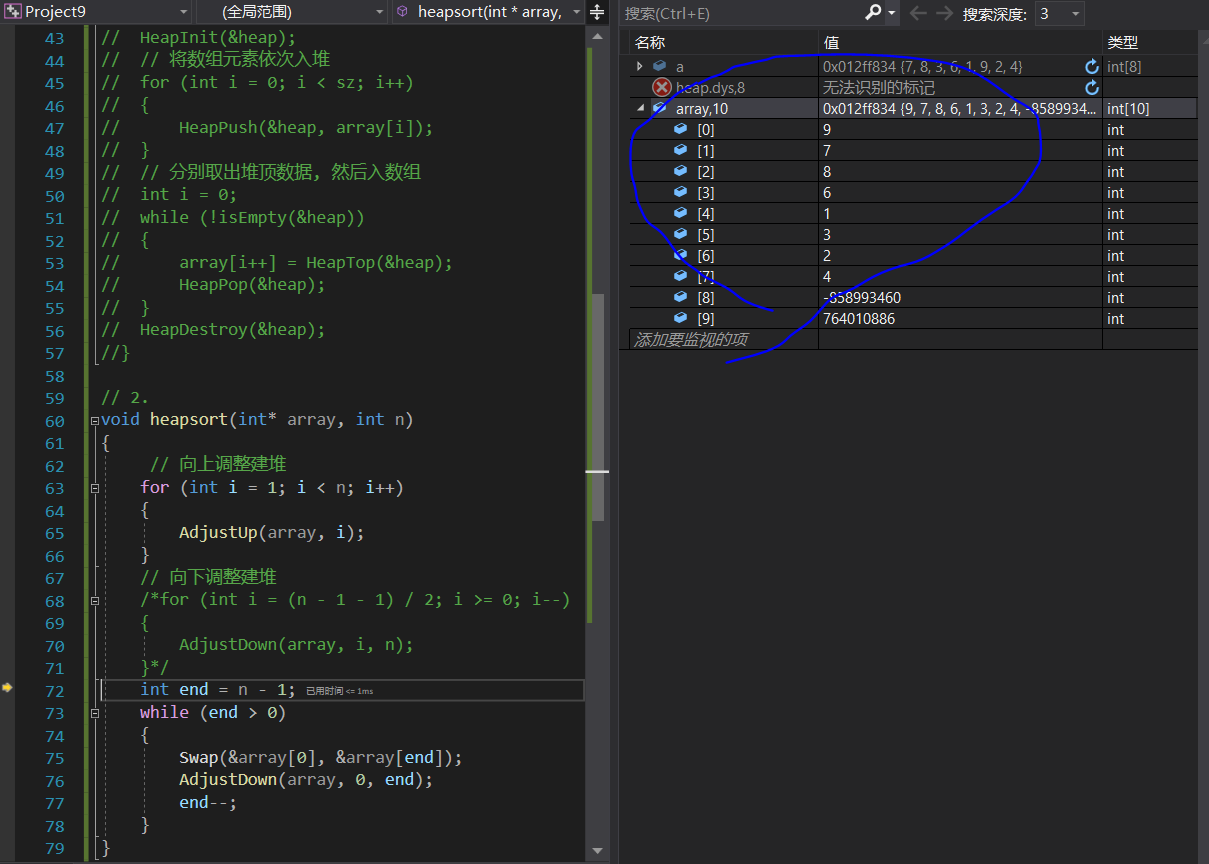
然后通过一个非常巧妙的方法, 模拟排序
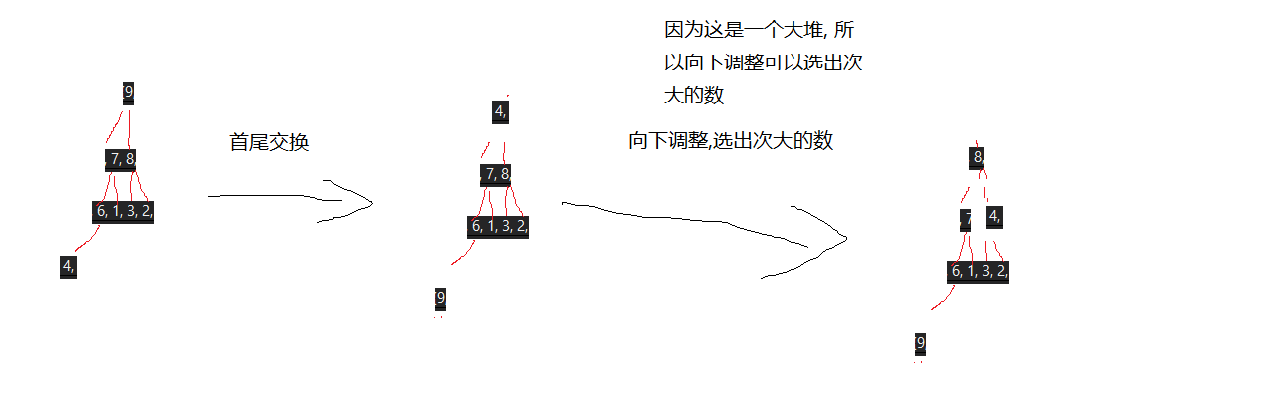
按照这个原理, 最终数组会从小到大进行排序
最后根据这个例子可以得出一个结论:
排升序, 建大堆
排降序, 建小堆
下面再来看一下, 向下调整建堆
void heapsort(int* array, int n)
{
// 向上调整建堆
/*for (int i = 1; i < n; i++)
{
AdjustUp(array, i);
}*/
// 向下调整建堆
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(array, i, n);
}
int end = n - 1;
while (end > 0)
{
Swap(&array[0], &array[end]);
AdjustDown(array, 0, end);
end--;
}
}
int main()
{
int a[] = { 7,8,3,6,1,9,2,4 };
heapsort(a, sizeof(a) / sizeof(int));
}向下调整建堆, 首先需要找到第一个结点的父亲, 然后依次递减向下调整建堆, 如下图
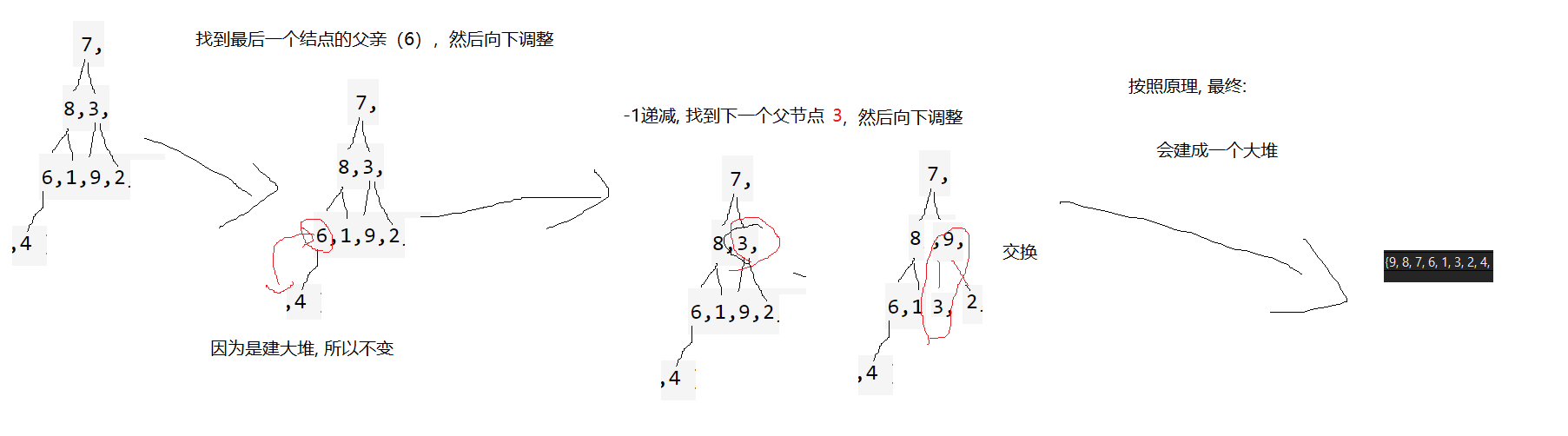
现在知道向上/向下调整如何建堆, 建堆后如何排序, 然后排升序, 建大堆, 排降序, 建小堆
那么, 向上调整和向下调整在效率上有什么区别吗?
结论是, 向下调整在效率上更优, 下面进行证明
向上/向下调整建堆复杂度证明
首先, 计算向下调整建堆复杂度
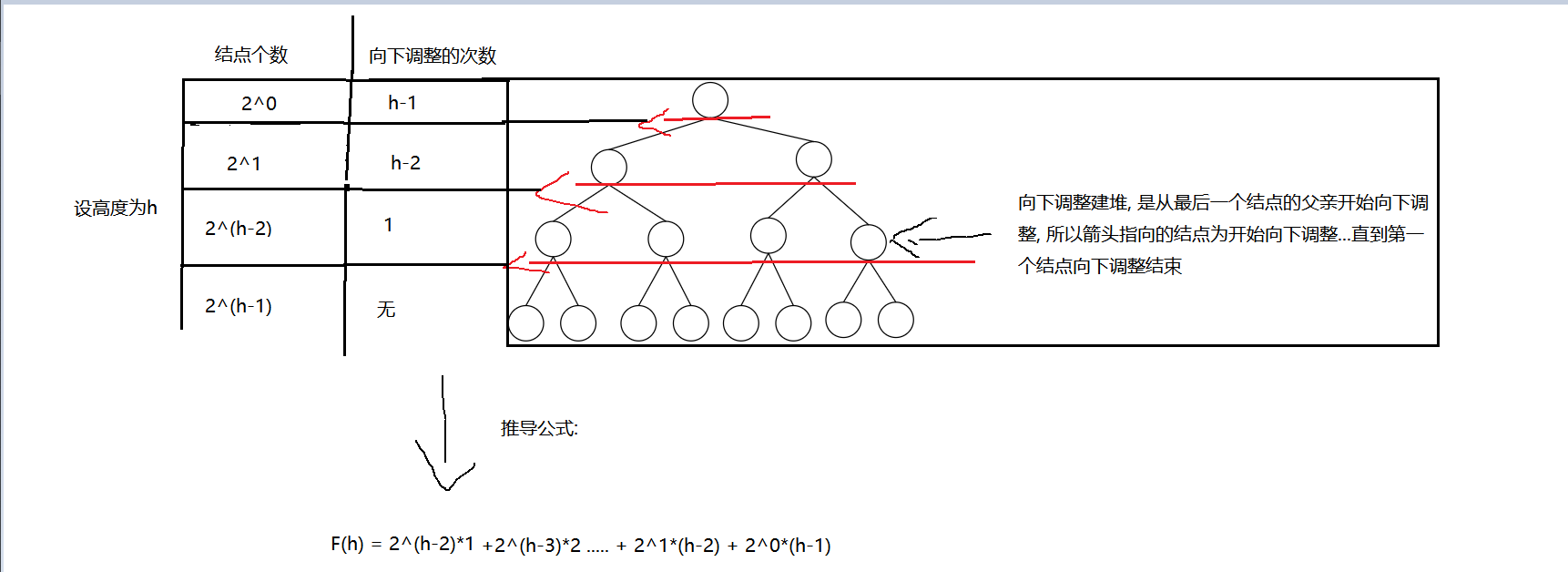
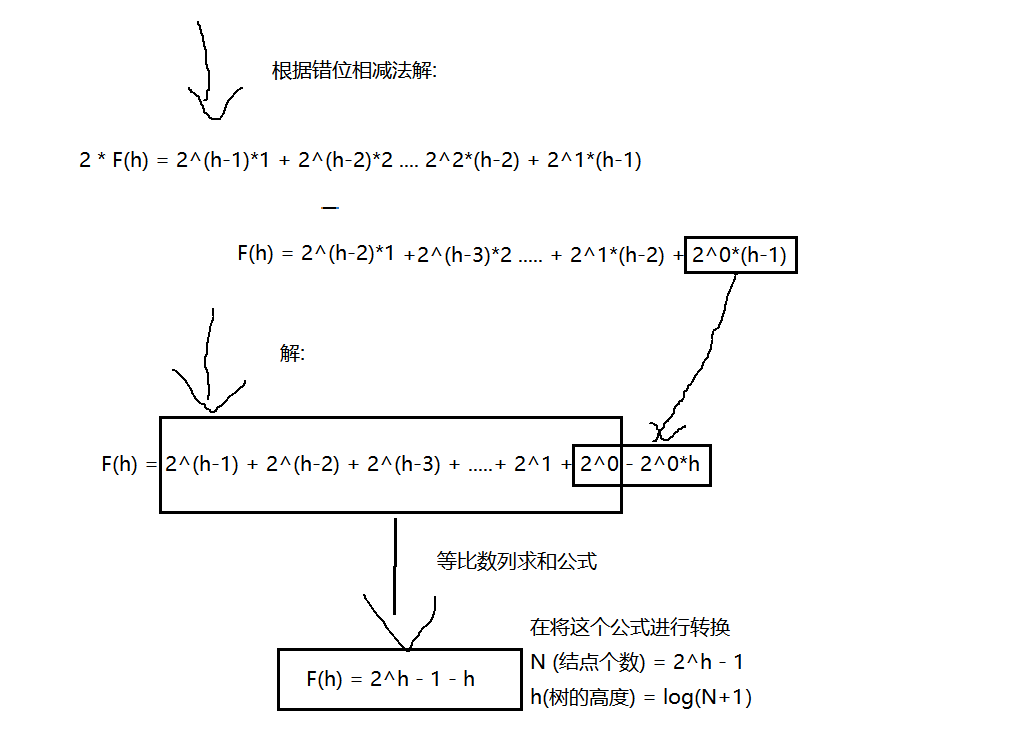
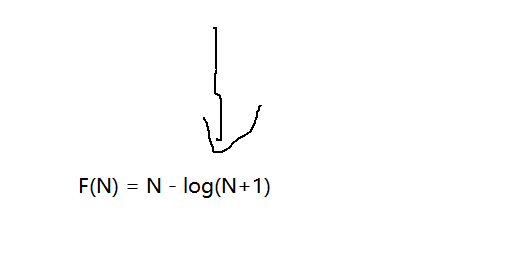
logN可以忽略不计, 所以向下调整时间复杂度为O(N)
接下来, 计算向上调整:
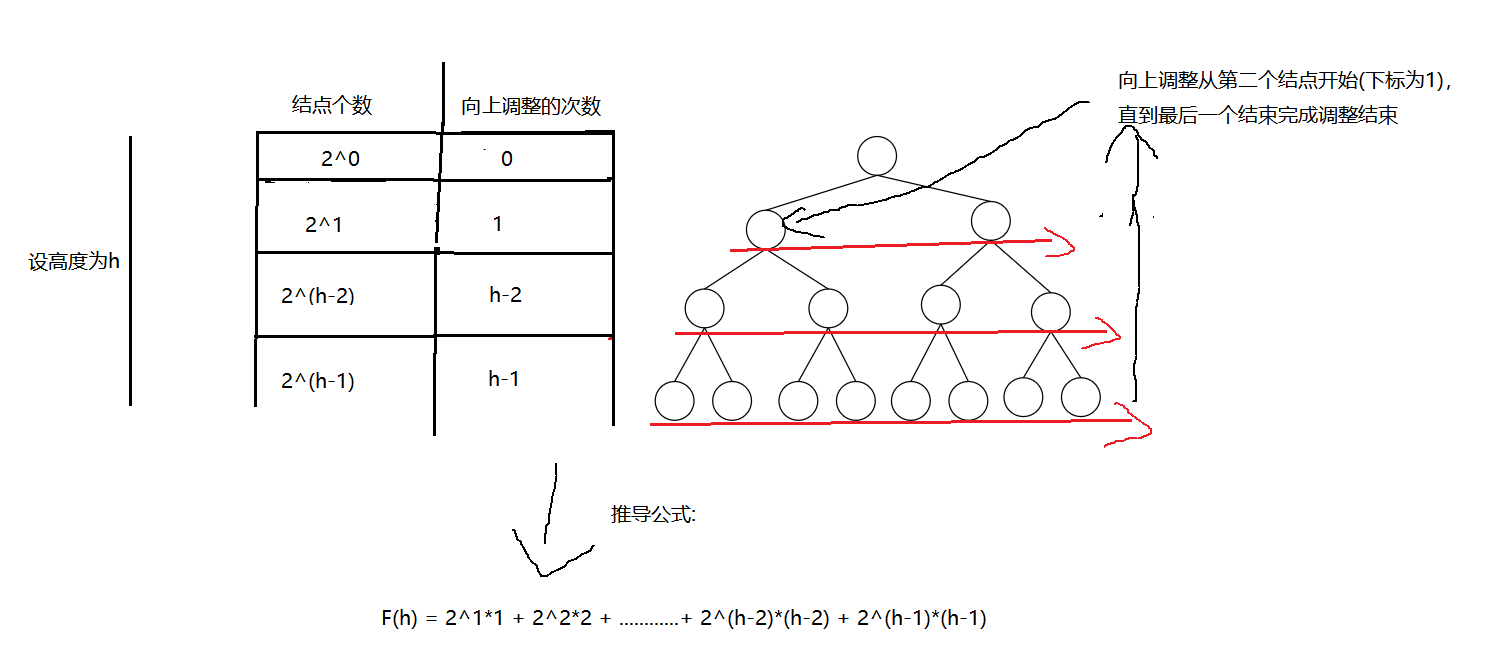
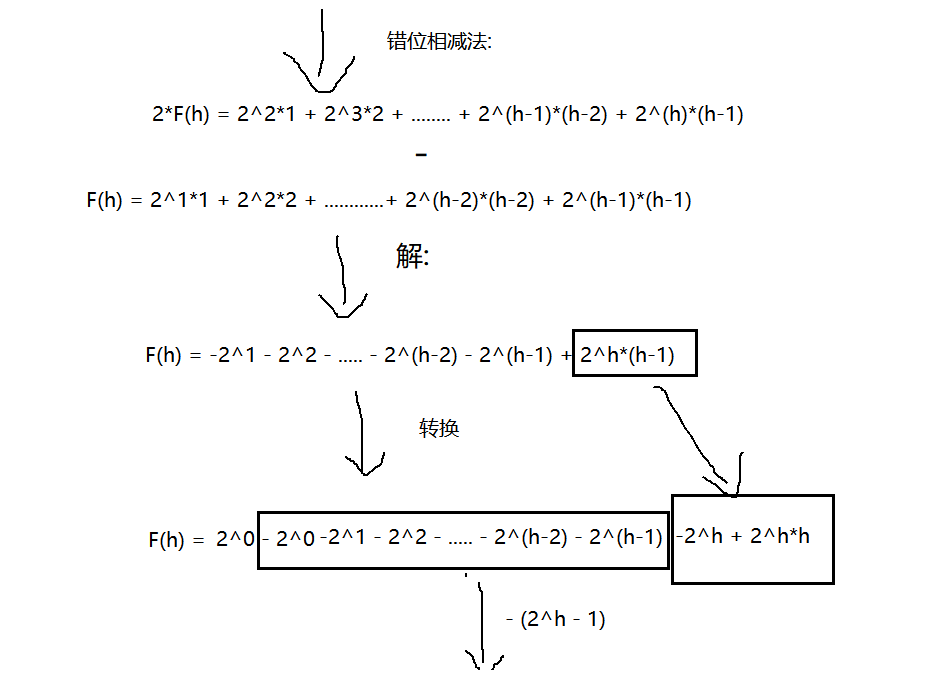

如图向上调整建堆, 时间复杂度为O(N*logN), 所以向下调整建堆效率更优
最后, 计算建堆后, 堆排序的时间复杂度
堆排序的时间复杂度

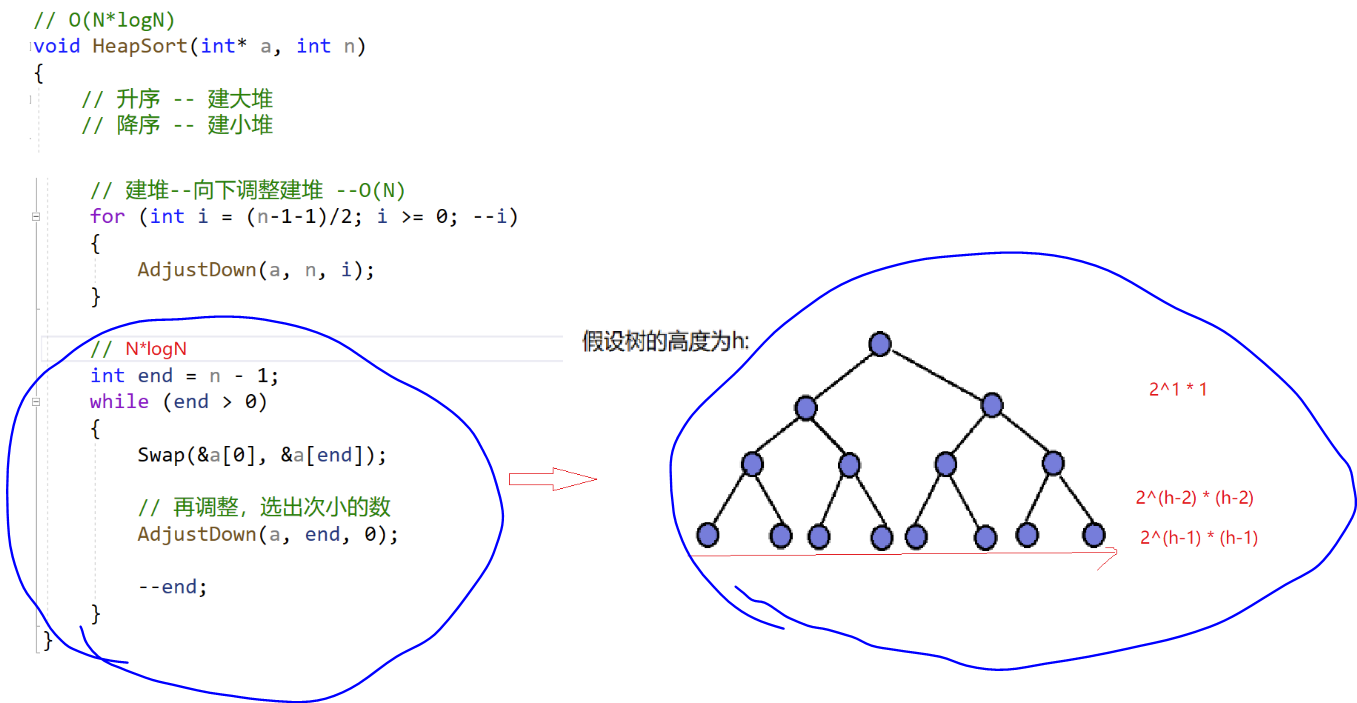
通过观察发现, 堆排序本质上和向上调整建堆相同
所以, 整个堆排序(建堆+排序)(N+N*log(N)), 在N*logN这一个量级





 浙公网安备 33010602011771号
浙公网安备 33010602011771号