复杂度
1. 复杂度概念
衡量一个算法的效率一般从时间和空间的角度
时间指一个算法执行所需要的时间,空间指执行算法所需要额外的空间, 在计算机科学中叫作时间和空间复杂度
2. 时间复杂度的计算
在复杂度概念中,写到时间复杂度指一个算法执行所需要的时间
那么,计算时间复杂度就是计算一个描述算法的程序,从编译链接最后生成可执行程序所花费的时间?
这个方法可行,但是有缺陷,比如有两个人A,B在比较算法效率,由于各自机器配置不同,就不能用时间去衡量
一个程序执行花费的时间与执行语句的数次成正比,所以计算程序执行花费的时间可以等于计算程序语句大概的执行次数
且执行次数与机器无关,比算法效率,比各自程序语句执行次数即可
// Func1中++count语句总共执行了多少次?
void Func1(int N)
{
int count = 0;
for (int i = 0; i < N ; ++ i)
{
for (int j = 0; j < N ; ++ j)
{
++count;
}
}
for (int k = 0; k < 2 * N ; ++ k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}Func1总共执行了 N2+ 2*N+10次语句
3. 大O渐近表示法
是否需要计算出准确的语句次数作为一个算法的时间复杂度?
实际上, 不需要计算出准确的执行次数, 只需要表示出属于哪一个量级,下面证明
// Func1中++count语句总共执行了多少次?
void Func1(int N)
{
int count = 0;
for (int i = 0; i < N ; ++ i)
{
for (int j = 0; j < N ; ++ j)
{
++count;
}
}
for (int k = 0; k < 2 * N ; ++ k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}Func1总共执行了 N2+ 2*N+10次语句
N = 10 , F(N) = 130
N = 100, F(N) = 10210
N = 1000, F(N) = 1002010
N越大, N2 的后两项对结果影响越小,当N无穷大时,后两项可以忽略不计
所以,Func1在N2 这一个量级 (当数据个数为100,语句执行1万次) ---> 用大O渐近表示法描述 ---> Func1的时间复杂度为 O(N2)
大O渐近表示法只是用来描述时间,空间效率属于哪一个量级
4. 计算时间复杂度实例
// 计算Func2的时间复杂度?
void Func2(int N)
{
int count = 0;
for (int k = 0; k < 2 * N ; ++ k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
printf("%d\n", count);
}Func2总执行 2*N+10 次语句 ---> 系数2, +10都可以忽略不计 ---> 时间复杂度为 O(N)
// 计算Func3的时间复杂度? N 远大于 M
void Func3(int N, int M)
{
int count = 0;
for (int k = 0; k < M; ++ k)
{
++count;
}
for (int k = 0; k < N ; ++ k)
{
++count;
}
printf("%d\n", count);
}Func3总执行 N+M次语句, 由于N远大于M, 所以M可以忽略不计 ---> 时间复杂度为 O(N)
// 计算Func4的时间复杂度?
void Func4(int N)
{
int count = 0;
for (int k = 0; k < 100; ++ k)
{
++count;
}
printf("%d\n", count);
}Func4总执行 100次语句, 100为常数, 大O渐近表示法规定执行常数次为1 ---> 时间复杂度为 O(1)
// 计算strchr的时间复杂度?
const char* strchr(const char* str, int character)
{
if (*str == character)
{
return str;
}
else
{
str++;
}
}strchr执行语句的次数可以等于查找的数次, 查找的次数等于N (字符串的长度)
最好情况: 查找1次找到 时间复杂度为 O(1),最坏情况: 查找N次找到时间复杂度为 O(N)
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
for (size_t i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
}
}
}
}首先需要理解冒泡排序思想
设数组5(N)个元素 [5,4,3,2,1]
第一次,排N-1次 [4, 3, 2, 1, 5]
第二次,排N-2次 [3, 2, 1, 4, 5]
........
排 2 次 [2, 1, 3, 4, 5]
排 1 次 [ 1, 2, 3, 4, 5]
这是一个等差数列, 根据等差数列求和公式 (首项+尾项)*项数/2 ---> (N-1+1)*N/2 ---> 时间复杂度为O(N2)
// 计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x)
{
int begin = 0;
int end = n - 1;
// [begin, end]:begin和end是左闭右闭区间,因此有=号
while (begin <= end)
{
int mid = begin + ((end - begin) >> 1);
if (a[mid] < x)
begin = mid + 1;
else if (a[mid] > x)
end = mid - 1;
else
return mid;
}
return -1;
}二分查找的次数的次数等于语句执行次数, 假设数组长度为N,x等于二分查找次数
2x = N ---> x = log2N ---> 时间复杂度为log2N
// 计算阶乘递归Fac的时间复杂度?
long long Fac(size_t N)
{
if(0 == N)
return 1;
return Fac(N-1)*N;
}语句执行的次数等于递归的次数 ---> 时间复杂度为O(N)

// 计算斐波那契递归Fib的时间复杂度?
long long Fib(size_t N)
{
if(N < 3)
return 1;
return Fib(N-1) + Fib(N-2);
}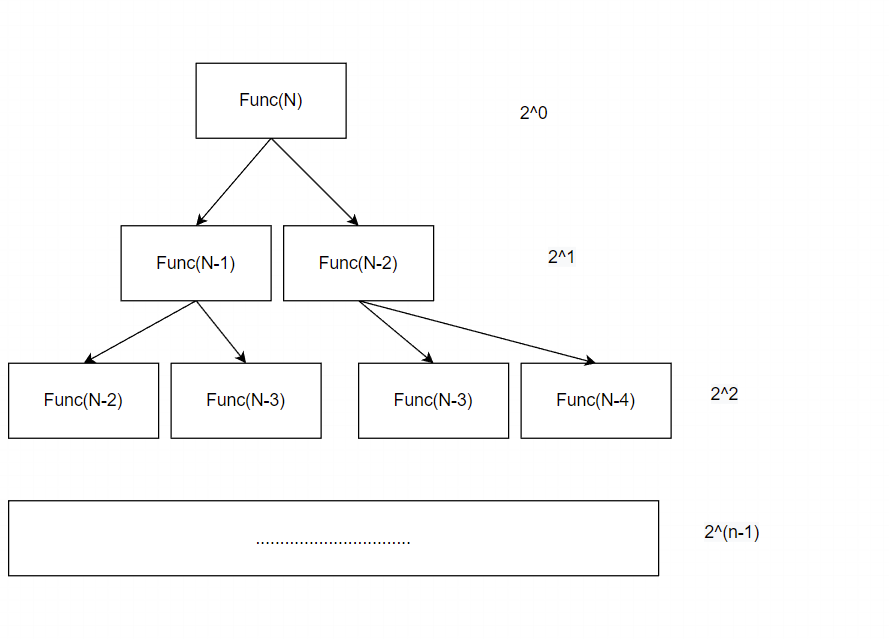
语句执行的次数等于递归的次数 ---> 时间复杂度为O(2N )
5. 计算空间复杂度
计算空间复杂度,计算的是创建变量的个数
除此之外,空间复杂度由函数在运行时创建的栈帧空间来确定
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i-1] > a[i])
{
Swap(&a[i-1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}创建了常数个变量,所以空间复杂度为 O(1)
// 计算Fibonacci的空间复杂度?
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{
if(n==0)
return NULL;
long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n ; ++i)
{
fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
}
return fibArray;
}动态开辟N+1个空间,空间复杂度为O(N)
注意,这个动态开辟的空间是为了执行这个斐波那契数列算法,上一个例子中的数组是数据源的提供, 计算空间复杂度计算的是执行算法所开辟额外空间
// 计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{
if(0 == N)
return 1;
return Fac(N-1)*N;
} 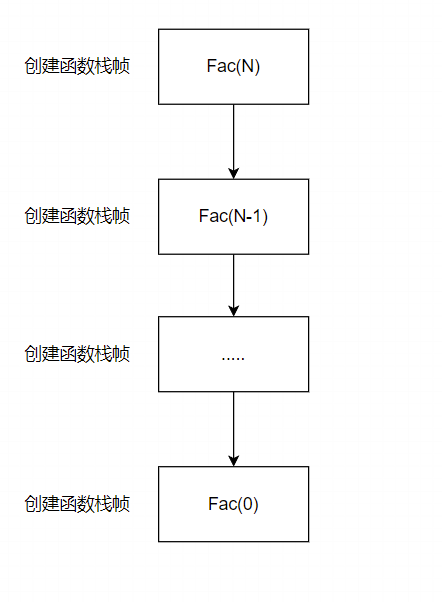
创建了N+1个函数栈帧空间, 空间复杂度为O(N)






 浙公网安备 33010602011771号
浙公网安备 33010602011771号