维比特算法

维比特算法（viterbi algorithm）算法可用于求解篱笆图（lattice，离散数学中的格）的最短路径问题。
算法的思路与多段图是类似的，将一个格分为多组的节点，图的节点按列组织，每列的节点数量可以不一样，每一列的节点只能和相邻列的节点相连，不能跨列相连，节点之间有着不同的距离，之后逐层迭代。

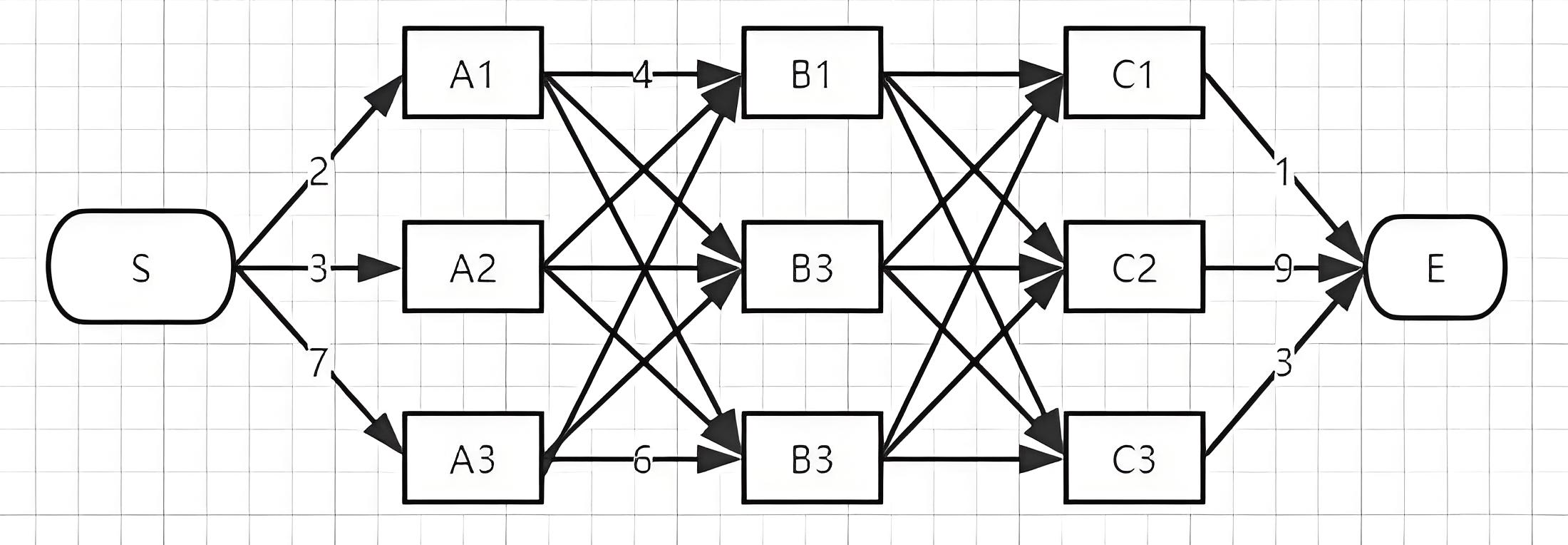
对于多段图算法中，我们可以求解出最短的距离的值，那么我们怎么知道最短路径具体是那一条呢。在维比特算法中的做法是，删除掉不可能是答案的路径，留下可能是答案的路径。
维比特算法是典型的动态规划算法，也就是说，我们在计算出最短路径之前，一定已经计算出了从起点到终点前一组节点的最短路径，所以我们只需要在计算部分最短路径时（子问题），删除掉经过该节点的非最短路径的边，因为假如最终的最短路径经过该点，那么起点到该店的最短路径一定是最终解的子路径，该点的非最短路径的边不可能是最终解的边。
例如，起点到B1点有三条路径S->A1->B1，S->A2->B1，S->A3->B1，经过计算可以发现S->A1->B1是起点到B1的最短路径，那么我们可以删除边A2->B1，A3->B1，以此类推，我们得到的状态转移方程如下：
假设Path[i]记录的是从起点到节点v[i]的最短路径，那么

Path[i]=min(Path[r]+cost(r,i))，其中（r,i）∈E（G）。
我们可以看出假如我们不删除不可能为最终解的边，也可以采用一个容器来记录起点到每一个点的最短路径。
综上，维比特算法中最经典的部分就是利用了解决子问题之后留下的解（用容器记录或者删除不可能的边），从而减少不必要的计算（相对于遍历所有可能路径的穷举法），降低时间复杂度，最短路径问题满足最优化原理和无后效性，即全局最优则局部也是最优。