阿里ranking loss优化ctr建模《Joint Optimization of Ranking and Calibration with Contextualized Hybrid Model》

背景

尽管 pairwise loss 和 listwise loss 相当于 pointwise loss 有更好的排序建模的能力，但是在CTR建模中一般还是使用的pointwise loss，主要是因为pointwise loss有更好的校准能力，其预估结果可以直接被视为点击概率。为了解决这个问题，阿里在这篇论文提出了联合优化排序和校准能力的方法（简称JRC）

 

方法

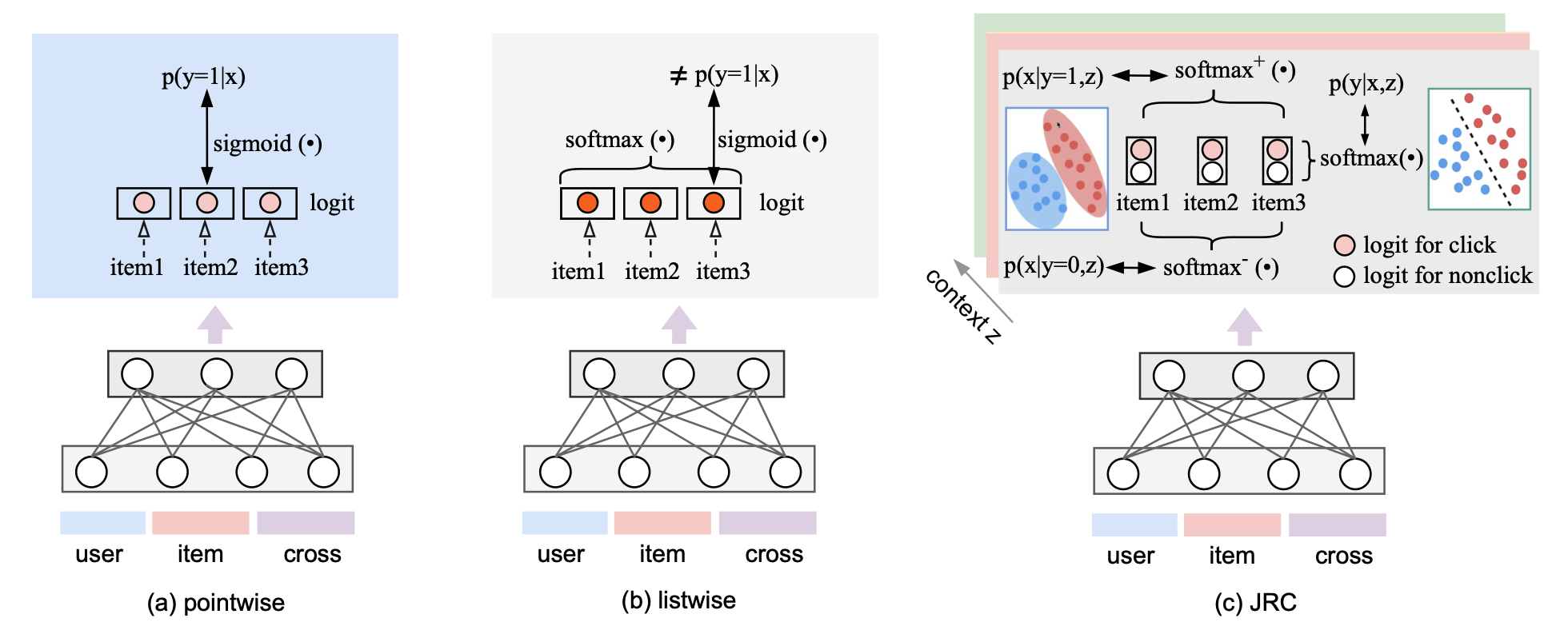
JRC采用了多任务建模的方式，包含两个目标：$f_{\theta}(\mathbf{x})[0]$建模nonclick-logit，$f_{\theta}(\mathbf{x})[1]$建模click-logit

用户点击概率可以表示为（对上面两个目标过softmax函数）：

$\hat{p}(y = 1|\mathbf{x}) = \dfrac{1}{1 + \exp\left(-\left(f_{\theta}(\mathbf{x})[1] - f_{\theta}(\mathbf{x})[0]\right)\right)}$

首先引入一个pointwise loss来保证校准能力：

$$ \begin{align*} \ell_{\text{calib}} &= -\sum_{\mathbf{x}, y} \log \hat{p}(y \mid \mathbf{x}) \\ &= -\sum_{\mathbf{x}, y} \log \frac{\exp(f_\theta(\mathbf{x})[y])}{\exp(f_\theta(\mathbf{x})[0]) + \exp(f_\theta(\mathbf{x})[1])} \end{align*} $$

然后，引入listwise loss来优化排序能力：

$$\ell_{\text{rank}} = -\sum_{\mathbf{x}, y, z} \log \frac{\exp(f_{\theta}(\mathbf{x})[y])}{\sum_{\mathbf{x}_i \in X_z} \exp(f_{\theta}(\mathbf{x}_i)[y])}$$

• 对每个正样本$(\boldsymbol{x}, y = 1)$，在相同的context $z$下，对比该正样本输出的click-logits和其他样本的click-logits，即：$\boldsymbol{f}_\theta(\boldsymbol{x})[1]$，使得该正样本的click-logits比其它样本的click-logits大。
• 对每个负样本$(\boldsymbol{x}, y = 0)$，在相同的context $\boldsymbol{z}$下，对比该负样本输出的nonclick-logits和其他样本的nonclick-logits，即：$\boldsymbol{f}_\theta(\boldsymbol{x})[0]$，使得该负样本的nonclick-logits比其它样本的nonclick-logits大。

最终的loss为两个loss的加权和：

\[ \ell_{\text{final}} = \alpha \ell_{\text{calib}} + (1 - \alpha) \ell_{\text{rank}} \]

 

参考资料

KDD'23 | 阿里, 排序和校准联合建模: 让listwise模型也能用于CTR预估