transfrom中的位置编码
transform为什么需要位置编码?
transform主要被引用在NLP任务中,对于任何一门语言,单词在句子中的位置以及排列顺序是非常重要的,不像RNN,transform本身没有捕获输入的单词的位置的能力,因此需要在输入时加上位置编码,让transform感受到输入单词的位置信息
怎么进行位置编码?
1. 用整型值标记位置
一种自然而然的想法是,给第一个token标记1,给第二个token标记2...,以此类推。
这种方法产生了以下几个主要问题:
(1)模型可能遇见比训练时所用的序列更长的序列,不利于模型的泛化。
(2)模型的位置表示是无界的。随着序列长度的增加,位置值会越来越大。
2. 用[0,1]范围标记位置
为了解决整型值带来的问题,可以考虑将位置值的范围限制在[0, 1]之内,其中,0表示第一个token,1表示最后一个token。比如有3个token,那么位置信息就表示成[0, 0.5, 1];若有四个token,位置信息就表示成[0, 0.33, 0.69, 1]。
但这样产生的问题是,当序列长度不同时,token间的相对距离是不一样的。例如在序列长度为3时,token间的相对距离为0.5;在序列长度为4时,token间的相对距离就变为0.33。
3. 用二进制向量标记位置
考虑到位置信息作用在input embedding上,因此比起用单一的值,更好的方案是用一个和input embedding维度一样的向量来表示位置。这时我们就很容易想到二进制编码。如下图,假设d_model = 3,那么我们的位置向量可以表示成:
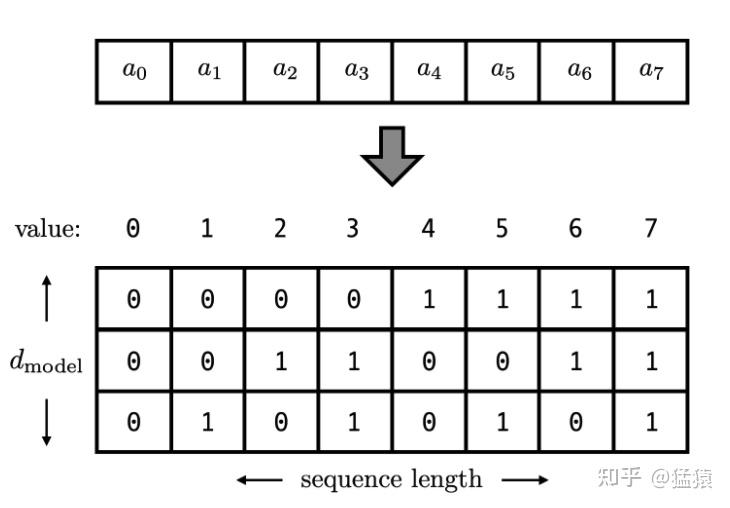
这下所有的值都是有界的(位于0,1之间),且transformer中的d_model本来就足够大,基本可以把我们要的每一个位置都编码出来了。
但是这种编码方式也存在问题:这样编码出来的位置向量,处在一个离散的空间中,不同位置间的变化是不连续的。假设d_model = 2,我们有4个位置需要编码,这四个位置向量可以表示成[0,0],[0,1],[1,0],[1,1]。我们把它的位置向量空间做出来:
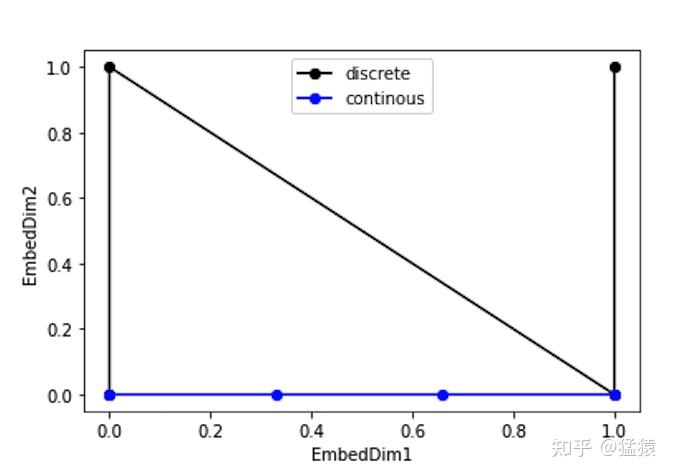
transform中的位置编码
定义:
- t是这个token在序列中的实际位置(例如第一个token为1,第二个token为2...)
- \(PE_t\in\mathbb{R}^d\) 是这个token的位置向量,\(PE_t^{(i)}\) 表示这个位置向量里的第i个元素
- \(d_{model}\) 是这个token的维度(在论文中,是512)
则 \(PE_t^{(i)}\) 可以表示为: \[ PE_t^{(i)}= \begin{cases} \sin(w_kt), & if\ i = 2k \\ \cos(w_kt), & if\ i = 2k + 1 \end{cases} \] 这里: \[ w_k = \frac{1}{10000^{2k/d_{model}}} \] \[ i = 0, 1, 2, 3, \dots, \frac{d_{model}}{2}-1 \]
可以看到,沿着向量维度从左到右,函数频率从高到低,波长从短到长,因此越往后的值越不敏感。采用频率为$w_k = \frac{1}{10000^{2k/d_{model}}}$的原因是因为sin/cos函数是周期函数,频率如果设的太小,可能会存在位置差距比较大的编码却距离很近
transform位置编码的性质
1. 相对位置表达能力
对于固定位置距离的k,PE(i+k)可以表示成PE(i)的线性函数。证明如下:
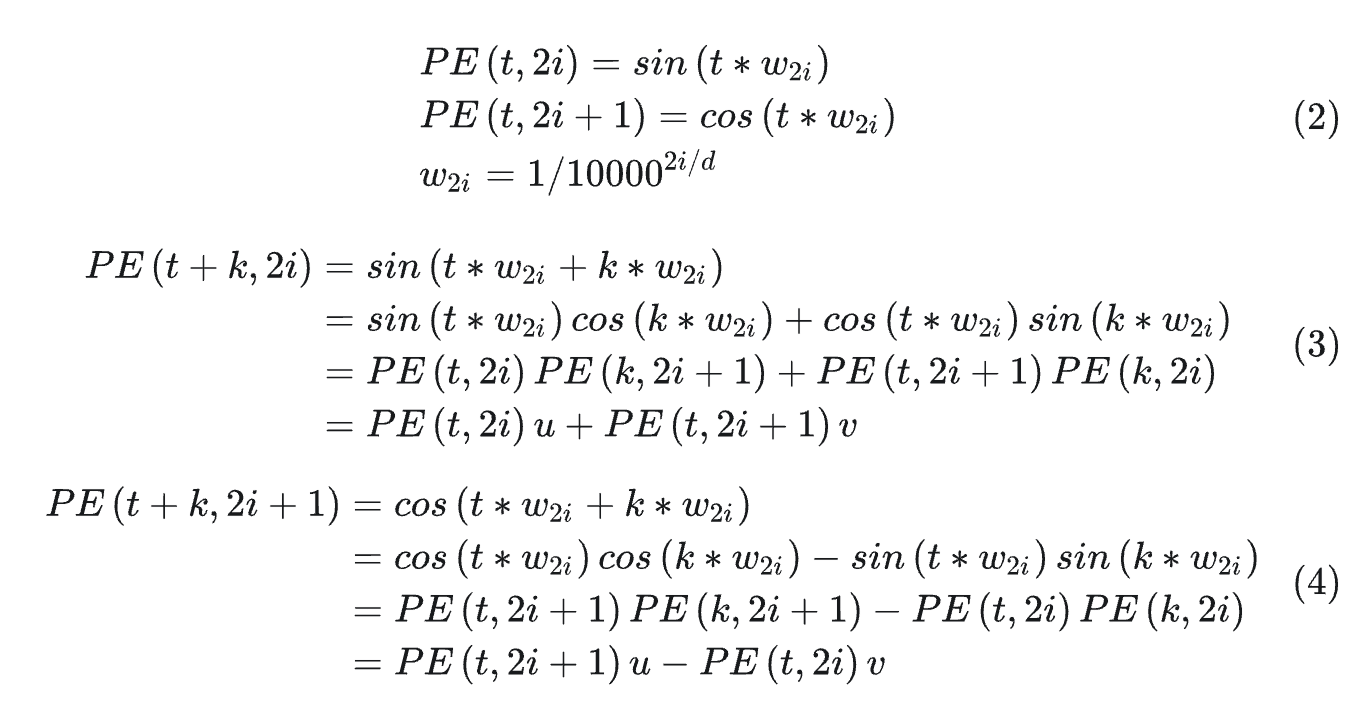
2. 内积只和相对位置 k 有关
Attention中的重要操作就是内积。计算两个位置的内积PE(t+k)PE(t)如下所示:
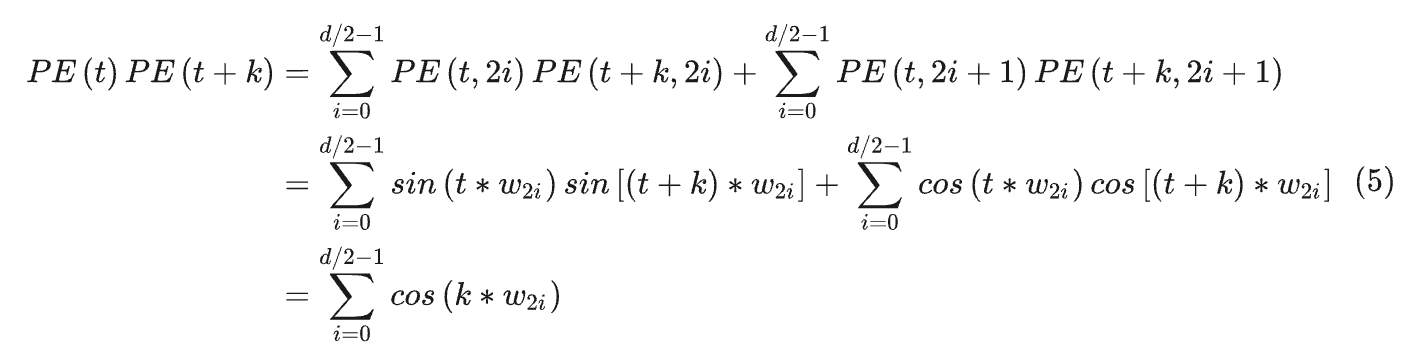
可以看到,最终的结果是关于k的一个常数。这表明两个位置向量的内积只和相对位置k有关。
通过计算,很容易得到PE(t+k)PE(t) = PE(t)PE(t-k),这表明编码具有对称性。
3. 远程衰减
可以发现,随着k的增加,位置向量的内积结果会逐渐降低,即会存在远程衰减。 如下图所示:
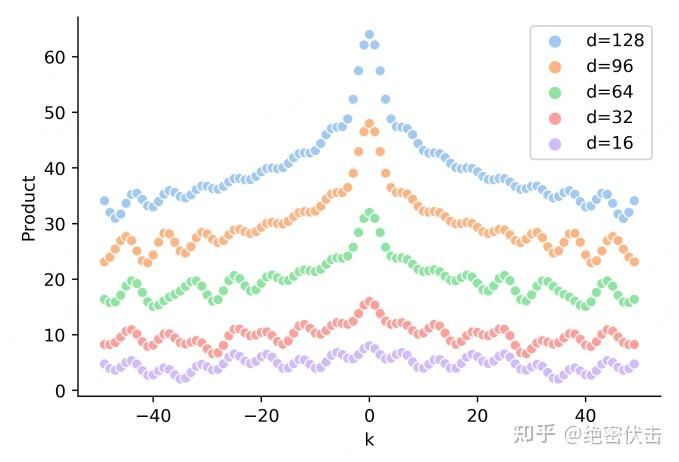
但是实际的Attention计算中还需要与attention的权重W相乘,即 $PE_t^T W_q^T W_k PE_{t + k}$ ,这时候内积的结果就不能反映相对距离,如下图所示:
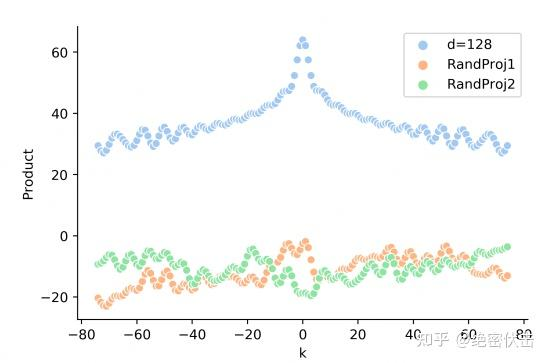
参考资料
Transformer学习笔记一:Positional Encoding(位置编码)




 浙公网安备 33010602011771号
浙公网安备 33010602011771号