策略梯度算法reinforce算法原理理解和代码实现
策略梯度算法
可以把t时刻开始的累积折扣奖励记为 Gt,代入上式得到:
\begin{align} \nabla \bar{R}_\theta \approx \frac{1}{N} \sum_{n = 1}^{N} \sum_{t = 1}^{T_n} G_t^n \nabla \log \pi_\theta \left( a_t^n \mid s_t^n \right) \end{align}
\begin{align} G_t &= \sum_{k = t + 1}^{T} \gamma^{k - t - 1} r_k \\ &= r_{t + 1} + \gamma G_{t + 1} \end{align}
算法流程

代码实现
下面我们来实现用REINFORCE 算法控制CartPole游戏,CartPole-v0`是OpenAI Gym库中一个经典的强化学习环境,属于控制类问题。
游戏描述
环境构成
状态空间
动作空间
奖励机制
目标
代码

import torch import torch.nn as nn import torch.optim as optim import torch.nn.functional as F import numpy as np import gym from torch.autograd import Variable import matplotlib.pyplot as plt import imageio # 折扣因子,用于计算折扣回报 GAMMA = 0.99 # 定义策略网络类,继承自nn.Module class PolicyNetwork(nn.Module): def __init__(self, num_inputs, num_actions, hidden_size, learning_rate=5e-4): # 调用父类的构造函数 super(PolicyNetwork, self).__init__() # 记录动作的数量 self.num_actions = num_actions # 定义第一个全连接层,输入维度为num_inputs,输出维度为hidden_size self.linear1 = nn.Linear(num_inputs, hidden_size) # 定义第二个全连接层,输入维度为hidden_size,输出维度为num_actions self.linear2 = nn.Linear(hidden_size, num_actions) # 定义Adam优化器,用于更新网络参数 self.optimizer = optim.Adam(self.parameters(), lr=learning_rate) def forward(self, x): # 通过第一个全连接层 x = self.linear1(x) # 使用ReLU激活函数 x = F.relu(x) # 通过第二个全连接层 x = self.linear2(x) # 使用Softmax函数将输出转换为动作概率分布 return F.softmax(x, dim=1) def get_action(self, state): # 将NumPy数组的状态转换为PyTorch张量,并添加一个维度以匹配网络输入要求 state = torch.from_numpy(state).float().unsqueeze(0) # 将状态包装为Variable(在较新版本的PyTorch中,Variable已可省略,但为了兼容旧代码保留) state = Variable(state) # 通过前向传播得到动作概率分布 probs = self.forward(state) # 将概率分布从PyTorch张量转换为NumPy数组,并去除多余的维度 probs_np = np.squeeze(probs.detach().numpy()) # 根据概率分布随机选择一个动作 action = np.random.choice(self.num_actions, p=probs_np) # 计算所选动作的对数概率 log_prob = torch.log(probs.squeeze(0)[action]) return action, log_prob def update_policy(self, rewards, log_probs): # 用于存储每个时间步的折扣回报 discounted_rewards = [] # 遍历每个时间步 for t in range(len(rewards)): # 初始化折扣回报 Gt = 0 # 初始化折扣幂次 pw = 0 # 从当前时间步开始,计算后续所有奖励的折扣回报 for r in rewards[t:]: Gt = Gt + GAMMA ** pw * r pw = pw + 1 # 将计算得到的折扣回报添加到列表中 discounted_rewards.append(Gt) # 将折扣回报列表转换为PyTorch张量 discounted_rewards = torch.tensor(discounted_rewards) # 对折扣回报进行标准化处理,减去均值并除以标准差 discounted_rewards = (discounted_rewards - discounted_rewards.mean()) / ( discounted_rewards.std() + 1e-9) # 用于存储每个时间步的策略梯度 policy_gradient = [] # 遍历每个时间步的对数概率和折扣回报 for log_prob, Gt in zip(log_probs, discounted_rewards): # 相当于最小化loss = -log_prob * Gt,通过深度学习框架自动优化 policy_gradient.append(-log_prob * Gt) # 清空优化器中的梯度信息 self.optimizer.zero_grad() # 将所有时间步的策略梯度堆叠成一个张量,并求和 policy_gradient = torch.stack(policy_gradient).sum() # 进行反向传播,计算梯度 policy_gradient.backward() # 使用优化器更新网络参数 self.optimizer.step() # 创建CartPole-v0环境,指定渲染模式为'rgb_array' env = gym.make('CartPole-v0', render_mode='rgb_array') # 初始化策略网络,输入维度为环境观测空间的维度4,输出维度为环境动作空间的维度2,隐藏层大小为128 policy_net = PolicyNetwork(env.observation_space.shape[0], env.action_space.n, 128) # 最大训练回合数 max_episode_num = 5000 # 每个回合的最大时间步数 max_steps = 1000 # 用于记录每个回合的步数 numsteps = [] # 用于记录每个回合的平均步数 avg_numsteps = [] # 用于记录每个回合的总奖励 all_rewards = [] # 开始训练循环 for episode in range(max_episode_num): # 重置环境,获取初始状态 state, _ = env.reset() # 用于存储每个时间步的动作对数概率 log_probs = [] # 用于存储每个时间步的奖励 rewards = [] # 在每个回合内进行时间步循环 for steps in range(max_steps): # 渲染环境,显示当前状态 env.render() # 根据当前状态获取动作和动作的对数概率 action, log_prob = policy_net.get_action(state) # 执行动作,获取新的状态、奖励、终止标志等信息 new_state, reward, done, _, _ = env.step(action) # 将动作的对数概率添加到列表中 log_probs.append(log_prob) # 将奖励添加到列表中 rewards.append(reward) # 如果环境达到终止条件 if done: # 调用更新策略的方法,更新网络参数 policy_net.update_policy(rewards, log_probs) break # 更新当前状态为新的状态 state = new_state # 计算当前回合的总奖励 total_reward = sum(rewards) all_rewards.append(total_reward) if episode % 100 == 0: print(f"Episode {episode}: Total Reward = {total_reward}") # 绘制训练损失曲线(使用总奖励曲线近似表示) plt.plot(all_rewards) plt.xlabel('Episode') plt.ylabel('Total Reward') plt.title('Training Loss Curve (Approximated by Total Reward)') plt.savefig('training_loss_curve.png') plt.show() # 最后运行一次游戏并保存效果图 frames = [] state, _ = env.reset() for steps in range(max_steps): frame = env.render() # 去掉mode参数 frames.append(frame) action, _ = policy_net.get_action(state) new_state, _, done, _, _ = env.step(action) if done: break state = new_state env.close() imageio.mimsave('game_play.gif', frames, fps=30)
reward训练曲线:
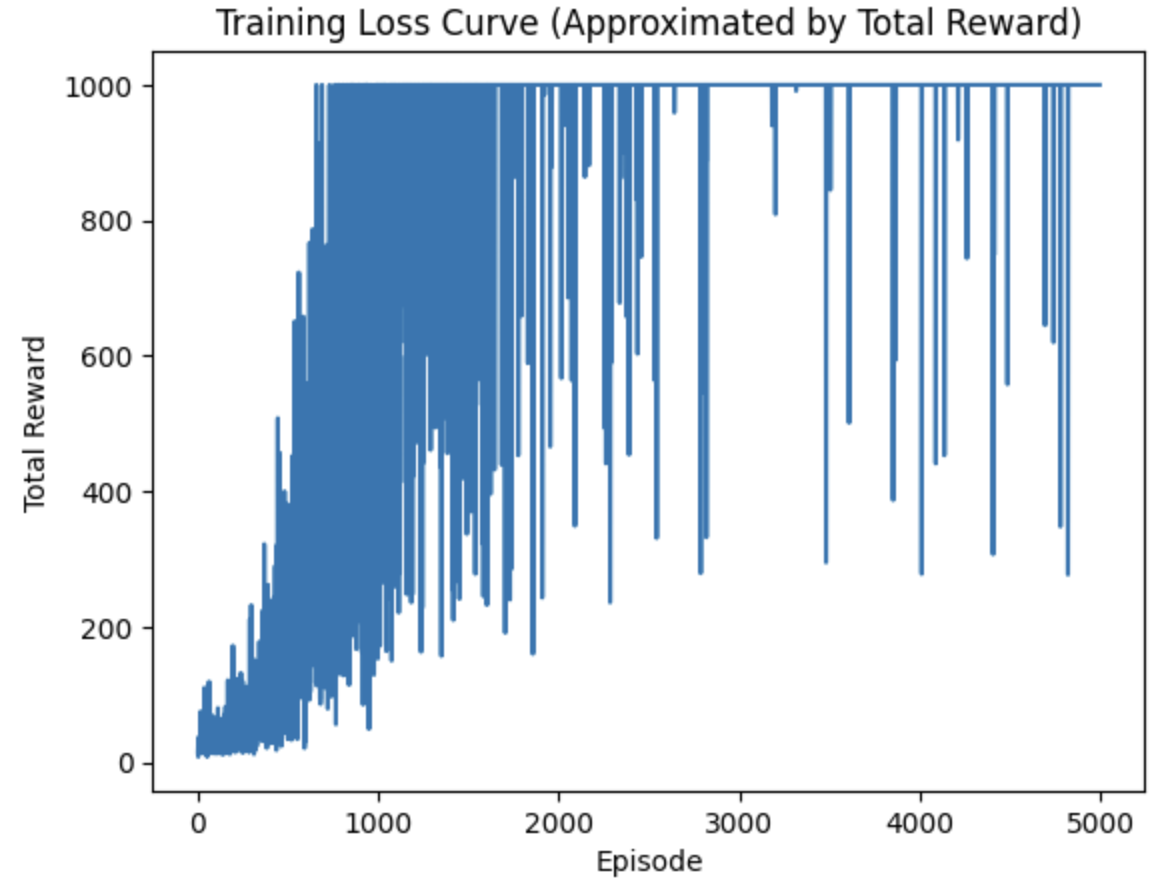
最终效果:
参考资料
从头理解策略梯度(Policy Gradient)算法及定理





 浙公网安备 33010602011771号
浙公网安备 33010602011771号