快手HoME多任务论文
论文链接:HoME: Hierarchy of Multi-Gate Experts for Multi-Task Learning at Kuaishou
背景
论文指出现在的MMOE/PLE等multitask模型存在以下几个问题:
- 专家崩溃:专家的输出分布存在显著差异,并且一些专家使用 ReLU 的零激活率超过 90%,使得门网络很难分配公平的权重来平衡专家
- 专家退化:一些共享专家只被一项任务占据,这表明共享专家失去了他们的能力,而是退化为一些特定专家
- 专家欠拟合(针对特定专家):在我们的服务中,我们有数十个行为任务需要预测,但我们发现一些数据稀疏的预测任务往往会忽略其特定专家,并为共享专家分配较大的权重。原因可能是共享专家可以从密集任务中感知更多的梯度更新和知识,而特定专家由于其稀疏行为很容易陷入欠拟合。
技术方案
Expert归一化和Swish机制
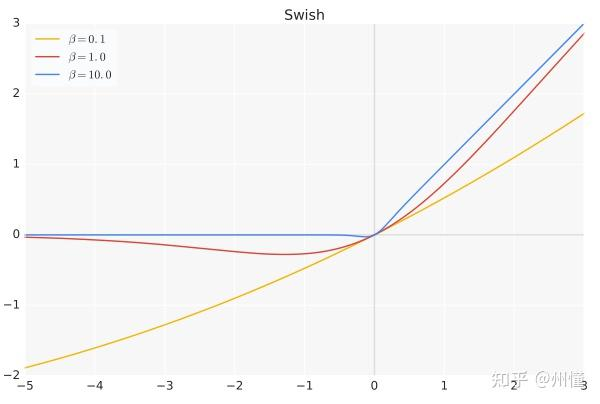
作者研究发现,造成专家崩溃的本质原因是因为不同专家输出尺度差异过大,为了解决问题,论文采用了在专家层之后加BN层,并把激活函数替换成Swish激活函数:
\[ \mathbf{z}_{norm} = \text{Batch_Normalization}(\mathbf{z}) = \gamma\frac{\mathbf{z} - \mu}{\sqrt{\delta^2 + \epsilon}} + \beta, \]
\[ \text{Swish}(x) = x \cdot \text{sigmoid}(\beta x) \]
DICE与BN之间的关联:
大家或许对DIN中的DICE函数还有印象,它的特点是可以根据数据的分布来自适应调整阶跃变化点,避免因数据的分布差异过大导致激活函数的值集中于0或1,先看其公式: \[ f(s)=p(s)\cdot s+(1 - p(s))\cdot\alpha s,\quad p(s)=\frac{1}{1 + e^{-\frac{s - E(s)}{\sqrt{Var(s)+\epsilon}}}} \] 一眼看去,p(s)不就是BN和sigmoid的结合体吗?我们再看一下BN的公式: \[ BN(s)=\gamma\frac{s - E(s)}{\sqrt{Var(s)+\epsilon}}+\beta \] 那么当BN中的平移缩放\(^\star\) (\(\beta,\gamma\))全部退化成最简易的形式(0,1),则有: \[ p(s)=sigmoid(BN(s)),\quad f(s)=sigmoid(BN(s))\cdot s+(1 - sigmoid(BN(s)))\cdot\alpha s \]
对比一下BN + Swish 和直接用Dice的区别:
BN+Swish:$f(s) = BN(s) \cdot \text{sigmoid}(BN(s))$
Dice:$f(s) = s \cdot p(s) = s \cdot \text{sigmoid}(BN(s)) + \alpha s \cdot (1 - \text{sigmoid}(BN(s)))$
层次掩码机制
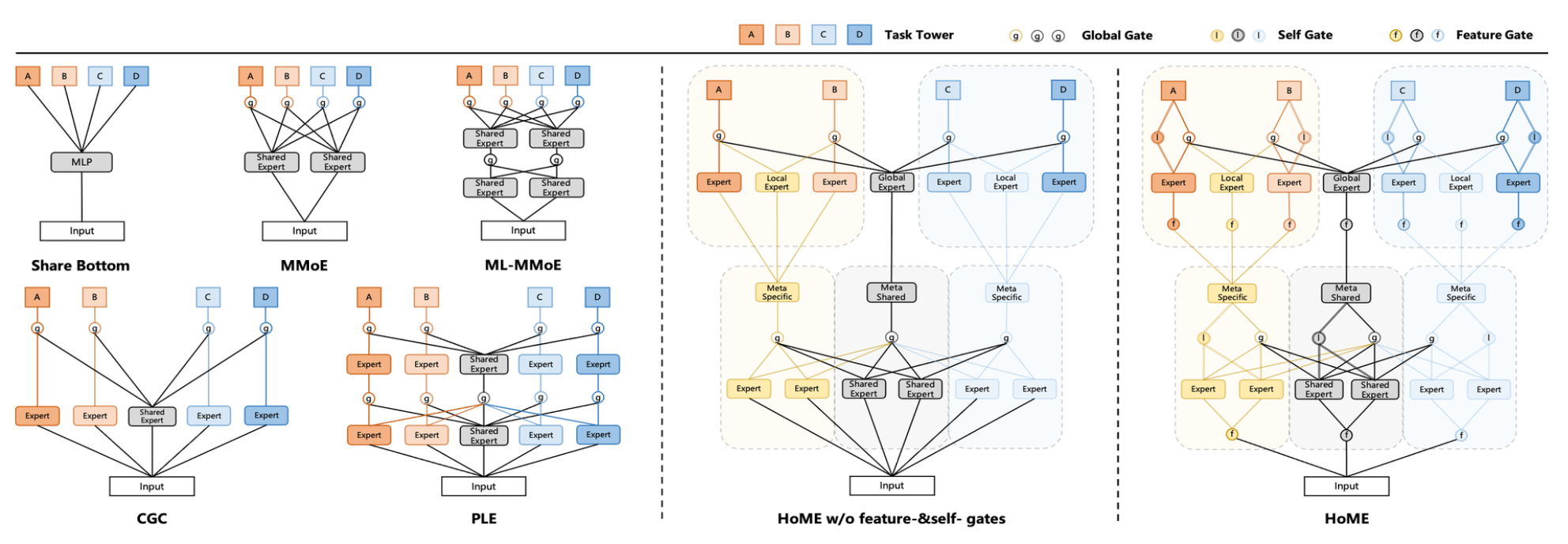
针对一些共享Expert退化成只起到私有Expert作用的情况, 作者提出基于任务相关性的先验知识来缓解这一问题,以快手短视频推荐为例, 预测任务可以大体分成两类:
- 被动观看的时长类任务: 如完播、长播、快划等
- 主动交互的互动类任务: 如点赞、评论、收藏等
更加这个划分,作者把模型分为两层:
- 第一层学习更粗粒度的表示,分别别提取:(1)时长子类别内共享知识;(2)全局共享知识; (3)互动子类目内共享知识
\[ \begin{align} \mathbf{z}_{meta}^{inter} &= \text{Sum}(\text{Gate}_{meta}^{inter}(\mathbf{v}), \{\text{Experts}_{meta}^{\{shared, inter\}}(\mathbf{v})\}), \\ \mathbf{z}_{meta}^{watch} &= \text{Sum}(\text{Gate}_{meta}^{watch}(\mathbf{v}), \{\text{Experts}_{meta}^{\{shared, watch\}}(\mathbf{v})\}), \\ \mathbf{z}_{meta}^{shared} &= \text{Sum}(\text{Gate}_{meta}^{shared}(\mathbf{v}), \{\text{Experts}_{meta}^{\{shared, inter, watch\}}(\mathbf{v})\}), \end{align} \]
- 第二层在第一层粗粒度表示基础上,进行正常的多任务预测,以点击率和有效播放两个目标为例, 第2阶段的过程描述如下:
\[ \begin{align} \hat{y}^{ctr} &= \text{Tower}^{ctr}\left(\text{Sum}\left(\text{Gate}^{ctr}\left(\mathbf{z}_{meta}^{inter} \oplus \mathbf{z}_{meta}^{shared}\right), \right.\right. \\ & \left.\left.\{\text{Experts}^{shared}\left(\mathbf{z}_{meta}^{shared}\right), \text{Experts}^{\{inter,ctr\}}\left(\mathbf{z}_{meta}^{inter}\right)\}\right)\right), \\ \hat{y}^{eotr} &= \text{Tower}^{eotr}\left(\text{Sum}\left(\text{Gate}^{eotr}\left(\mathbf{z}_{meta}^{watch} \oplus \mathbf{z}_{meta}^{shared}\right), \right.\right. \\ & \left.\left.\{\text{Experts}^{shared}\left(\mathbf{z}_{meta}^{shared}\right), \text{Experts}^{\{watch,eotr\}}\left(\mathbf{z}_{meta}^{watch}\right)\}\right)\right), \end{align} \]
Feature-gate与Self-gate机制
对于数据稀疏任务存在的Expert欠拟合的问题, 作者提出了两种门控机制来确保这些任务能够获得适当的梯度以最大化其有效性。
Feature-gate机制
对于feature-gate,其目的是为不同的任务专家生成不同的输入特征表示,以缓解所有专家共享相同的输入特征时的潜在梯度冲突
Self-gate机制
除了专家输入层面引入feature-gate,作者还在级联层次的各专家输出层面(包含第一层和第二层)添加了一个基于残差思想的self-gate, 比如上图所示的第二层级中, 红圈的I就表示self-gate。self-gaet是用于确保顶层梯度可以有效地传递到底层, 并只关注其特定专家的输出。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号