DIN（Deep Interest Network for Click-Through Rate Prediction）深度兴趣网络 论文阅读

背景

在广告或推荐中，用户的行为序列是一类非常重要的特征（如用户最近购买的商品序列），在以往的工作中我们一般是直接对序列特征求sumpooing（如下图base model），这个方案存在两个缺点：

1. 假设当前候选广告为上衣，用户的历史购买序列包含了裤子、帽子、洗衣机、电视等，直观上可以看出裤子和帽子和当前广告的相关性比较高，应该有更大权重。而普通sum pooling是等权的

2. 没有考虑到用户兴趣的变化，这个可以通过加入购买时间相关的特征来解决

DIN的模型结构如下图所示，DIN采用了attention的结构学习了候选广告和用户行为序列中不同物品的相似性权重，其实就是一种weighted-sum pooling方法

 

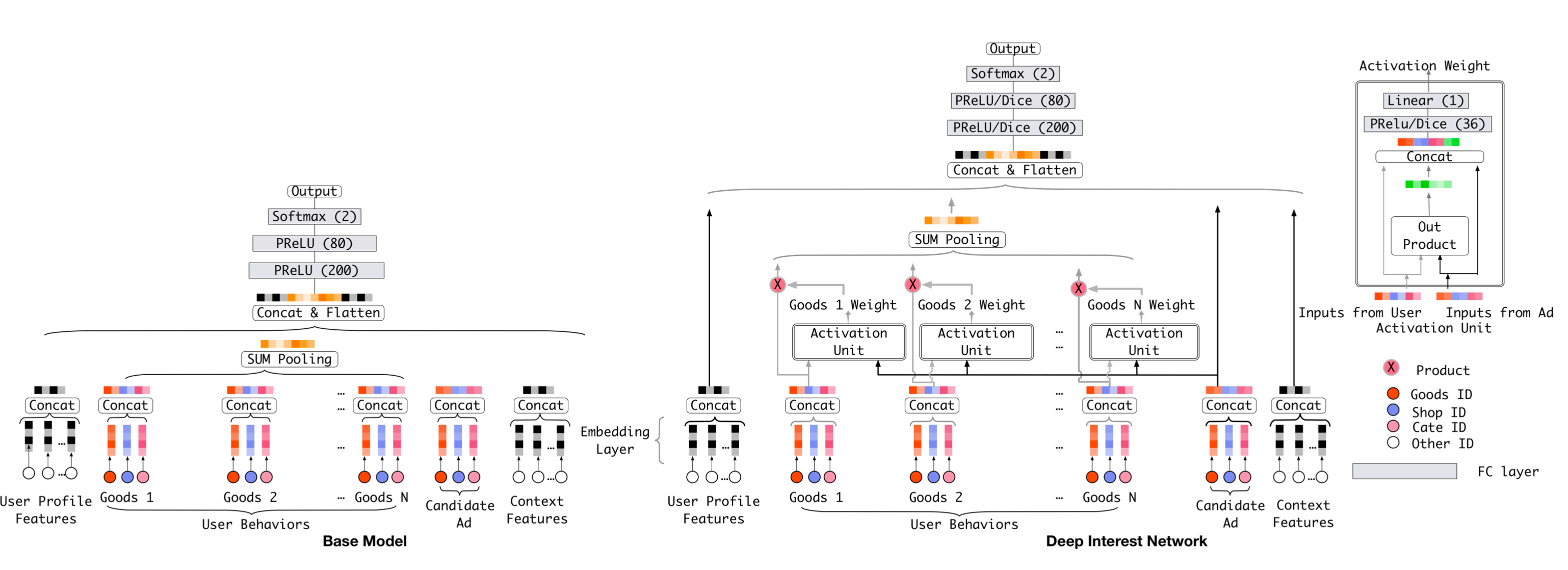
模型结构

DIN核心模型结构就是Activation Unit，其作用就是用来计算候选广告和用户行为序列物品的权重，最后求weighted-sum pooling，可以用下面公式表示：

\[ \boldsymbol{v}_{U}(A)=f(\boldsymbol{v}_{A},\boldsymbol{e}_{1},\boldsymbol{e}_{2},\ldots,\boldsymbol{e}_{H}) = \sum_{j = 1}^{H}a(\boldsymbol{e}_{j},\boldsymbol{v}_{A})\boldsymbol{e}_{j}=\sum_{j = 1}^{H}w_{j}\boldsymbol{e}_{j} \]

其中 \( \{ \boldsymbol{e}_{1}, \boldsymbol{e}_{2}, \ldots, \boldsymbol{e}_{H}\} \) 是用户 \( U \) 的行为嵌入向量列表，长度为 \( H \) ，\( \boldsymbol{v}_{A} \) 是候选广告 \( A \) 的嵌入向量。

注意：这里和self-attention不同，没有对权重过softmax归一化，论文给的解释是这样能更好的保留用户兴趣的强度

 

Mini-batch Aware Regularization

过拟合是工业网络训练面临的一个关键挑战。例如，随着细粒度特征的加入，比如维度达 6 亿的商品 ID 特征，在没有正则化的情况下，训练过程中第一个 epoch 之后模型性能就会迅速下降，直接将传统的正则化方法，如 L2 和 L1 正则化，应用于具有稀疏输入和数亿参数的训练网络是不现实的。以 L2 正则化为例。在基于随机梯度下降（SGD）的优化方法且无正则化的情况下，每个小批量中只需更新出现的非零稀疏特征的参数。然而，当加入 L2 正则化时，每个小批量都需要计算整个参数的 L2 范数，这会导致计算量极大，并且当参数规模达到数亿时是无法接受的。

因此，论文提出了 mini-batch aware regularization，它的主要思想是只对每个mini-batch中参数不为0的部分加L2正则，而不是对整个参数矩阵进行更新。这样可以避免对那些没有出现在mini-batch中的特征进行惩罚，从而保留更多的信息。此外，它还在一定程度上解决了数据长尾分布的过拟合问题。对长尾部分样本施加较大的惩罚而对短尾部分施加较小的惩罚来防止模型对于长尾部分的过拟合。

 

Dice 激活函数

PReLU是常用的激活函数

\[ f(s)=\begin{cases} s & \text{if } s > 0 \\ \alpha s & \text{if } s \leq 0. \end{cases} = p(s) \cdot s + (1 - p(s)) \cdot \alpha s, \]

其中：$p(s) = I(s > 0)$

Dice激活函数是一种改进的ReLU类激活函数，它的特点是可以根据数据的分布来自适应调整阶跃变化点，从而避免ReLU的死亡问题和不灵敏问题。它的定义如下：

\[ f(s) = p(s) \cdot s + (1 - p(s)) \cdot \alpha s, \quad p(s) = \frac{1}{1 + e^{-\frac{s - E[s]}{\sqrt{Var[s] + \epsilon}}}} \]

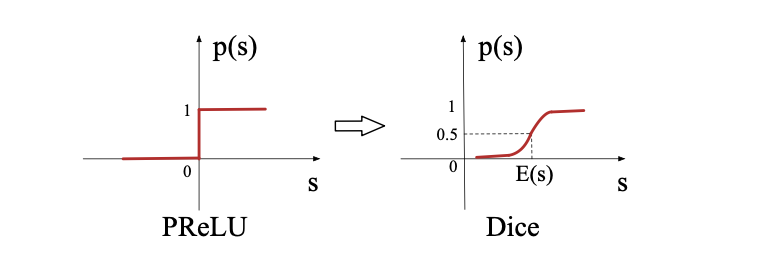
DICE函数理解：ps(x)函数相当于是BN + Sigmoid

 

模型实践

下面介绍实践中行为序列的构建和权重的计算步骤：

1. 构建长度为k的用户点击行为序列（序列中的每个商品用商品id、类别、行为时间等特征来表示（key），如果一个用户行为序列少于k，末尾用0填充）

2. 选取商品泛化特征来表示该商品（query）

3. tf.concat([query，key, query-key, query*key], axis=-1) 来计算候选商品和用户历史行为商品的相似性（权重），然后把这个权重经过几层nn后乘以用户历史行为商品特征的embedding，做weighted-sum pooling

 

代码实现

import tensorflow as tf
from tensorflow.keras import layers


class Dice(layers.Layer):
    def __init__(self):
        super(Dice, self).__init__()
        self.bn = layers.BatchNormalization(center=False, scale=False)
        self.alpha = self.add_weight(shape=(), initializer='zeros', trainable=True)

    def call(self, x):
        x_normed = self.bn(x)
        p = tf.sigmoid(x_normed)
        return p * x + (1 - p) * self.alpha * x


class Attention(layers.Layer):
    def __init__(self, hidden_units, use_softmax=False):
        super(Attention, self).__init__()
        self.dense_layer = tf.keras.Sequential()
        for units in hidden_units:
            self.dense_layer.add(layers.Dense(units, activation='sigmoid'))
        self.output_layer = layers.Dense(1)
        self.use_softmax = use_softmax

    def call(self, query, keys, keys_mask):
        # query: [batch_size, embedding_dim]
        # keys: [batch_size, max_length, embedding_dim]
        # keys_mask: [batch_size, max_length]
        query = tf.tile(tf.expand_dims(query, 1), [1, tf.shape(keys)[1], 1])  # [batch_size, max_length, embedding_dim]
        inputs = tf.concat([query, keys, query - keys, query * keys], axis=-1)
        outputs = self.dense_layer(inputs)
        scores = self.output_layer(outputs)  # [batch_size, max_length, 1]
        scores = tf.squeeze(scores, axis=-1)  # [batch_size, max_length]

        # 应用掩码
        paddings = tf.ones_like(scores) * (-2 ** 32 + 1)
        scores = tf.where(keys_mask, scores, paddings)

        if self.use_softmax:
            scores = tf.nn.softmax(scores)  # [batch_size, max_length]
        output = tf.reduce_sum(keys * tf.expand_dims(scores, -1), axis=1)  # [batch_size, embedding_dim]
        return output


class DIN(tf.keras.Model):
    def __init__(self, user_feature_dim, item_feature_dim, embedding_dim, hidden_units, attention_hidden_units):
        super(DIN, self).__init__()
        self.user_embedding = layers.Embedding(user_feature_dim, embedding_dim)
        self.item_embedding = layers.Embedding(item_feature_dim, embedding_dim)
        self.attention = Attention(attention_hidden_units)
        self.dense_layer = tf.keras.Sequential()
        for units in hidden_units:
            self.dense_layer.add(layers.Dense(units))
            self.dense_layer.add(Dice())
        self.output_layer = layers.Dense(1, activation='sigmoid')

    def call(self, user_features, item_features, hist_item_features, hist_mask):
        user_emb = self.user_embedding(user_features)  # [batch_size, embedding_dim]
        item_emb = self.item_embedding(item_features)  # [batch_size, embedding_dim]
        hist_item_embs = self.item_embedding(hist_item_features)  # [batch_size, max_length, embedding_dim]

        hist_attention_emb = self.attention(item_emb, hist_item_embs, hist_mask)  # [batch_size, embedding_dim]

        inputs = tf.concat([user_emb, item_emb, hist_attention_emb], axis=-1)
        outputs = self.dense_layer(inputs)
        output = self.output_layer(outputs)
        return output


# 示例使用
user_feature_dim = 100
item_feature_dim = 200
embedding_dim = 16
hidden_units = [32, 16]
attention_hidden_units = [32, 16]

model = DIN(user_feature_dim, item_feature_dim, embedding_dim, hidden_units, attention_hidden_units)

# 模拟输入数据
batch_size = 32
user_features = tf.random.uniform([batch_size], minval=0, maxval=user_feature_dim, dtype=tf.int32)
item_features = tf.random.uniform([batch_size], minval=0, maxval=item_feature_dim, dtype=tf.int32)
max_length = 10
hist_item_features = tf.random.uniform([batch_size, max_length], minval=0, maxval=item_feature_dim, dtype=tf.int32)
real_length = tf.random.uniform([batch_size], minval=0, maxval=max_length, dtype=tf.int32)
hist_mask = tf.random.uniform([batch_size, max_length], minval=0, maxval=2, dtype=tf.int32) > 0

# 前向传播
output = model(user_features, item_features, hist_item_features, hist_mask)
print("Output shape:", output.shape)