常用激活函数

Sigmoid

$\sigma \left( z \right) = \frac{1}{{1 + {e^{ - z}}}}$，${\sigma ^`}\left( z \right) = \sigma \left( z \right)\left( {1 - \sigma \left( z \right)} \right)$

优点：求导容易，单调连续，输出范围在0到1之间。

缺点：导数小于0.25，在大部分区间都饱和，容易造成梯度消失。

 

tanh

$\tanh \left( z \right) = \frac{{{e^z} - {e^{ - z}}}}{{{e^z} + {e^{ - z}}}} = 2sigmoid\left( {2z} \right) - 1$，${t^`}\left( z \right) = 1 - {\left( {t\left( z \right)} \right)^2}$

优点：比sigmoid收敛快，在0附近近似为线性，以0为中心。

缺点：梯度小于等于1，还是容易造成梯度消失。

 

ReLU

$ReLU\left( z \right) = \max \left( {0,z} \right)$

优点：大于0部分梯度恒为1，不容易造成梯度消失和梯度爆炸，收敛速度快，提供了网络的稀疏表达能力，能减少过拟合

缺点：可能会造成神经元死亡，输出非平滑，在0处不可导，输出不是以0为中心的，可能导致后续层输入分布偏移（需 Batch Normalization 缓解）

 

PReLU

\[ f(x) = \begin{cases} x, & \text{当 } x \geq 0 \\ \alpha x, & \text{当 } x < 0 \end{cases} \]

其中，\(\alpha\) 是一个可学习的参数（通常初始化为一个较小的正数，如0.01），用于控制负区间的斜率

• 当 \(\alpha = 0\) 时，PReLU退化为标准ReLU
• 当 \(\alpha\) 为固定值（如0.25）时，称为Leaky ReLU
• 当 \(\alpha\) 由模型自动学习时，即为PReLU

 

softplus

$softplus\left( z \right) = \ln \left( {1 + {e^z}} \right)$

优点：输出平滑，不会造成神经元死亡

缺点：计算复杂度高，梯度小于1，收敛速度慢，输出不是以0为中心的，可能导致后续层输入分布偏移（需 Batch Normalization 缓解）

 

softmax

$soft\max \left( {{z_i}} \right) = \frac{{{e^{{z_i}}}}}{{\sum\limits_{j = 1}^n {{e^{{z_j}}}} }}$，$\frac{{\partial {S_i}}}{{{z_j}}} = \left\{ {\begin{array}{*{20}{c}}
{{S_i}\left( {1 - {S_j}} \right),i = j}\\
{ - {S_j}{S_i},i \ne j}
\end{array}} \right.$

softmax并不会改变输出层的相对大小，所以为了减少计算量，神经网络在推理阶段一般不会计算softmax值，只在学习阶段计算softmax值。

 

Swish

 \[ \text{Swish}(x) = x \cdot \sigma(x) \]

其中 \( \sigma(x) = \frac{1}{1 + e^{-x}} \) 是Sigmoid函数

导数公式： \[ \text{Swish}'(x) = \text{Swish}(x) + \sigma(x) \cdot (1 - \text{Swish}(x)) \]

或简化为： \[ \text{Swish}'(x) = \sigma(x) + x \cdot \sigma(x) \cdot (1 - \sigma(x)) \] 

优点：相比于ReLU函数来说，Swish整体平滑可导，并且避免了在小于0的区间内神经元死亡的现象，精度更高

缺点：计算复杂度更高

 

 

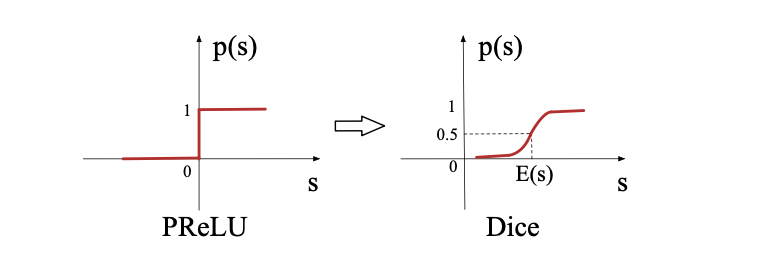
Dice

Dice激活函数是一种改进的ReLU类激活函数，它的特点是可以根据数据的分布来自适应调整阶跃变化点，从而避免ReLU的死亡问题和不灵敏问题。它的定义如下：

\[ f(s) = p(s) \cdot s + (1 - p(s)) \cdot \alpha s, \quad p(s) = \frac{1}{1 + e^{-\frac{s - E[s]}{\sqrt{Var[s] + \epsilon}}}} \]

DICE函数理解：ps(x)函数相当于是BN + Sigmoid

class Dice(nn.Module):
    def __init__(self, dim):
        super().__init__()
        self.bn = nn.BatchNorm1d(dim, eps=1e-9)
        self.alpha = nn.Parameter(torch.zeros(1))
        
    def forward(self, x):
        x_normed = self.bn(x)
        p = torch.sigmoid(x_normed)
        return p * x + (1 - p) * self.alpha * x

 

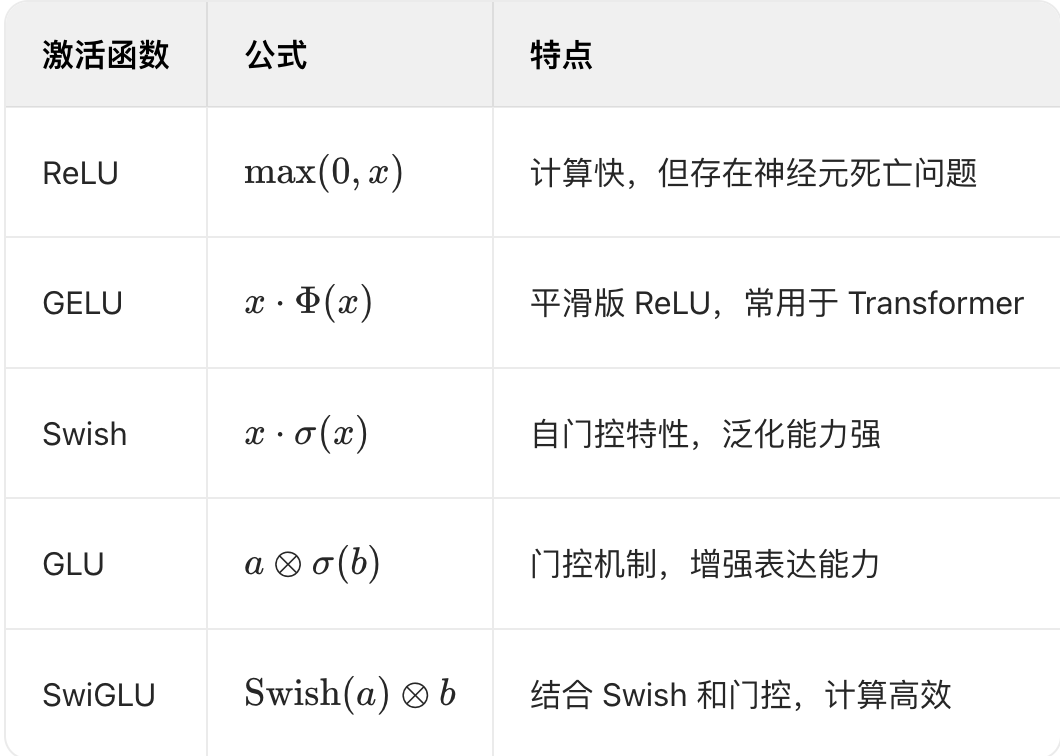
SwiGLU

\(\text{SwiGLU}(x, W, V, b, c) = \text{Swish}_\beta(xW + b) \otimes (xV + c)\) 其中：

• x 是输入向量；
• W 和 V 是权重矩阵；
• b 和 c 是偏置项；
• \(\text{Swish}_\beta(x) = x \cdot \sigma(\beta x)\)，\(\beta\) 是可学习参数或固定值（通常为 1）。

优点：

• 通过门控机制，SwiGLU 能选择性地激活神经元，捕获更复杂的模式；
• Swish 函数（\(x \cdot \sigma(x)\)）结合了线性和非线性特性，缓解了梯度消失问题。

应用场景：

在大型语言模型（如 PaLM、GPT-4）中，SwiGLU 常被用于替换传统的前馈网络（FFN）

 

 

参考资料

深度学习中激活函数总结

深度学习中Batch Normalization和Dice激活函数