分类算法--决策树算法
一.什么是分类算法
分类(Categorization or Classification)就是按照某种标准给对象贴标签(label),再根据标签来区分归类。
分类是事先定义好类别 ,类别数不变 。分类器需要由人工标注的分类训练语料训练得到,属于有指导学习范畴。
二.决策树算法
1.概述
决策树(decision tree)——是一种被广泛使用的分类算法。
相比贝叶斯算法,决策树的优势在于构造过程不需要任何领域知识或参数设置
在实际应用中,对于探测式的知识发现,决策树更加适用。
2.算法思想
通俗来说,决策树分类的思想类似于找对象。现想象一个女孩的母亲要给这个女孩介绍男朋友,于是有了下面的对话:
女儿:多大年纪了?
母亲:26。
女儿:长的帅不帅?
母亲:挺帅的。
女儿:收入高不?
母亲:不算很高,中等情况。
女儿:是公务员不?
母亲:是,在税务局上班呢。
女儿:那好,我去见见。
这个女孩的决策过程就是典型的分类树决策。
实质:通过年龄、长相、收入和是否公务员对将男人分为两个类别:见和不见
假设这个女孩对男人的要求是:30岁以下、长相中等以上并且是高收入者或中等以上收入的公务员,那么这个可以用下图表示女孩的决策逻辑
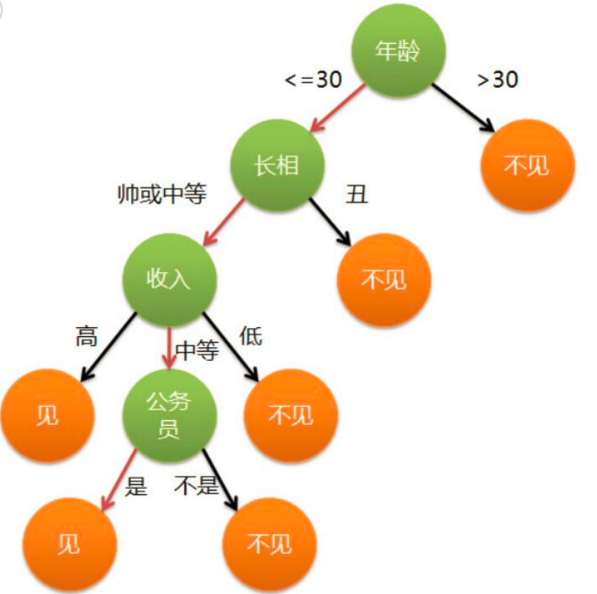
上图完整表达了这个女孩决定是否见一个约会对象的策略,其中:
◊绿色节点表示判断条件
◊橙色节点表示决策结果
◊箭头表示在一个判断条件在不同情况下的决策路径
图中红色箭头表示了上面例子中女孩的决策过程。
这幅图基本可以算是一颗决策树,说它“基本可以算”是因为图中的判定条件没有量化,如收入高中低等等,还不能算是严格意义上的决策树,如果将所有条件量化,则就变成真正的决策树了。
决策树分类算法的关键就是根据“先验数据”构造一棵最佳的决策树,用以预测未知数据的类别
决策树:是一个树结构(可以是二叉树或非二叉树)。其每个非叶节点表示一个特征属性上的测试,每个分支代表这个特征属性在某个值域上的输出,而每个叶节点存放一个类别。使用决策树进行决策的过程就是从根节点开始,测试待分类项中相应的特征属性,并按照其值选择输出分支,直到到达叶子节点,将叶子节点存放的类别作为决策结果。
3.决策树的构造
不同于贝叶斯算法,决策树的构造过程不依赖领域知识,它使用属性选择度量来选择将元组最好地划分成不同的类的属性。所谓决策树的构造就是进行属性选择度量确定各个特征属性之间的拓扑结构。
构造决策树的关键步骤是分裂属性。所谓分裂属性就是在某个节点处按照某一特征属性的不同划分构造不同的分支,其目标是让各个分裂子集尽可能地“纯”。尽可能“纯”就是尽量让一个分裂子集中待分类项属于同一类别。分裂属性分为三种不同的情况:
1、属性是离散值且不要求生成二叉决策树。此时用属性的每一个划分作为一个分支。
2、属性是离散值且要求生成二叉决策树。此时使用属性划分的一个子集进行测试,按照“属于此子集”和“不属于此子集”分成两个分支。
3、属性是连续值。此时确定一个值作为分裂点split_point,按照>split_point和<=split_point生成两个分支。
构造决策树的关键性内容是进行属性选择度量,属性选择度量是一种选择分裂准则,是将给定的类标记的训练集合的数据划分D“最好”地分成个体类的启发式方法,它决定了拓扑结构及分裂点split_point的选择。
属性选择度量算法有很多,一般使用自顶向下递归分治法,并采用不回溯的贪心策略。这里介绍ID3和C4.5两种常用算法。
3.1.ID3算法
ID3算法最早是由罗斯昆(J. Ross Quinlan)于1975年在悉尼大学提出的一种分类预测算法,算法以信息论为基础,其核心是“信息熵”。ID3算法通过计算每个属性的信息增益,认为信息增益高的是好属性,每次划分选取信息增益最高的属性为划分标准,重复这个过程,直至生成一个能完美分类训练样例的决策树。

3.1 ID3算法与决策树的流程
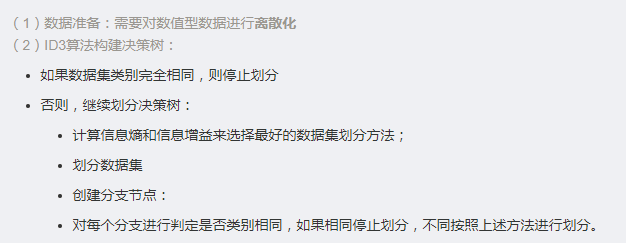
3.1.2 python实现ID3算法
1.创建 trees.py文件,在其中创建构建决策树的函数。
首先构建一组测试数据:
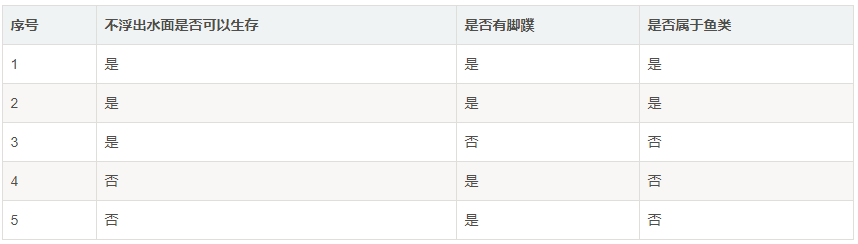
2.创建trees.py文件
#1.构造决策树数据 def createDataSet(): ''' 构造决策树数据 :return: ''' dataSet=[[1,1,'yes'],[1,1,'yes'],[1,0,'no'],[0,1,'no'],[0,1,'no']] labels=['no surfacing','flippers'] return dataSet,labels #2.计算香农熵 from math import log def calcShannonEnt(dataSet): ''' 计算香农熵 :param dataSet: :return: ''' numEntries = len(dataSet) #nrows #为所有的分类类目创建字典 labelCounts ={} for featVec in dataSet: currentLable=featVec[-1] #取得最后一列数据 if currentLable not in labelCounts.keys(): labelCounts[currentLable]=0 labelCounts[currentLable]+=1 #计算香农熵 shannonEnt=0.0 for key in labelCounts: prob = float(labelCounts[key]) / numEntries shannonEnt -= prob * log(prob, 2) return shannonEnt #3.按照最大信息增益划分数据集 #定义按照某个特征进行划分的函数splitDataSet #输入三个变量(待划分的数据集,特征,分类值) def splitDataSet(dataSet,axis,value): retDataSet=[] for featVec in dataSet: if featVec[axis]==value : reduceFeatVec=featVec[:axis] reduceFeatVec.extend(featVec[axis+1:]) retDataSet.append(reduceFeatVec) return retDataSet #返回不含划分特征的子集 #定义按照最大信息增益划分数据的函数 def chooseBestFeatureToSplit(dataSet): numFeature=len(dataSet[0])-1 baseEntropy=calcShannonEnt(dataSet)#香农熵 bestInforGain=0 bestFeature=-1 for i in range(numFeature): featList=[number[i] for number in dataSet] #得到某个特征下所有值(某列) uniqualVals=set(featList) #set无重复的属性特征值 newEntropy=0 for value in uniqualVals: subDataSet=splitDataSet(dataSet,i,value) prob=len(subDataSet)/float(len(dataSet)) #即p(t) newEntropy+=prob*calcShannonEnt(subDataSet)#对各子集香农熵求和 infoGain=baseEntropy-newEntropy #计算信息增益 #最大信息增益 if (infoGain>bestInforGain): bestInforGain=infoGain bestFeature=i return bestFeature #返回特征值 #4.创建决策树构造函数createTree import operator #投票表决代码 def majorityCnt(classList): classCount={} for vote in classList: if vote not in classCount.keys():classCount[vote]=0 classCount[vote]+=1 sortedClassCount=sorted(classCount.items,key=operator.itemgetter(1),reversed=True) return sortedClassCount[0][0] def createTree(dataSet,labels): classList=[example[-1] for example in dataSet] #类别相同,停止划分 if classList.count(classList[-1])==len(classList): return classList[-1] #长度为1,返回出现次数最多的类别 if len(classList[0])==1: return majorityCnt(classList) #按照信息增益最高选取分类特征属性 bestFeat=chooseBestFeatureToSplit(dataSet)#返回分类的特征序号 bestFeatLable=labels[bestFeat] #该特征的label myTree={bestFeatLable:{}} #构建树的字典 del(labels[bestFeat]) #从labels的list中删除该label featValues=[example[bestFeat] for example in dataSet] uniqueVals=set(featValues) for value in uniqueVals: subLables=labels[:] #子集合 #构建数据的子集合,并进行递归 myTree[bestFeatLable][value]=createTree(splitDataSet(dataSet,bestFeat,value),subLables) return myTree #5.决策树用于分类 #输入三个变量(决策树,属性特征标签,测试的数据) def classify(inputTree,featLables,testVec): firstStr=list(inputTree.keys())[0] #获取树的第一个特征属性 # print(firstStr) secondDict=inputTree[firstStr] #树的分支,子集合Dict featIndex=featLables.index(firstStr) #获取决策树第一层在featLables中的位置 for key in secondDict.keys(): if testVec[featIndex]==key: if type(secondDict[key]).__name__=='dict': classLabel=classify(secondDict[key],featLables,testVec) else:classLabel=secondDict[key] return classLabel #6.决策树的存储 def storeTree(inputTree,filename): import pickle fw=open(filename,'wb') #pickle默认方式是二进制,需要制定'wb' pickle.dump(inputTree,fw) fw.close() #7.决策树的读取 def grabTree(filename): import pickle fr=open(filename,'rb')#需要制定'rb',以byte形式读取 return pickle.load(fr) #8.决策树的存储(json版) # def storeTree(inputTree,filename): # import json # fw=open(filename,'w') #json默认是转换成字符串类型 # json.dump(inputTree,fw) # fw.close() #9.决策树的读取(json版) # def grabTree(filename): # import json # fr=open(filename,'r') # return json.load(fr)
3.对上述的决策树进行相应的测试
#1.测试构建的的数据 import trees myDat,labels = trees.createDataSet() # print(myDat)#[[1, 1, 'yes'], [1, 1, 'yes'], [1, 0, 'no'], [0, 1, 'no'], [0, 1, 'no']] # print(labels)#['no surfacing', 'flippers'] #2.测试香农滴函数 a=trees.calcShannonEnt(myDat) # print(a)#0.9709505944546686 #3.测试按照特征划分数据集的函数 from imp import reload b=reload(trees) # print(b)#<module 'trees' from 'D:\\project\\test\\trees.py'> c=trees.splitDataSet(myDat,0,0) # print(c)#[[1, 'no'], [1, 'no']] d=trees.splitDataSet(myDat,0,1) # print(d)#[[1, 'yes'], [1, 'yes'], [0, 'no']] #4.测试chooseBestFeatureToSplit函数 e=trees.chooseBestFeatureToSplit(myDat) # print(e) #5.#决策树构造函数测试 myTree=trees.createTree(myDat,labels) # print(myTree)#{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}} #6.对决策树分类函数进行测试 myDat,labels=trees.createDataSet() # print(trees.classify(myTree,labels,[1,0]))#no # print(trees.classify(myTree,labels,[1,1]))#yes #7.对决策树的存储和读取函数进行测试 trees.storeTree(myTree,'classifierStorage.txt') g=trees.grabTree('classifierStorage.txt') # print(g)#{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号