数据结构之---红黑树

红黑树在二叉树和平衡二叉树的基础上做了点改进。

红黑树有5个特性：

1）每个节点非红即黑

2）根节点为黑色的

3）叶子节点为黑色的空节点

4）红色节点的子节点必为黑色

5）任意节点到叶子节点过程中都有相同数量的黑色节点

也就是说之后无论红黑树怎样变换操作，插入或者删除都需要维持在以上五个特性内。

那么其实只要将插入和删除的场景一一列举出，将节点套入其中即可。

 

为了维持以上五个特性红黑树的一般操作：变色和旋转

变色即红变黑，黑变红，旋转分为左旋和右旋（下图方便理解旋转）

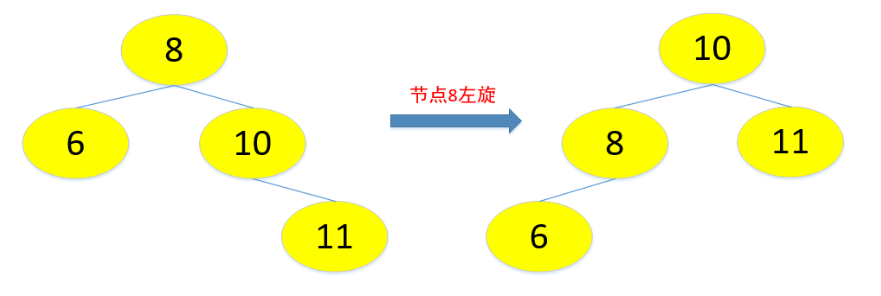
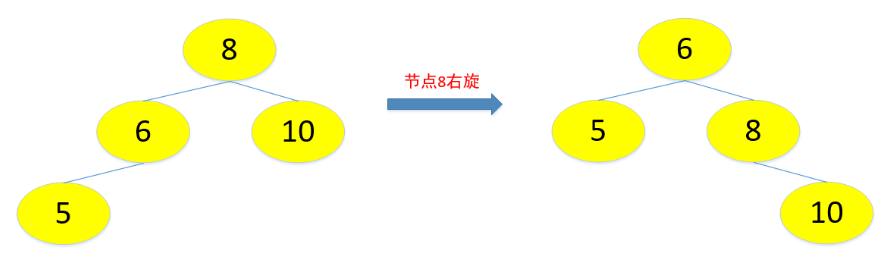
接下来看插入和删除的场景：

插入简单自行百度。

删除：

删除的情况大致分四种：

1）删除的节点左右子树都非空。

2）删除的节点左子树为空，右子树非空。

3）删除的节点右子树为空，左子树非空。

4）删除的左右子树都为空。

先看第一种情况：左右子树非空，这种情况的做法是找前继节点或者后继节点。以后继节点为例，

后继节点为删除节点右子树中最小的节点。

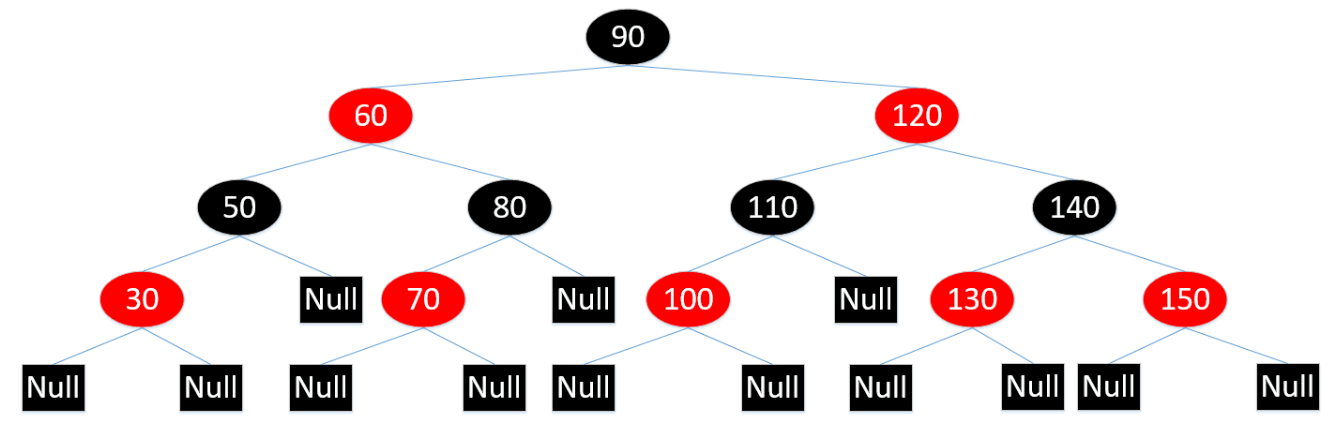
如上图以删除节点60为例子，它的后继节点为70。可以看到后继节点有个特点，后继节点的左子树肯定为空，因为不为空的话它就不是后继节点，而右子树不确定。

也就是将130的值替换到60，并继承60的所有属性（颜色和关系）之后将原70 的实体删掉。（这一点不理解的咱们可以通过图来分析，如上图60为删除的节点，删除后对80进行右旋，70就顶上了原60的位置，即删除的是70的壳）

综上可知，情况一可以间接的转换到情况二，三，四。

接下来看情况二三：只有一个子节点

1.1 如果删除的为红色节点且只有一个孩子，那根据特征4，其子节点为黑色。但是子节点为黑色有违背特征5。故这种情况不存在  X

1.2 删除的节点为黑色，那么唯一的子节点由特征5推出必为红色。 √ 

维持平衡处理：右子节点（35）替换到删除节点（30）的位置，并涂黑，删除右子节点

                              

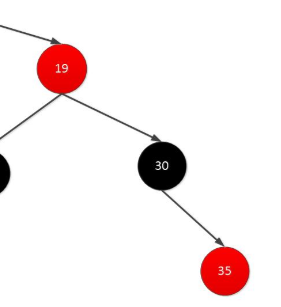
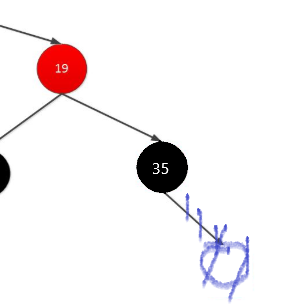
情况四：为叶子节点

2.1 首先删除的节点为红色，则可以直接删除，结束  √

2.2 删除的节点为黑色，则不可能通过涂色的方式弥补缺少的黑色，只能通过兄弟临近分支旋转来保持特征平衡

　　2.2.1 如果兄弟节点为黑色,那么它的子节点要么为空要么为红

　　　　1）若兄弟节点的两个子节点为空，且该节点父节点为红

　　　　　　为了保证左右两分支的黑色数量，将要删除的节点和它兄弟节点的父节点（红色节点）变为黑色，然后将兄弟节点变为红色 √

　　　　 

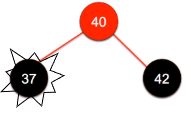
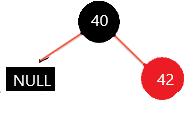
　　　　2）若兄弟节点的两个子节点为空，且该节点父节点为黑

　　　　　　此时删掉左子树后缺少一颗黑色，为维持平衡只能先将右子树涂红，但是涂红后他们俩的父节点本身为黑，

　　　　　　所以只能将它们的父节点作为删除的节点再次交给上一层处理，即回到2.2（变色的原则保证原始的黑色数量一致，即假如父红两子黑，则在不违反特性下可以变为父黑两子红）

　　　　

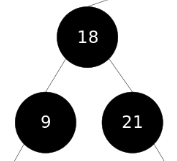
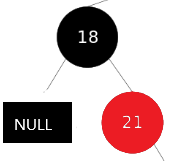
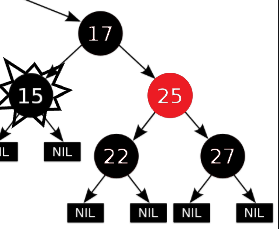
　　　　3）若兄弟节点的两个子节点为红（左子节点为红）

 

　　　　　　

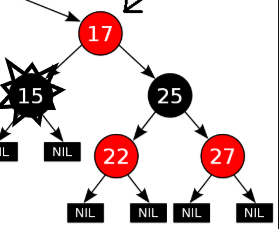
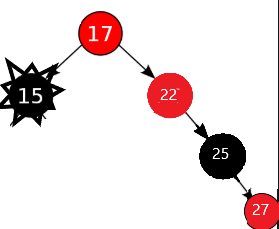
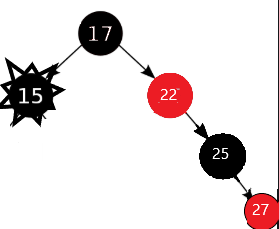
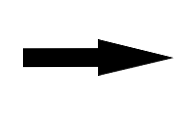
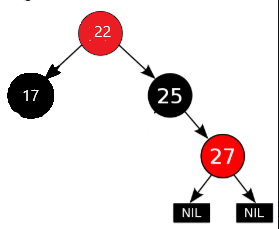
　　　　4）若兄弟节点的两个子节点为红（左子节点为空，灰色为不关心颜色）

　　　　

 

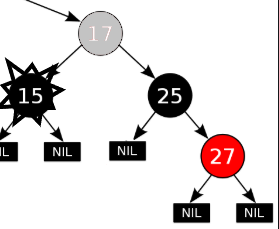
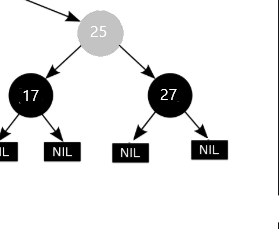
2.3 如果兄弟节点为红色，则兄弟节点的两个子节点有且为黑色，这种情况类似兄弟节点为黑的场景，需要将父节点作为删除的节点重新交给上一层处理