[Atcoder]ABC266题解
C - Convex Quadrilateral
计算几何
给定平面内四个点,要求判断它们组成的四边形是否是凸四边形
法一:
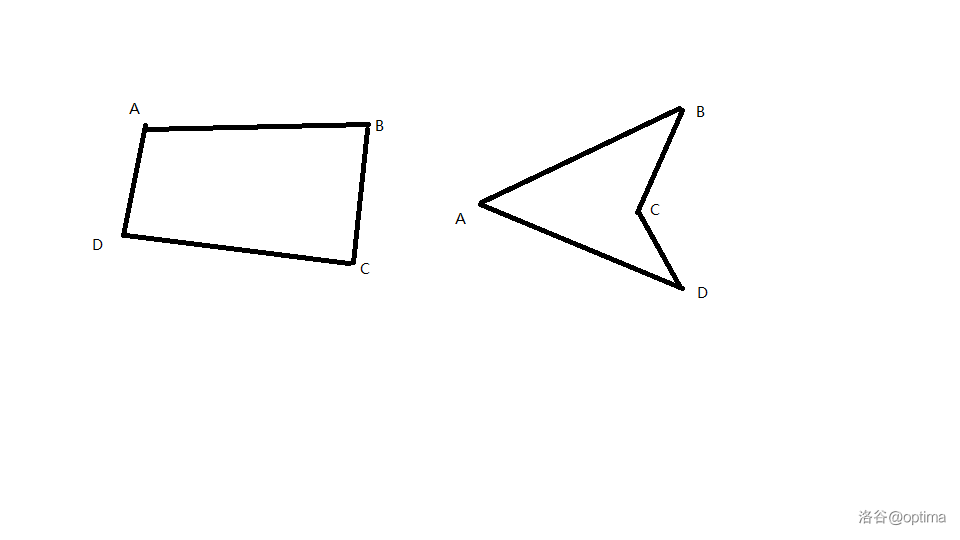
凸四边形的两条对角线将其分成两个三角形
分成的两个三角形面积相加等于四边形的面积
而显然这个结论对于凹四边形不成立
那么我们就可以利用这个结论进行解题
三角形面积用海伦公式求解,注意精度误差
补充几个求三角形面积的奇技淫巧

(鞋带定理(Shoelace formula)求2D多边形面积 - 简书 (jianshu.com))
#include <bits/stdc++.h>
#define ld long double
#define eps 1e-6
using namespace std;
int ax,ay,bx,by,cx,cy,dx,dy;
int sqr(int x)
{
return x*x;
}
ld Len(int x1,int yx,int x2,int y2)
{
return sqrt((ld)sqr(x1-x2)+(ld)sqr(yx-y2));
}
ld S(int x1,int x2,int yx,int y2,int z1,int z2)
{
ld a=Len(x1,x2,yx,y2),b=Len(x1,x2,z1,z2),c=Len(yx,y2,z1,z2);
ld p=(a+b+c)/2;
return sqrt(p*(p-a)*(p-b)*(p-c));
}
int main()
{
scanf("%d%d%d%d%d%d%d%d",&ax,&ay,&bx,&by,&cx,&cy,&dx,&dy);
if (fabs(S(ax,ay,bx,by,cx,cy)+S(ax,ay,cx,cy,dx,dy)-S(ax,ay,bx,by,dx,dy)-S(bx,by,cx,cy,dx,dy))>eps)
printf("No");
else printf("Yes");
return 0;
}
法二:向量求解
对于三点\(A(A_x,A_y),O(0,0),B(B_x,B_y)\),\(\angle AOB\)小于\(180^{\circ}\)当且仅当\(A_xB_y-A_yB_x>0\)(角度按逆时针记,如下图)
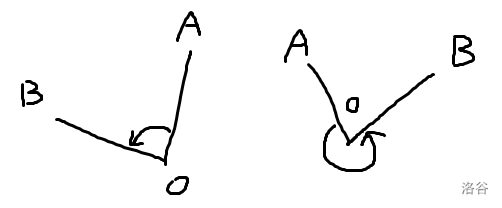
证明:
现有向量\(\vec{OA}\),\(\vec{OB}\),将\(\vec{OB}\)绕原点顺时针旋转90度得到\(\vec{OB^{'}}\)
1.若\(\angle AOB<180^{\circ}\),那么\(\angle AOB^{'} <90^{\circ}\)
\(\vec{OA}\cdot\vec{OB}=A_xB_y-A_yB_x=|\vec{OA}|\cdot|\vec{OB}|\cdot cos\angle AOB^{'}>0\)
所以\(A_xB_y-A_yB_x>0\)
2.若\(180^{\circ}<\angle AOB < 360^\circ\),则\(90^{\circ}<\angle AOB^{'} < 270^\circ\)
\(\vec{OA}\cdot\vec{OB}=A_xB_y-A_yB_x=|\vec{OA}|\cdot|\vec{OB}|\cdot cos\angle AOB^{'}<0\)
所以\(A_xB_y-A_yB_x<0\)
证毕.
又注意到对于一个凸四边形,以逆时针计的角必定要么全部小于\(180^{\circ}\),要么全部大于\(180^{\circ}\),那么我们就可判定凸四边形了.
#include <bits/stdc++.h>
using namespace std;
int a[7],b[7];
int tag;
int calcu(int x,int y,int z)
{
int ax=a[x]-a[y],ay=b[x]-b[y];
int bx=a[z]-a[y],by=b[z]-b[y];
return ax*by-ay*bx;
}
int main()
{
for (int i=1;i<=4;i++)
scanf("%d %d",&a[i],&b[i]);
a[5]=a[1],b[5]=b[1];
a[6]=a[2],b[6]=b[2];
tag=calcu(1,2,3);
for (int i=3;i<=5;i++)
{
int tmp=calcu(i-1,i,i+1);
if (tmp*tag<=0)
{
printf("No");
//system("pause");
return 0;
}
}
printf("Yes");
//system("pause");
return 0;
}
D - Snuke Panic(1D)
动态规划
设\(f[i][j]\)表示i时刻时在j位置的最大值\((j\in[0,4] \ \&\&\ i,j\in\textbf Z)\)
直接转移即可
#include <bits/stdc++.h>
#define int long long
using namespace std;
int n,f[100010][5],lst,ans=-1;
struct node
{
int t,a,x;
}q[100010];
struct node2
{
int a,x;
}w[100010];
signed main()
{
scanf("%lld",&n);
for (int i=1;i<=n;i++)
{
scanf("%lld %lld %lld",&q[i].t,&q[i].x,&q[i].a);
w[q[i].t].a=q[i].a;
w[q[i].t].x=q[i].x;
lst=max(lst,q[i].t);
}
memset(f,-1,sizeof(f));
f[0][0]=0;
for (int i=1;i<=lst;i++)
{
for (int j=0;j<=4;j++)
{
if (j==0) f[i][j]=max(f[i-1][j],f[i-1][j+1]);
else if(j==4) f[i][j]=max(f[i-1][j-1],f[i-1][j]);
else f[i][j]=max(f[i-1][j-1],max(f[i-1][j],f[i-1][j+1]));
}
if (f[i][w[i].x]!=-1) f[i][w[i].x]+=w[i].a;
}
for (int i=0;i<=4;i++)
ans=max(ans,f[lst][i]);
printf("%lld",ans);
//system("pause");
return 0;
}
E - Throwing the Die
动态规划
设\(f[i]\)表示还剩\(i\)步时的期望最大得分.
\(f[i]=\frac{1}{6}max(1,f[i-1])+\frac{1}{6}max(2,f[i-1])+\frac{1}{6}max(3,f[i-1])+\frac{1}{6}max(4,f[i-1])+\frac{1}{6}max(5,f[i-1])+\frac{1}{6}max(6,f[i-1]).\)
#include <bits/stdc++.h>
using namespace std;
int n;
double f[110],qua;
int main()
{
scanf("%d",&n);
qua=1.0/6.0;
for (int i=1;i<=n;i++)
for (int j=1;j<=6;j++)
f[i]+=qua*max((double)j,f[i-1]);
printf("%.8lf",f[n]);
//system("pause");
return 0;
}
F - Well-defined Path Queries on a Namori
注意到给定的图是\(n\)个点\(n\)条边,那么这就是一个基环树.
只存在一个环和若干棵根节点在环上的树.
那么我们只需要\(DFS\)找出这个环以及环上的节点.
若在同一颗树上,则路径唯一.
#include <bits/stdc++.h>
#define N 200010
using namespace std;
int n,inn[N],tag[N],fa[N];
int a,b,T;
bool v[N];
vector <int> G[N];
priority_queue < pair<int,int> > q;
void dfs(int x,int val)
{
for (int i=0;i<G[x].size();i++)
{
if ((!v[G[x][i]]) || (fa[x]==G[x][i])) continue;
tag[G[x][i]]=val;
fa[G[x][i]]=x;
dfs(G[x][i],val);
}
}
int main()
{
scanf("%d",&n);
for (int i=1;i<=n;i++)
{
scanf("%d %d",&a,&b);
inn[a]++;
inn[b]++;
G[a].push_back(b);
G[b].push_back(a);
}
for (int i=1;i<=n;i++)
q.push({-inn[i],i});
while ((!q.empty()) && (q.top().first==-1))
{
int x=q.top().second;
q.pop();
if (v[x]==-1) continue;
v[x]=1;
for (int i=0;i<G[x].size();i++)
{
if (v[G[x][i]]) continue;
inn[G[x][i]]--;
q.push({-inn[G[x][i]],G[x][i]});
}
}
for (int i=1;i<=n;i++)
{
if (v[i]) continue;
tag[i]=i;
dfs(i,i);
/*cout << endl;
for (int i=1;i<=n;i++)
printf("%d\n",tag[i]);*/
}
/*for (int i=1;i<=n;i++)
if (!v[i]) printf("%d\n",i);
cout << endl;
for (int i=1;i<=n;i++)
printf("%d\n",tag[i]);*/
scanf("%d",&T);
for (int i=1;i<=T;i++)
{
scanf("%d %d",&a,&b);
if ((v[a]==0) && (tag[b]==a)) printf("Yes\n");
else if ((v[b]==0) && (tag[a]==b)) printf("Yes\n");
else if (tag[a]==tag[b]) printf("Yes\n");
else printf("No\n");
}
//system("pause");
return 0;
}
G - Yet Another RGB Sequence
组合数学
我们将原问题看作r-k个'R',g-k个'G',b个'B',k个'K'组合,要求不能出现'RG',求有多少种排列.
#include <bits/stdc++.h>
#define P 998244353
#define ll long long
using namespace std;
int r,g,b,k;
int fac[2000020];
ll ans=1ll;
int qpow(int x,int y)
{
int ans=1;
while (y)
{
if (y&1) ans=(1ll*ans*x)%P;
x=(1ll*x*x)%P;
y>>=1;
}
return ans;
}
int main()
{
scanf("%d %d %d %d",&r,&g,&b,&k);
r-=k;g-=k;
fac[0]=1;
for (int i=1;i<=2000010;i++)
fac[i]=(1ll*fac[i-1]*i)%P;
for (int i=1;i<=k+g+b;i++)
ans=(1ll*ans*i)%P;
ans=ans*qpow(fac[k],P-2)%P*qpow(fac[g],P-2)%P*qpow(fac[b],P-2)%P*fac[k+b+r]%P*qpow(fac[r],P-2)*qpow(fac[k+b],P-2)%P;
printf("%lld",ans);
//system("pause");
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号