逆向思维

当我们遇到一道算法题，有时候从正面解决问题很困难，或者根本不能解决问题，那么这时候既可以从反面来思考；

只是通过文字说明是不行的，来看两道例题，让我们锻炼一下自己的思维；

T1：滑雪场设计

题目

​

​

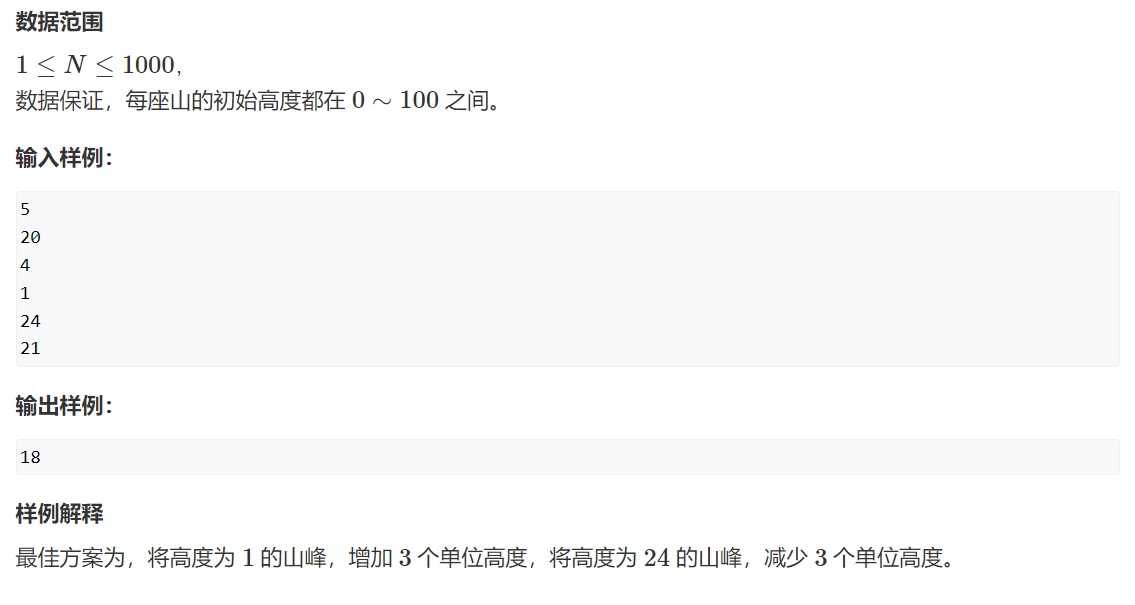
思路

开始准备用贪心来做，后来发现山峰的高度变换后，可能导致一系列问题，比如最高峰和最低峰变成了其他山峰，因为有后效性，所以无法直接使用贪心。

换一种思路：

修改后，任意两个山峰之间距离不大于17;也就是最大值与最小值的差为17;

每座山的初始高度都在 0∼100 之间，如果修改后最低的山峰为0的话，最高的山峰就是17，如果修改后最低的山峰为50的话，最高的山峰就是57；

修改后，最低的山峰的范围为0~83，对应最高的山峰为17~100；

因此我们只需要枚举这83种情况，比最低峰小的话就加上，比最高峰大的话就减去；

代码

#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>

using namespace std;
const int N = 1010;
int n;
int h[N];
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++) cin>>h[i]; //输入
    int ans=1e8; 
    //枚举83种情况，比最低峰小的话就加上，比最高峰大的话就减去；
    for(int i=0;i<=83;i++) //枚举83种情况
    {
        int res=0;
        for(int j=1;j<=n;j++)
        {
            if(h[j]<i) res+=pow(i-h[j],2); //小于最低峰
            else if(h[j]>i+17) res+=pow(h[j]-i-17,2); //大于最高峰
        }
        ans=min(res,ans); //找到最小的差值
    }
    cout<<ans;
    return 0;
}

T2：里程表

题目

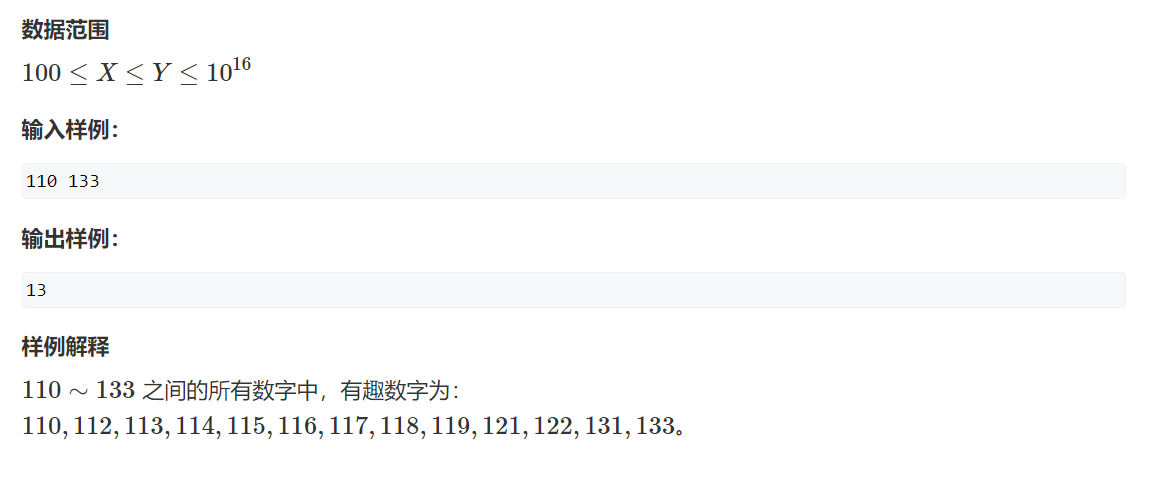
思路

一看这道题数据范围大的快上天了，哪怕把所有的数字循环一次都会TLE。

并不难，就是在于逆向思维。

我们就可以换一个角度想，因为“有趣的数”并不多，所以我们可以先枚举出每一个“有趣的数”，最后判断区间(x,y)(x,y)之间有几个“有趣的数”即可。

枚举的层次：

数字长度->构造一个各位全部相同的数字->新的数字k，判重并改字符->统计答案

代码

//预处理出来所有的有趣的数字
#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;
long long x,y,ans; //不开long long见祖宗
int main()
{
    cin>>x>>y;
    for(int i=3;i<=17;i++) //i表示数字的长度
    {
        for(int j=0;j<=9;j++) //相同的数字
        {
            //构造一个字符串strstr，长度为i，并且把每一位都赋值为j这个数
            //但是在这里要转化为字符形式
            string str(i, '0' +j);
            for(int k=0;k<=9;k++) //不同的数字
            {
                if(k==j) continue; //判重
                for(int p=0;p<i;p++)
                {
                    str[p]='0'+k; //有趣的数字
                    //再转换成number
                    long long t=0;
                    for(int q=0;q<i;q++) t=t*10+(str[q]-'0');
                    if(str[0]! ='0'&&t>=x&&t<=y) ans++;
                    str[p]='0'+j; //还原现场,进行下一次循环
                }
            }
        }
    }
    cout<<ans;
    return 0;
}