DP 专题

DP 专题

Make It Ascending

操作可以看成每次吧一些数提出来求和在选一个这次提出来的数的位置放入，不妨钦定每次都只能向上一次的后面放。

容易发现对后续的影响只在于前缀最大值和前缀位置，设 \(dp_{i, j, s, k}\) 表示当前是第 \(i\) 次选，上一次的位置是 \(j\)，没选的状态为 \(s\), 和为 \(k\) 是否可行，简单键值互换变成 \(dp_{i, j, s}\) 表示最大的 \(k\)。

直接转移是 \(n ^ 2 3 ^ n\) 的，但是由于若 \(i, j, s\) 不存在就可以不转移所以严格跑不满，能过。

考虑优化，先枚举 \(s, t \subseteq s\) 发现 \(i, j, dp_{i, j, s}\) 本质是一个二维偏序，于是我们排掉 \(dp_{i, j, s}\)，暴力数组维护下标为 \(i\) 的 \(min\{j\}\)，瓶颈在排序，为 \(\mathcal O(3 ^ n \log 3 ^ n) = \mathcal O(n3^n)\)，实测并不快就是了。

Turtle

首先考虑到若上下的数确定了，则最优一定是将上面降序下面升序，所以我们其实就是将它们上下分组。

然后考虑继续挖掘上升下降的性质，发现最优点一定是在第一个或最后一个格子处向下，这个考虑反证或归纳也不太难。

先去掉必然被算的左上右下角，问题就是将数组分成上下个数相等的两组，最小化其中较大的和，这显然是个 \(n ^ 2 V\) 的背包。

如果暴力枚举左上右下角则复杂度不太好接受，但是容易发现左上右下角填最小和次小一定不劣，于是就做完了。

Chess Rush

除了象和王其他都不难。

象其实也还好，考虑最优解一定是除了最后每次都碰边，也可以理解为每次碰边最后在微调。

考虑微调，发现每往里早折一下都会使落纵坐标偏移 \(2\)，且偏移方向之和最后一次折的方向有关，是固定的，落点纵坐标和目标纵坐标的差是固定的，于是就是一个插板。

王如果没有边界就是简单问题，GF 求 \((x + 1 + \frac 1x) ^ k\) 即可。

考虑边界，发现我们的问题就是想让边界处的 dp 动态置 \(0\)，于是我们和它对称做一个反着的 dp 并在边界上相交，如下图（图片来自 luogu，侵删）：

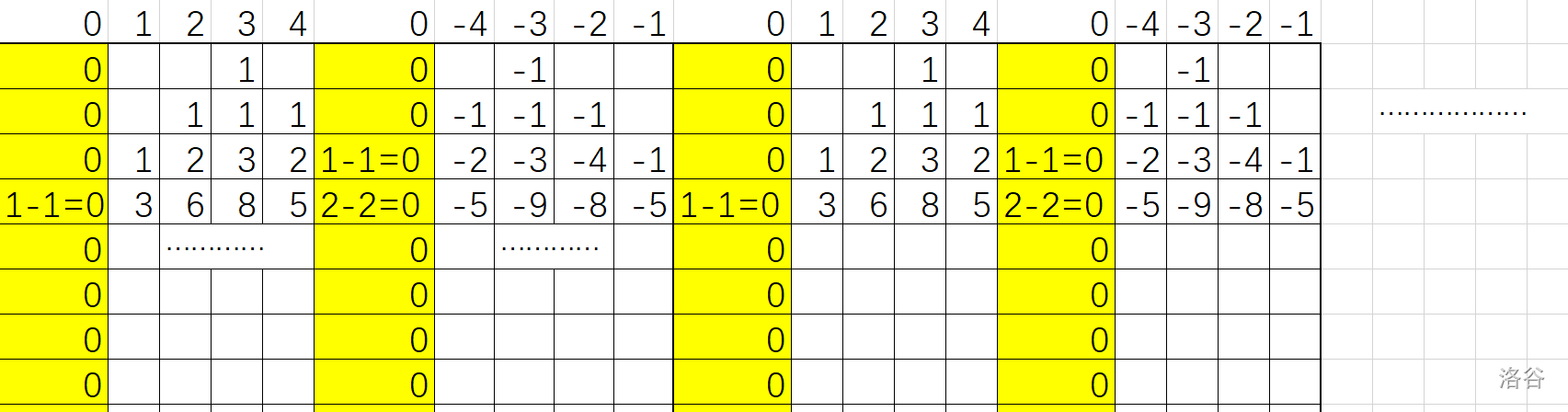
但是我们不可能维护一个无限长的序列，容易发现其 \(2c + 2\) 行是循环的，于是我们施以循环卷积即可，形象点说像是圆柱的侧面正反 dp 各一半。也可以说是反射容斥。

Puzzle Lover

考虑路径一定是（图片来自 luogu，侵删）：

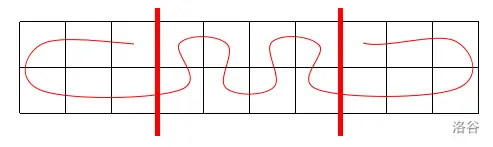
将前后段拆开，中间的折叠进行 dp，设 \(dp_{i, j, k}\) 表示第 \(i\) 行第 \(j\) 列是否能匹配前 \(k\) 个，转移比较显。

注意到只有两行，所以复杂度是 \(\mathcal O(n ^ 2)\) 的。

难度全在实现上了。

Finding satisfactory solutions

考虑正着怎么做，设 \(A \to B\) 表示 \(A\) 最喜欢 \(B\)，若 \(A \to B \to C \dots \to A\) 即连成环，则一定不会和环外的交换，我们可以删掉环递归子问题。

想到建图，形式化来说，对于给定的 \(\{a\}\)，我们让 \(i \to a_i\) 连黑边，\(i\) 和若干其它点连白边，使环中不存在白边。

考虑黑边一定连成若干环，我们将其缩点，就变成了模板 DAG 计数，不会的看我鲜花。

直接整是 \(3 ^ n\) 枚举子集的，但是我们发现其只有转移算贡献时用到了具体的子集，但是也只是用到了总点数也就是环的大小。

所以我们压缩状态成大小为 \(x\) 的环有几个，可以证明状态数十分的少。

Number of Binominal Coefficients

结论题。

考虑库默尔定理，即 \(\dbinom{a + b}{a}\) 中素数 \(p\) 的次数等于 \(n + m\) 在 \(p\) 进制下的进位次数。

证明考虑 \(\nu(p) = \sum\limits_{i = 1} (\lfloor\frac{a + b}{p ^ i}\rfloor - \lfloor\frac{a}{p ^ i}\rfloor - \lfloor\frac{b}{p ^ i}\rfloor)\)，然后每进位一次就会有 \(1\) 的贡献。

然后就是一个非常不好写的数位 dp，设 \(dp_{i, j, 0/1, 0/1}\) 表示当前是第 \(i\) 位，进位 \(j\) 次，是否卡上界，是否接受下位进位。

[agc034_e]Complete Compress

简单题，咋写都行。

设 \(dp_{i, j} = 0/1\) 表示树上第 \(i\) 个点，还可以在子树内往上走 \(j\) 步是否可行，换个根即可 \(n ^ 2\)。

或者发现性质，\(j\) 等于 \(1\) 一定是一段公差为 \(2\) 的等差连续区间，直接记录左右端点即可，换根的话是 \(\mathcal{O}(n)\)，不换也无所谓。

[agc020_e]Encoding Subsets

堂食题，难点在于敢写。

考虑若只算原串怎么写，设 \(f_{l, r}\) 表示 \([l, r]\) 的方案数，\(g_{l, r}\) 表示 \([l, r]\) 缩成一个括号或一个数的方案数，\(f\) 转移枚举前缀缩成一个括号，\(g\) 枚举循环节长度 \(len\)。

考虑子串就是暴力，设 \(f_S\) 表示 \(S\) 串压缩的方案数，\(g_S\) 表示 \(S\) 缩成一个括号或一个数的方案，\(f\) 转移依然枚举前缀，\(g\) 转移枚举长度枚举循环节交即可。

复杂度分析我只会到 \(\mathcal{O}(n^5\log n + n ^ 22 ^n)\) 常熟巨小，敢写敢过。

[agc036_d]Negative Cycle

水了标签就会了题。

考虑差分约束。

将原图看成一个差分约束图，没有负环等价于存在一组合法解。因为最开始的链没法删，所以一定有 \(a_i \ge a_{i + 1}\)。

不妨考虑差分数组 \(q_i\)，考虑一条前向边等价与区间和 \(\le 1\)，后向边等价于和 \(\ge 1\)。

所以确定了 \(q\)，一个区间和 \(= 0\) 则删掉后向边，\(\ge 2\) 删除前向边。

容易发现 \(q\) 只有 \(0/1\) 两种取值，并且只与前一个一有关，记录一下 \(dp\) 即可。

[agc028_d]Chords

trick 挺牛的。

发现统计最后的状态是难的，考虑划分一个状态统计起出现次数和。

破成链是简单的，考虑用一个连通块中最左的点 \(l\) 和最右的点 \(r\) 来表示一类连通块 \([l, r]\)。两类连通块一定不是包含就是相离。

然后就暴力 dp，设 \(dp_{l, r}\) 表示 \([l, r]\) 为一个联通块的方案数，转移容斥即可。

设 \(g(x)\) 表示 \(x\) 个点的环的连边方案数，对于 \(x\) 为偶数时值为 \(\sum\limits_{i = 1}^{\frac{x}{2}} (i * 2 - 1)\)，奇数时为 \(0\)，\(c_{l, r}\) 表示 \([l, r]\) 中未连边的点的个数。

给个方程：

\[dp_{l, r} = g(c_{l, r}) - \sum_{i = l} ^ {r - 1} dp_{l, i} * g(c_{i + 1, r}) \]

[agc022_f]Checkers

抽象题，我会 \(n ^ 5\)。

首先题目相当于是将 \(a, b\) 合并成新数 \(b * 2 - a\) 放入集合中，为最后剩下的数的种类数。

想到建图，可以将 \(b \to a\) 或 \(a \to x, b \to x\) 即建一个虚点，分别对应两种做法，第一个可以看 wang5 的，我只会第二个。

我们钦定 \(\times 2\) 作为左子树，\(\times (-1)\) 作为右子树，容易发现对于左子树，其多走一步就不一样（\(2 ^ n < X\)），但对于右子树只和其步数奇偶有关。

所以按左子树分层，每层的方案数不同，同层之间记录 \(-1, 1\) 的个数，转移即可。

具体的，设 \(dp_{i, j, a, b}\) 表示第 \(i\) 层，填了 \(j\) 个叶子（题目相当于是填恰好 \(n\) 个叶子），\(-1\) 有 \(a\) 个，\(1\) 有 \(b\) 个，暴力枚举本层扩展多少个 \(-1 , 1\) 即可转移，发现最后答案和转移均没用到 \(i\) 可以去掉，复杂度就是 \(\mathcal{O}(n ^ 5)\) 了，常熟比较小。

【UR #20】跳蚤电话

两种想法，一是发现最开始一定是 \(1 \to u\) 连边，然后 \(u\) 子树内就不可能向 \(u\) 的祖先连边，然后就划分子问题了。

或者是倒着做相当于是每次删一个 \(1/2\) 度点，设 \(dp_u\) 表示钦定 \(u\) 不删其子树的方案数，枚举最后一个删的是 \(v\)，则 \(v\) 子树内和 \(v\) 子树外依然无关。

这样暴力 \(dp\) 是 \(n ^ 2\) 的，发现对于 \(u\) 和其儿子 \(v\)，其贡献是差不多的，所以我们每次只枚举孙子，加上其儿子即可达到 \(\mathcal{O}(n)\)。

精细的把转移式子拆开即可得到一个不用 dp 的式子（这里转成概率做的，最后乘上 \((n - 1)!\) 即可）：\(f_i=\prod\limits_{j \in subtree_i}\frac{1}{siz_j}(1+\sum\limits_{k\in son_j}\frac{siz_k}{siz_j-siz_k})\)，暴力做即可。

【UR #12】密码锁

主旋律狂拿场上最高分 \(49 pts\) 还在发力！

发现图是个竞赛图，所以缩点以后是链状结构，后面的的点连向前面的点，链长即是答案。

链长等于链非空前缀个数，统计非空前缀个数即可。发现一个点集是一个合法的前缀当且仅当所有属于它的点和不属于它的点之间的边全部指向外边，暴力枚举点集即可 \(42 pts\)。

考虑最后 \(m\) 实际上非常小，考虑实现一个指数上只和 \(m\) 有关的做法，若 \(m = 0\) 则有 \(x\) 个点的集合概率是 \(\frac 1{2^{x(n - x)}}\)，若一个特殊边，我们乘上系数 \(2P\) 即可。我们枚举有那些特殊边产生了限制，然后给图黑白染色，产生限制的边左右点颜色不同，不产生限制的相同，无解则不合法。这样每次必然取黑点或白点作为前缀的一部分，对所有连通块跑个背包即可。

可以退背包实现 \(n2^m\)，但是有更简单的做法，我们对每个连通块分开做，每次直接加入到一个背包中，最后做背包合并即可，相当于多重背包，不过把状态合并了一下。复杂度为 \(\mathcal{O}(n2^m + n^2)\)。

【UR #17】滑稽树上滑稽果

简单题。

就是首先你读对题。

发现最优解一定是一条链，具体就是考虑若有多个点连一个点，将多个点排成链一定不劣。

所以这个特殊性质就是在万元神。

题解：

设 \(dp_{S, x}\) 表示当前还剩 \(S\)，\(\mathrm{And}\) 为 \(x\) 的最小值，转移枚举这次用那个即可。

发现对于 \(a_i\) 重复使用其并不会让结果变优，于是设 \(dp_{i, x}\) 表示长度为 \(i\) 的链，\(\mathrm{And}\) 为 \(x\) 的最小值，这样复杂度是 \(\mathcal{O}(n ^ 2a)\) 的。

发现 \(i\) 无意义，将一定保留到最后的单算即可把 \(i\) 去掉。发现若用 \(a_i \And x = x\) 的 \(x\) 更新即把 \(a_i\) 的作用缩小也没问题，因此直接枚举子集高位前缀和判断是否合法即可。

复杂度 \(\mathcal{O}(3 ^ {log_2 a}) = \mathcal{O}(a^{log_23})\)

【UNR #2】梦中的题面

也是简单题。

先考虑 \(c = 1\)。

想到数位 dp，将每位拆开，相当于是每位可以填 \(0 \sim b - 1\)，从低位向高位 dp，设 \(dp_{i, j}\) 表示填到第 \(i\) 位，\(\sum x_i - n\) 向上一位的进位或借位 \(j\) 次（正为进位，负为借位），转移预处理出 \(pr_{c, s}\) 表示 \(c\) 个 \(0 \sim b - 1\) 个数和为 \(s\) 的方案数即可轻松转移，复杂度是 \(\mathcal{O}(m^3 b)\)。

考虑 \(c = 0\)，则相当于是钦定一些数所有位全填 \(0\)，最高位 \(+1\) 位填 \(1\)。在枚举 \(i\) 的时候判断 \(x_i\) 是否填 \(b\) 就相当于是 \(x_i\) 所有位填 \(0\)，这样每次可以填的数的个数是不确定的，加一维表示当前钦定全填 \(0\) 的个数即可。

复杂度 \(\mathcal{O}(m^4 b)\)。

完结撒花！！！