探索性思维——How to Solve It

我觉得这篇文章和什么都能扯上点关系，比如编程。

很多人已经讨论过数学与编程的关系了，这里不想过多探讨，只是简单提一下：有些人把数学贬低地一文不值，认为做一般的应用软件用不到数学；而有些人则把数学拔高到一个很高的位置，认为一些比较上层的领域像机器学习，包括其父、子类人工智能和深度学习都需要用到些相对晦涩的数学知识。我的看法是：尽自己的能力学习更多的数学知识总是没有坏处的。当然，辨证的来看，过度学习偏废了机器本身也就不说什么了（仁者仁智者智吧，王垠也写过一篇文章，我想附在这里：数学与编程，希望勿喷，这不是本文的主题：-），还有，我还不懂机器学习。

另外，由于文章已经很长了，还有很多在不同地方接触的很有意思的问题躺在了笔记本上没有写出来，后面可能挑选一些作为"怎样解题"表的实战部分的补充发表另外一篇文章（可能会延期一个月左右，毕竟快毕业了吗，毕业论文什么的大家都懂）；也有可能对一些相关的章节做一些必要的扩充。

此外，这些处理问题的方法是具有普适性的，我觉得甚至能上升到方法论（人们认识世界的根本方法，用什么样的方式、方法来观察事物和处理问题）的角度来探讨，并不局限于数学。而且其中有一部分是属于元知识，是一种关于思考的思考（比如回顾解题过程，就是一种思考思考过程的过程）。

行文之前，先祭上Polya 的"怎样解题"表：

• 第一:弄清问题（你必须弄清问题）
  • 未知数是什么？已知数据是什么？条件是什么？满足条件是否可能？要确定未知数，条件是否充分？或者它是否不充分？或者是多余的？或者是矛盾的？
  • 画张图。引入适当的符号。
  • 把条件的各个部分分开。你能否把它们写下来？
• 第二:拟定计划（找出已知数与未知数之间的联系。如果找不出直接的联系，你可能不得不考虑辅助问题。你应该最终得出一个求解的计划）
• 你以前见过它吗？你是否见过相同的问题而形式稍有不同？
• 你是否知道与此有关的问题？你是否知道一个可能用得上的定理？
• 看着未知数！试想出一个具有相同未知数或相似未知数的熟悉的问题。
• 这里有一个与你现在的问题有关，且早已解决的问题。你能不能利用它？你能利用它的结果吗？你能利用它的方法吗？为了能利用它，你是否应该引入某些辅助元素？
• 你能不能重新叙述这个问题？你能不能用不同的方式重新叙述它？
• 回到定义去。
• 如果你不能解决所提出的问题，可先解决一个与此有关的问题。你能不能想出一个更容易着手的有关问题？一个更普遍的问题？一个更特殊的问题？一个类比的问题？你能否解决这个问题的一部分？仅仅保持条件的一部分而舍去其余部分，这样对于未知数能确定到什么程度？它会怎样变化？你能不能从已知数据导出某些有用的东西？你能不能想出适于确定未知数的其它数据？如果需要的话，你能不能改变未知或数据，或者二者都改变，以使新未知数和新数据彼此更接近？
• 你是否利用了所有的已知数据？你是否利用了整个条件？你是否考虑了包含在问题中的所有必要的概念？
• 第三:实现计划（实现你的计划）
  • 实现你的求解计划，检验每一步骤。
  • 你能否清楚地看出这一步骤是正确的？你能否证明这一步骤是正确的？
• 第四:回顾（验算所得到的解）
  • 你能否检验这个论证？你能否用别的方法导出这个结果？你能不能一下子看出它来？
  • 你能不能把这结果或方法用于其他的问题？

---

中学时代，可能许多同学都曾一度被这些问题困扰：是的，这个解答好像还行，它看起来是正确的，但不借助外力，单凭我自己怎样才能想出这个答案呢？是的，这个实验好像还行，它看起来是个事实，但别人是怎样发现这个事实的呢？而且我自己怎样才能想出或发现它们呢？

作为一个著名的数学家兼数学教育家，G.Polya 认为学生除了掌握逻辑分析方法之外，还必须掌握探索性思维能力。研读波利亚的系列书籍，在不知不觉中就会发现自己寻找事物内在联系，追求事物本源的能力产生了一次巨大的飞跃。

其实，上述表中的方法，我们在中学时代或多或少不经意间使用过其中的一部分（比如检验解，变换求解方式，引入辅助元素，特殊化等等），但是恐怕对这些问题理解的深度很难有Polya 那样深刻、犀利；还有，正是因为这些方法具有普适性，因此可能会看起来太简单了些，但是大道至简，很多时候，简单比复杂难得多；而且不去实践，自己感悟总结的话，是不会真正体会到这些方法的用处的。

大脑预热:几个有启发性的小问题

• 一个作图题：在任意给定的三角形中做一正方形。使得正方形的两个顶点在三角形的底边上，另外两个顶点分别在三角形的两边上，给出你的作图方案。

这个问题容易解决吗？如果不容易的话，你是否会考虑弱化条件？看起来三个顶点都在三角形边线上的正方形，是容易画出来的，但是这样的话，正方形是不确定的，它会怎样变化呢？或者更直白的说，第四个角的位置是如果变化的？你是否应该画出更多的三个角在边线上的正方形，从而估测第四角的轨迹？（如果你能猜到它的轨迹是一条直线，再利用一些三角形相似的知识，我想你应该得到问题的答案了）

• 一个证明题：在不同平面上的两个角，其中一个角的每一边平行于另一角的对应边且方向相同。证明这两个角相等。

我们要证明的是立体几何中的一个基本定理，它看起来似乎是显然的。但是要知道，仅凭直觉上的臆测得到一个定理同忽略直觉上的感觉一样都是相当愚蠢的。回到问题本身上，你是否应当画张图，引入适当的符号？看着结论！可否尝试想起一个具有相同或相似结论的熟悉的定理？应该不难想出定理：如果两个三角形全等，则对应角相等。为了可能利用它，你是否应该引入两个三角形，通过证明它们全等来达到目的？看起来这两个三角形是容易寻找的，并且很容易满足两组边对应相等，那么如何证明第三组边想等呢？为了达到这个新的目标，你能尝试回忆起一个具有相同或相似结论的熟悉的定理吗？.....则两线相等？你是否应该引入一个四边形，并且证明它是平行四边形？但是怎么证明呢，你利用了全部前提了吗（一个角的每一边平行于另一角的对应边且方向相同）？我们得到了两组等长的平行线，这是不是一个很有趣的图形呢？如果你能通过这两个平行四边形证明第三个四边形是平行四边形，我想你也应该得到该问题的答案了。

• 一个速率问题：水以速率r 流进锥形容器。容器具有正圆锥形状，底是水平的，顶点在下方，底的半径是a，高为b。当水深为y 时，求水平面上升的速率。

这个问题假定你知道最简单的微积分和变化率的概念（个人认为关于微积分方面的知识，可以阅读湖南科学技术出版社出版的《微积分的屠龙宝刀》，一本简单易懂，能读出快感的书:）。回到问题上，未知数是什么？水深为y 时，水面上升的速率。你能否重新叙述得更不同些？水深y 的变化率。好，什么是变化率（回到定义去）？函数的导数。现在y 是函数吗？你能否想象y 是变化的？是的，水深y 随着时间而增加。这样y 是时间t 的函数对不对？现在，请引入适当的数学符号，你将怎样写出y 的变化率？dy/dt。好，现在这就是你的未知数，你必须用a，b，r，y 来表示它。顺便提一下，数据中有一个水流进容器的速率r，它是什么？你能用别的术语来描述它吗？r 是容器中水的体积的变化率。很好，你能用适当的符号把它写成来吗？r = dV/dt。好，现在你必须用a，b，dV/dt，y 来表示dy/dt，你将怎么做？如果你现在还看不出dy/dt 与数据间的联系，那么你能看出其它数据间的联系吗？例如y 与V 是否彼此独立？不，当y 增加，V 一定也增加。好，既然有联系了，这联系是什么？哦，V 是椎体在水深y 时的体积，但是我现在还不知道底的半径，不过，倒是不妨把它设为x，这样，我得到了V = πx^2y/3。很好，那么关于x 我们又知道些什么？它是否与y 独立？不，当水深y 增加，自由表面的半径x 也增加。这么说，它们之间是有联系的，这联系是什么？当然是相似三角形，x:y = a:b。你看，又多了个联系，我想你不会愿意错过从它那儿得到一点好处。别忘了，你希望知道的是y 与V 之间的联系。嗯，现在我可以重写V，即V = πa^2y^3/(3b^2)。很好，这看起来很像是个踏脚点，难道不是吗？但别忘了你的目标，未知数是什么？噢，是dy/dt。好，现在你必须找出dy/dt，dV/dt 与其它数据量之间的联系，但这里有的却是y，V 和其他数据量间的联系。你该怎么办？当然是微分！dV/dt = πa^2y^2/b^2)dy/dt = r。没错，就是它，整理一下，我得到了dy/dt = rb^2/(πa^2y^2)。哈哈，很好，看起来也没有想象的那么难呢？你说是不是？

探索法小词典(核心)

类比

先抛出我们需要求解的问题：求均匀四面体的重心。

要知道，若不具备积分与物理知识，这问题将会是很困难的。在阿基米德和伽利略时代，它就是一个相当严肃的科学问题。因此，如果我们希望用尽可能少的预备知识来解决它，我们就应该寻求一个较为简单的类比问题（好吧，造个句子先-:如果说简单是真理的标志，那么类比就是通往真理的桥梁）。那么什么是类比呢？比方说长方形的边长和长方体的面形成一种同构关系，这就是一种类比。那么，对于当前的问题来说，在平面上对应问题很自然地就是：求一均匀三角形的重心。

现在，我们有了两个问题而不是一个问题。但两个问题比起一个问题来可能还更容易回答——假定这两个问题能巧妙地联系起来的话。为了求解这个问题，我们必须了解一些关于重心的知识。下列原理似乎是可信的而且提出它来也很自然：若一物质系统S 由几部分组成，每一部分的重心都位于同一平面上，则该平面也必包含此整个系统S 的重心。

对于三角形来说，这一原理给出我们所需的一切。它指出三角形的重心位于三角形的平面上。因此，我们可以把三角形看成由平行于三角形某边的许多小条条（无限窄的平行四边形）所组成。如下图，每一个小条条的重心显然是它的中心，而所有这些中心位于连线CM 上，M 为AB 边的中点。

不难看出，通过三角形中线CM 的任何平面包含有三角形中所有平行小条条的重心。根据刚才给出的原理，可以得出结论：整个三角形的重心就在这一中线上。同理，它也必须在其他两条中线上，所以它必须是所有三根中线的公共交点。为了完善这个求解过程，现在我用纯几何方法（与任何力学上的假设无关）来证明三根中线交于一点。下面是我手画的草图，介于篇幅原因，就不给详细的证明了。

简单提一下：左图利用归谬法，假设三条中线并不交于同一点，那么BO:OM = B0':O'M = 2:1。至于为什么是2:1，根据右图那个平行四边形可证。要是求知欲再强一点，下一步你可能会想要去证明三角形的中位线长度是底边长的一半，嗯，好主意，你继续吧，不过需要注意的一点是，最后你极有可能需要去看下欧几里得的大部头著作《几何原本》，还可能发现他的第五公设（平行线理论）在理论上存在的缺陷:-

在搞懂了三角形的类比问题之后，我们就有了一个可以照着办的模型，四面体的情况就相对简单了。在解决我们用作模型的类比问题中，我们设想三角形是由平行于其一边AB 的平行小条条组成。现在我们设想四面体ABCD 也由平行于其一棱AB 的小条条所组成。组成三角形的小条条的中点全部位于连接棱AB 的中点M 与对棱CD 的同一平面上，我么不妨将此平面MCD 称为四面体的中面。如下图所示：

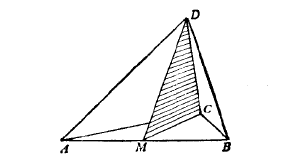
在三角形情况下，我们有象MC 那样的三根中线，其中每一根都必须包含三角形的重心。因此，这三根中线必须交于一点，这一点就是重心。类似地，在四面体情况下，我们有象MCD 那样的六个中面（连接一条棱中点与其对棱的平面），其中每个中面都必包含四面体的重心。因此，这六个中面必交于一点，这一点就是重心。这样，我们就解决了均与四面体的重心问题。为了完成这个求解过程，现在我们仍然只用纯几何知识（与任何力学上的考虑无关）来证明这六个中面通过同一点。当我们解决了三角形的重心问题以后，我们发现，为了完成求解过程，需要证明三角形的三条中线通过同一点。这个问题可类比上述问题，但显然要简单一些。

在解决四面体这一问题时，我们又可以利用较简单的三角形类比问题。事实上，我们考虑通过从D 点出发的三条棱DA，DB，DC 的三个中面，每一中面也通过对棱的中点。现在，这三个中面和△ABC 所在平面交于该三角形的三个中线。这三条中线交于一点（这里利用了前面较简单的类比问题的结果），而这点和D 点一样，也是三中面的公共点。连结这两个公共点的直线就是这三个中面的公共线。

我们证明了六个中面中通过顶点D 的三个中面有一条公共直线。对于通过顶点A/B/C 的三个中面，同样成立。接下来，我们从A 点出发得到的三中面中有一个和从D 点出发的三中面的公共面（设BC 的中点为N，那么这个公共面就是△ADN）。其上包含两组三中面的公共线，它们相交于一点。同样的道理，因为公共面的存在，我们可以得出从B 点出发的三中面的公共线分别与方才得到的两组公共线相交，假设它们彼此不相交于一点（这构成了一个平面）。那么，从C 点出发的公共线必然与方才的三组公共线分别相交，注意到这是不可能，因为从C 点出发的中线根本不存在，为什么呢？因为它的三个中面必然经过刚才提到的三组公共线（我们假设它们彼此不相交，从而构成了一个平面），而且这三个中面显然不是同一个平面，这种情况下，过方才三组公共线的三中面要形成一个公共交线是不可能的，这与我们先前得到的三中面有一个公共线是相矛盾的（这里利用了三角形那个较简单的类比问题的方法:归谬）。之所以得出错误的结果，是因为我们先前的假设就是错误的。于是问题得证。

这里关于三角形三中线共点、四面体六中面共点的证明过程作者都一笔带过了（可能也是限于篇幅原因吧:-）于是我自己就把它补充上了，当然证明方法多种多样、殊途同归，这些花式玩法自然有它的重要性（比如可以帮你深刻的理解一个定理，甚至是从直观上一眼就看出它来），但不是我们现在关注的焦点。当前我们需要做的是，仔细品味这个问题中类比给我们带来的好处（你能利用它的方法吗？你能利用它的结果吗？）。

如果我们知道均与棒的重心与其两端点的重心重合。均与三角形的重心与其三顶点的重心重合，为什么我们不应该设想均与四面体的重心与其四顶点的重心重合呢？

还有，均匀棒的重心按比例1:1 来划分其端点间的距离。均与三角形的重心按比例2:1 来划分任何顶点与其对边中点间的距离。为什么我们不应该猜测均与四面体的重心是按比例3:1 来划分任何顶点与其对面的重心间的距离呢？

辅助元素

一般说来，当我们想到一个早已解决的有关问题后，我们必须经常问：为了可能利用它，我们是否应该引入某个辅助元素？力图利用已知结果和回到定义去以及仅仅感觉到加上这样那样的元素用那种方式看问题是个"好念头"都可以成为我们引入辅助元素的很好的理由。

为了透彻的理解这一点，仍然是抛出一个相关的问题：已知三角形一角和由此角顶点向对边所作的高和三角形的周长，做这个三角形。

我们引入适当的符号，令已知角为α，从角α 的顶点A 向对边所作的高位h，已知周长为P。作图如下：

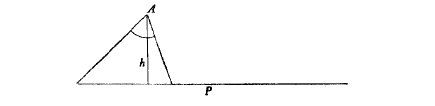
我们把三角形的三条未知边设为：a，b，c。于是有P = a + b + c。这里，边b 与边c 的作用是相同的，是可交换的，我们的问题关于b 和c 是对称的。但是在上图中，我们却看不到这一点，它破坏了问题对b 和c 的自然对称性。或许我们应该这样放置P，使得它和b 和c 的关系是对称的。

上述考虑可能有助于我们象下图那样放置长度P，并且如果我们对作图题有些经验的话，大概不会忘记和ED 一起引入辅助线AD 和AE。毕竟，它们都是等腰三角形的底边。

观察这个图形，我们可以发现∠EAD 和角α 有关系：∠EAD = α/2 + 90°。知道这个特点后，我们很自然地会想要去作出△EAD（已知△EAD的底边ED的长度、高h 和∠EAD，利用正弦定理[两种形式，带h 的和不带h 的]+余弦定理，那么这个三角形是可解的，具体做法可以这样：任做一个满足角度关系的∠EAD，据此可以得到满足角度关系的A 点的轨迹——以ED 为端点的一段圆弧。该圆弧和平行于ED 并且与之相交为h 的直线的交点即为所求A 点。然后，取AE、AD 的垂直平分线，分别交ED 与点C、B，便可得到△ABC）。我们引入了一个辅助问题，它比原来的问题简单。

波尔查诺

"我根本不认为我在这里能够提出任何早先未曾为所有具有才华的人所察看出的研究过程；并且我也根本不想允诺你们可以从我这里发现这方面的很新颖的任何内容。但是，我将煞费苦心地用清晰的词句来说明所有有才能的人所遵循的研究规则与方法，这些有才华的人在大多数情况下，甚至不知道他们自己是遵循这些规则与方法的。虽然，即使正在做这件事的时候，我也不敢幻想我将会完全成功，但我仍然希望在这里所提出的一孔之见会博得某些知音并在以后有所应用"。

好念头

好念头是对解答突然有进展的一种口语描述。好念头的出现，每个人都体验过，但只能意会难以言传。所以提一提想亚里士多德这样古老的权威曾经给过一个很有启发性的描述，可能会使人感兴趣。大多数人会同意：想出一个好念头是一种"灵感活动"。亚里士多德对灵感所做的定义如下："灵感就是在微不足道的时间里，通过猜测而抓住事物本质的联系"。

你能检验这结果吗？

你能检验这结果吗？你能检验这论证吗？对这类问题若能给出很好的回答，将加强我们对答案的信任并巩固我们的知识。

考虑一个例子，一个底为正方形的棱台。设下底边长为a，上底边长为b，高为h，则其体积为（a^2+ab+b^2）h/3。

我们可以利用"特殊化"的方法来检验这结果。事实上，若a = b，则棱台成为棱柱，公式成为a^2h；若b = 0，则棱台成为角锥体，公式成为a^2·h/3。此外，我们还可以用"量纲检验法"，事实上，公式的量纲是长度的立方。还可以用数据的变化（我觉得不妨称其为放缩吧）来检验公式，事实上，若a，b 或h 中的任一个增大，则公式的数值也增大。

你能用不同方式导出这一结果吗？

就象我们期望通过两种不同的知觉去感觉一个物体一样，我们也期望用不同的推到方法去取得对对理论结果的有效性的信心。两个证明比一个好，"抛两个锚更安全"。

我们的问题是:已知正圆台的下底半径R，上底半径r 和高h，求其侧面积S。

该问题可用多种方式求解，一个可行的思路是，我们知道整个圆锥的侧面积公式：1/2*底周长*侧高，并且圆台是从圆锥切去一个较小的圆锥而得到的，所以它的侧面积是两个圆锥侧面积之差。于是剩下的工作就是把它用R、r、h 表示出来。再加上三角形相似的知识，我们可以得到终式：S = π(R+r)√[(R-r)^2+h^2)]。现学现卖，我们可以利用上一小节的检验方法验证公式的正确性，若R=r 则圆台成为圆柱，公式成为2πRh；若r=0 则圆台成为圆锥，公式成为πR√(R^2+h^2)。当然也可以用量纲检验、放缩等。但是，这里我们最好是能进一步发问：你能用不同方式导出这结果吗？你能一下子看出它吗？

为了更好的理解这个答案，我们可以从尝试看出其各个部分的几何意义开始。这样，√[(R-r)^2+h^2)] 可看作圆台斜高的长度；π(R+r) = (2πR+2πr)/2（或2π(R+r)/2）。找到各个部分的新解释之后，我们可以从不同角度来看整个公式，于是我们可以这样读它：侧面积 = 中截面周长*斜高。这里，我们可能回忆起梯形面积公式：面积 = 中线 * 高。

PS：我们称平行于圆台上底和下底并平分其高的平面与圆台的交为中截面。

你能利用这个结果吗？

我们可以通过"普遍化"、"特殊化"、"类比"、"分解和再组合"等方法来变化一个问题，从而由原问题导出别的问题。

当我们成功地解决了一个好问题以后，我们应当去寻找更多的好问题。好问题同某种蘑菇有些相像，它们都成堆地生长。找到一个以后，你应当在周围找找，很可能在附近就有几个。

对于从已有解的问题导出易解的新问题，这里有个模式（变换数据的地位）可以利用：我们设原来的未知数为已知，并将原来的已知数之一作为未知数。在这新、老两个问题中，联系已知数与未知数的关系式相同，在一个问题中找出关系式，我们即可把它用于求解另一个问题。

实现

尽可能形式地证明我们所直观看到的（一个聪明的学生，无须任何系统的立体几何知识，当他弄清楚名词术语之后，他立刻能看出平行于同一直线的两直线彼此平行，此三直线可以在同一平面上，也可以不在同一平面上，但证明这个命题则需要冗长、细致和创造性的准备工作。如欧几里得几何原本第11 分册命题9 所给出的那样），以及尽可能直观地看出我们所形式证明过的（逻辑规划与代数公式的形式演算比直观要深入得多。几乎每个人都可立刻看出：任取三条直线最多可将平面划分成7 部分，但是几乎没人能看出[即使他全神贯注、聚精会神地看]任意的5 个平面最多可将空间分为26 部分[注：类比是一个伟大的引路人，求解立体几何的问题往往有赖于平面几何中的类比问题。解决当前这个问题的一种方案是利用n 条直线最多将平面划分成几部分这个问题的结果和方法]）这是一种增进智力的练习。

条件

如果一个条件包含了过多的部分，则此条件称为多余的。如果一个条件的各部分互相矛盾并且互不相容以致无对象可以满足此条件，则此条件称为矛盾的。

这样，如果条件用比未知数个数多的线性方程来表达，则它不是多余就是矛盾的；如果条件用比未知数个数少的方程来表达，则它是不充分的，不足以确定未知数；如果条件用与未知数个数一样多的方程来表达，那么在通常情况下，它对于确定未知数正好是充分的，但在例外情况下，也可能是矛盾的或不充分的。

看起来有些绕人哈，看看下面的例子（阿基米德发现的东西，天才出题，智者解题：-），从里面绕出来，你就不觉得绕人了：

如上图，两个小圆互不包容，但是都在第三个大圆里面。三个圆两两相切，并且它们的圆心都在同一条直线上。已知较大的圆的半径r，两个小圆的公切线在大圆中的一段长为t。求在大圆内和两个小圆外的那部分面积。

感觉问题合理吗？条件充分吗？没有两个小圆的半径，我们不能确定它们的面积，那么所求的面积还可求吗？

提示[白色的，选中查看]：以S 代表所求面积，x 和y 代表两个小圆的半径，我们有：S = πr^2 - πx^2 -πy^2; 2r = 2x + 2y。由比例中项，或者相交线定理（两者利用相似三角形都很容易证得）得到(t/2)^2 = 2x · 2y。三个未知数三个方程，联立后面两个方程，得到x^2 + y^2 的值，带入第一个方程得到S = πt^2/8。

是不是觉得很有意思？我们开始觉得条件少，不足以确定未知面积，到最后却发现，条件竟然是多余的，也就是说我们可以保持t 不变，只改变r 的值，但是不管r 的值多少，只要t 不变，所求面积S 就不变。这个用软件模拟的方式应该可以直观地看出来。

推论

推论是一个定理，它是在研究一个刚求得的定理时很容易推出来的定理。推论（Corollary）这个字来源于拉丁文，一个更口语化的译法是"小费"或"酒钱"。

你能从已知数据导出某些有用的东西吗？

面对一个问解决的问题，我们必须找出已知与未知之间的联系。如果把待解的问题当作已知与未知间的一道鸿沟的话，我们需要做的就是在上面架桥。而架桥可以从已知或未知的任何一边开始。

看着未知数！试想出一个具有相同或相似未知数的熟悉问题。这是建议你从未知数开始进行工作。

看着已知数！你能从已知数导出什么有用的东西吗？这是建议你从已知数开始进行工作。

例：给定三点A，B，C。过A 做一线与B，C 等距离。

看起来做张图是有必要的：

此图未免太过空旷，似乎我们还需要某条辅助线，还要加点什么呢？一个高水平的学生对此也可能一筹莫展。当然，有各种办法可以尝试，但帮助学生重新振作起来的最好问题是：你能从已知事项导出什么有用的东西？实际上，已知是什么？就是上图的三个点，再没有别的了。我们迄今尚未利用过点B 和点C，我们必须从它们导出什么有用的东西。但是只有两个点，你能做什么呢？把它们用一条直线连起来！嗯，不错的想法，为何不试试呢？其实一旦你这么做了，就会发现问题的答案突然闪现出来了。这里有两个彼此全等的直角三角形，还有一个十分重要的新交点。所以所求是过A 点与BC 中点的直线。

你能重新叙述这个问题吗？

你能重新叙述这个问题吗？你能否重述得更不同些？提出这些问题的目的是找出合适的"变型的问题"。

回到定义去。

分解和重新组合

分解和重新组合是重要的智力活动。

从所提问题构造出一个新问题，我们可以：

• 保持未知数不变而改变其他（已知数与条件）
• 保存已知数不变而改变其他（未知数与条件）
• 只改变条件
• 同时改变未知数和已知数

例子：已知三角形一边a，垂直于a 的高h 和a 的对角α，做一个三角形。

我们可以尝试变换问题，把它化简为点的作图问题：新的未知是一个点A，老的未知是一个三角形。新的已知给定B 与C 两点。

下面我们给出一个一般化的解题模型——"双轨迹的模型"，依照它我们就可以在若干场合下成功地解决几何作图问题：

• 首先，把问题归结为要确定一个点
• 然后，把条件分成两部分，使得对每一部分，未知点都形成一个轨迹
• 最后，取两个轨迹的交点即为所求

这一模型就是一个典型的通过改变条件（对当前问题而言，即：保留一部分条件，而舍弃其余部分）构造新问题的模式。利用该模型我们首先把条件的各个部分分开：

1. 对直线BC 的距离为h
2. 顶点A 的角大小为α，该角的两边通过给定点B 和C

不难看出，条件1 中点的轨迹为一条平行于BC 且与之相距为h 的平行线；条件2 中的点的轨迹是端点为B 与C 的一段圆弧。画出这两个轨迹，它们的交点就是所求的点A。

关于双轨迹模型，我想举两个好玩的例子还是很有必要的：

问题1、三等分给定三角形的面积，即在给定三角形的内部求一点X，使得△XBC，△XCA 和△XAB的面积相等。

提示[选中查看，下同]：保留部分条件，而扔掉其余的条件：如果只要求△XCA 与△XCB 的面积相等，X 有怎样的轨迹？不难证明，X 的轨迹是过C 的中线，从而所要求的点乃是中线的交点；这里，再提供另外一种"双轨迹模型"的解法：如果X 的变化使得△ABX 的面积保持为△ABC 的面积的1/3，X 的轨迹是平行于AB 的直线，到AB 的距离等于从C 点引出的高的1/3，从而知所求的点是这些平行于边的直线的交点。

问题2、给定a，α，r 做是三角形。这里α 为边a 所对应的角度，r 是该三角形的内切圆半径。

提示：保留部分条件，而扔掉其余的条件：不考虑r，只保留a 和α，内切圆的中心有怎样的轨迹？连接内切圆圆心与边a 的两个端点，这样得到的三角形的以内切圆圆心为顶点的角是α/2+90°，因而其轨迹为关于线段a 彼此对称的圆弧，其公共端点是线段a 的端点B 与C。作平行于a 且相距a 为r 的直线，与方才得到的圆弧的交点即为内切圆圆心，然后过B、C 分别做内切圆的切线（过圆外一点做圆的切线的方法是：以该点和圆心的连线为直径做圆，与原先的圆交于两点，这两个点即为切点。原理就是直径所对的圆心角为90°），其交点即为A 点。

定义

一个术语的定义就是用其他假定已为人所周知的术语来阐明该术语意义的一个语句。如抛物线的定义：抛物线是距离一定点和一定直线距离相等的点的轨迹，该定点称为抛物线的焦点，而该定直线称为抛物线的准线。

例：已知抛物线的焦点和准线和一直线，求作此抛物线与已知直线的交点。

你能否通过画张图、引入适当的符号重新叙述这个问题？

如上图：我们可以将该问题重述为：在已知直线C 上做点P，使它和已知点F 及已知直线d 等距离。这样，我们就消去了专业术语。

为了消去一个专业术语只知道其定义是不够的，我们需要在定义的基础上引入适当的元素（就本例而言，决定性的一步是在图中引入直线PF 和PQ，根据抛物线的定义，这两者是相等的）。

回到定义去是一项重要的智力活动。如果我们希望了解为什么字的定义如此重要，那么我们应当首先认识到，字是重要的。如果不用字，不用符号或某种记号，我们几乎不能思维，它的威力在于其给我们提示的概念以及这些概念所依据的事实。

对于回到定义去，数学家寻求的是：掌握那些在专业术语后面数学对象间的实际关系；物理学家寻求的是：专业术语后面的明确的经验；而具有某种常识的普通人则希望找出铁的事实而不仅仅为字面所愚弄。

这里再放一题：过圆上任意一点做圆的切线，求切线的斜率。

提示[选中查看]：圆的切线是怎么定义的；多说一点，另一种方法可以直接利用圆的方程进行微分。比较一下两种方案，感觉初等和高等数学都能解决的问题，用初等的办法往往很简洁，但是思路相对高等的方法难找一些；而高等的方法往往很暴力，略微繁琐。

笛卡尔

笛卡尔写"方法论"与"法则"的动机：当我年青的时候，我听见有关天才的发明，甚至是我还没有读过作者的著作以前我就尝试自己去发明它们。这么做，我发现我在某种程度上利用了某些规则。

决心，希望，成功

教学生解题时意志的教育。当学生求解那些对他来说并不太容易的题目时，他学会了败而不馁，学会了赞赏微小的进展，学会了等待主要的念头，学会了当主要念头出现后全力以赴。如果学生在学校里没有机会尝尽为求解而奋斗的喜怒哀乐，那么他的数学教育就在最重要的地方失败了。

你是否利用了所有的已知数？

一个陈述完善而且合理的"求解题"必须具备所有必需的已知数，而没有任何多余的未知数；并且它的条件必须是恰好充分，既不矛盾，也不多余。在解决这样一个问题时，我们当然必须利用所有已知数和整个条件。

例：对一个已知长、宽、高分别为a、b、c 的长方体而言，其对角线长度为多少？

初次接触该问题的学生可能想到了怎样计算一个平面的对角线√(a^2+b^2)，然后他可能停滞不前了，教师可以通过这样提问来帮助他：你利用了所有的已知数吗？

你知道一个与此有关的问题吗？

我们几乎不能想象有一个问题是绝对的新颖，和我们以前解决过的任何问题都不相似，都无关系；但若居然有这样一个问题，它将是不可解的。事实上，当解决问题时，我们总利用以前解决的问题，用其结果或用其方法，或利用解决它们时所得到的经验。当然我们所利用的这些问题必须在某一方面与我们当前的问题有关。所以，我们提出这个问题：你知道一个与此有关的问题吗？

我们必须从想出的问题中找出与当前问题联系最密切的问题，我们看着未知数，或者我们寻找一个早已解决的问题，这个问题与我们当前的问题通过"普遍化"、"特殊化"或"类比"而发生联系。

我们这样做的目的是把以前所获得的知识调动起来。我们数学知识中的一个主要部分是以过去证明过的定理形式存储在我么大脑中的。所以有下列问题：你知道一个可能用得上的定理吗？当我们的问题是一个"求证题"（即必须证明或推翻一个提出的定理）时，提出该问题可能特别合适。

检验你的猜测

把一个逼真的猜测当作已被证明的真理看待同对一个逼真的猜测完全弃之不顾一样都是相当愚蠢的。

例：在周长一定的所有四边形中找出面积最大的一个。

这个问题和通常的初等几何问题很不相同，所以我们自然要从猜测开始。哪种四边形可能具有最大面积？最简单的猜测是什么？我们可能听见过在所有具有相同周长的图形中，圆的面积最大。现在，哪种四边形最接近圆？从对称性来看，哪一种最接近于圆？正方形是很自然的一种猜测。当我们有勇气写出：在所有周长一定的四边形中，正方形的面积最大。我们应当意识到情况的变化，我们的问题由原来的"求解题"，经过一番猜测后变成了"求证题"。问题似乎仍然很棘手。如果你不能解决所提出的问题，首先尝试去解决某个与此有关的问题。你能解决问题的一部分吗？如果正方形在所有四边形中面积最大，那么在长方形中它也必然如此。因此，如果你能证明"在所有周长一定的长方形中，正方形的面积最大"，那么我们将解决我们问题的一部分。这个定理看起来比前一个定理更好着手（更好着手的是：在周长一定的平行四边形中，长方形的面积最大），当然，它较弱。我们尚未解决我们的问题，但由于我们敢于面对我们颇为明显的猜测，我们得到某些进步。

图形

在研究作图问题时，假定条件均满足，画张草图，再开始研究这一方法可追溯于希腊几何学家。帕普斯有一句简短而有点高深莫测的话：设欲为之者如已为之。用现代话来说就是：画张假想的图，图中假定问题的各个部分都满足条件。

一个不精确的图形有时可能给出错误的结论，但这危险不大，而且可以用各种方法加以避免，特别是用变化图形的方法。如果我们集中注意力于逻辑联系，并且认为图形是一种辅助工具，决非我们结论的基础，而真正的基础是逻辑联系，那就不会有什么危险（这一点可由某些众所周知的悖论富有启发性地加以说明，这些悖论巧妙地利用了图形上故意画得不准确之处）。

嗯，我觉得举个例子更形象一些：

例：证明所有角都是直角（当然了，谬论啊。用下面的方法你也可以说所有角都是钝角或者所有角都是直角）。

如下图，在线段AC 上做AB = CD，并且使得∠BAC 为直角，∠ACD 为钝角。联结BD 并作其垂直平分线交AC 的垂直平分线于点P。下面我们要证明∠ACD = BAC。证明过程很简单，就是利用SSS 可得△BAP ≌ △DCP。则∠BAP = ∠DCP，同时∠CAP = ∠PCA。∴ ∠ACD = BAC。同样的方法，可以证明所有的锐角都是直角，于是所有角都是直角。

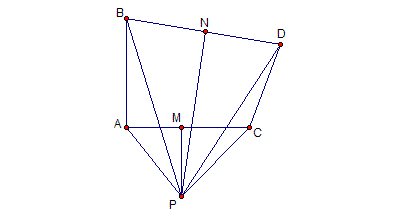
当然了，证明过程肯定出问题了，但是问题出在哪儿呢，你能不能看出来？

研究这个问题，我发现，其关键点在于：DP 是不可能与AC 相交的，通俗的说DP 一定在C 点的右侧。证明了这一点，原命题也就不攻自破了。

下面的解法，是我在解决这个问题时发现的（过程中发现并证明了几个"定理":D）：

利用特殊化的方法，我们使得原图中的AC 与CD 形成的夹角无限趋于180°，如下草图所示。首先，我们阐明一下LM、KM 的垂直平分线OO' 和PP' 的相对位置。首先，O 点在P' 点的右侧，这点由P' 是Le 的中点（因为由ASA 可得△LbP' ≌ △P'fe）可推得。同时P 点在OO' 的左上方，也就是说，OO' 和PP' 的交点在△LKM 的外部。这是为什么呢？因为LP < PM（LP=√(a^2+b^2)，PM=a+b。两边平方得LP^2=a^2+b^2，PM=a^2+b^2+2ab）。为什么LP 小于PM，就能断定P 点在OO' 左上方呢？注意到我在图中画的那个小三角形OBC 就是为了证明这个搞出来的。可以证明在△OAC 中，AC>OC-OA=OB-OA=AB，即如果A 点在底边垂直平分线的左侧，那么一定有AB<AC。反之亦成立（可以利用归谬法）。于是，我们推翻所有角都是直角这个谬论。

 

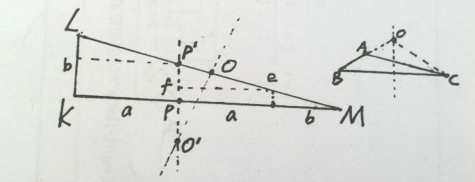
利用这种极限的特殊化方法，容易给人一种不正派、不正统的感觉，那么我们就来通过精细的作图来证明一下（再提一下：注意到这个特殊化带给你的启示，我们可以让那个钝角尽可能的大，我们可以取120°，虽然不是很大，但是比较特殊，方便我们求解PM。我们令a=b，可以求得LP=a√2，PM=a√3，即LP<PM 成立，同时它也不影响LM 的中点O 在P' 的右侧，这个特殊化就有说服力多了，它是实实在在的证明原先那个荒缪的问题是错误的一个反例，是不是有趣的紧啊:）：

(上图是我用动态作图软件GeoGebra 搞出来的。可以看到虚线在D 点的右侧。查看大图请点击这里。之前还写过一个基于斐波那契数列的谬论，详情参见这里。配合无字证明[这里]你有什么看法？）

此外，你的图形不应给出任何不恰当的特殊情况。图形的各部分不应当呈现出问题所未要求的明确关系。除非已有规定，线段不应看起来相等，或者垂直。如果三角形不是等腰的或直角的，就不能画得像等腰三角形或直角三角形。三个角为45°、60°、75° 的三角形，在文字的精确意义方面而言，是和等腰三角形与直角三角形的形状差别最大的。如果你想考虑一个"一般的"三角形，你可以画这样的三角形，或跟它差不多的三角形。

即使你的问题不是几何问题，你也可以试试去画张图。对于非几何问题，去找出一个清晰的几何表达方式，可能是走向解答的重要一步。

普遍化

普遍化就是考虑从一个对象过渡到考虑包含该对象的一个集合；或者从考虑一个较小的集合过渡到考虑一个包含该较小集合的更大的集合。

例一：如果我们碰巧遇到和数：1+8+27+64=100。你可能发现它可以表示成这样奇特的形式：1^3+2^3+3^3+4^3 = 10^2。现在，你自然要问：是否连续自然数的立方和1^3+2^3+...+n^3 都是一个自然数的平方？

我们提出这个问题，就是把问题普遍化了，这此普遍化是很凑巧的，它从一次观测到的事实引出显然普遍的规律。在数学、物理及自然科学中，许多结果是由这种凑巧的普遍化而发现的。

番外篇：我觉得这个问题是兼具普遍化与特殊化的绝佳的好例子，你会发现，对于刚刚得到的普遍化的命题并不很好证明，除非你把它特殊化：从1 开始的连续自然数的立方和等于其和的平方。除了数学归纳法以外，我们还可以利用指数比3 高一阶的二项式公式：(n+1)^4=n^4+4n^3+6n^2+4n+1 通过叠加求和来求解这个问题。这里有趣的普遍化问题又来了：你能求解n 个数的k 次幂的和吗（即：1^k+2^k+3^k+...+n^k）？

例二：给定一直线与一正八面体的位置。求过已知直线并二等分已知八面体体积的平面。

在求解题中，普遍化可能很有用（更普遍的问题可能更易求解，这看来矛盾，但该例表明了确实有这样的情况存在）。这个问题可能看起来很难，但事实上，稍稍熟悉正八面体的形状就足以提出更普遍的问题：给定一直线与一个具有对称中心的立体的位置，求过已知直线并二等分已知立体体积的平面。所求的平面显然经过立体的对称中心，所以这个平面应由这点与已知直线确定。由于我们把八面体有一个对称中心这个性质剖析出来了，所以我们原来的问题也就迎刃而解了。

你以前见过它吗？

你以前见过它吗？或者你是否见过相同的问题而形式稍有不同？为了得到解答，我们必须从我们的记忆中汲取有关的知识，我们必须调动起我们记忆中处于休眠状态的知识的有关部分。这样，在求解某一个别的问题时，曾经起过作用的特点在解决当前问题中还可能起作用。所以，当前问题的任何特点，如果它给我们的印象表明它可能是重要的，那么我们就应当尝试去认识它。它是什么？你熟悉它吗？你以前见过它吗？

这里有个与你的问题有关且早已解决的问题

利用某个早已解决的问题的意图会影响我们对当前问题的理解，试图把新老两个问题联系起来，我们就在新问题中引入一些元素，它们对应于老问题中某些重要的元素。例如，我们的问题是确定外接于已知四面体的球。这是个立体几何问题。我们可能回忆起，我们解过平面几何的类似问题，即作已知三角形的外接圆。于是，我们回想起，在平面几何这一老问题中，我们曾使用过三角形的边的中垂线。在我们当前这个问题中，应当试图引入某些类比的东西。这样就可能使我们想到在当前问题中引入四面体的中垂面作辅助元素。有了这个念头，仿照平面几何中的类比问题，我们很容易得到立体几何问题的解。

这里有一个定理与你的问题有关且早已证明过。这是上述讨论的变型。

探索法

探索法的目的是研究发现和发明的方法和规律，在试图建立探索法体系方面最著名的是笛卡尔和莱布尼兹，这两人都是伟大的数学家和哲学家。

如果你不能解决所提出的问题

你能不能想出一个更好着手的有关问题？现在你应该发明一个问题，不仅仅是回忆起一个。对于后者，当我们问：你知道一个有关的问题吗？的时候，我们已经尝试过了。

总之，如果原问题看来不可解，那么你应当尝试变化问题。变化问题有多种方法。如"普遍化"、"特殊化"、"类比"以及其他属于"分解与重新组合"的各种办法。

归纳与数学归纳法

归纳法是通过对特例进行观察与综合以发现一般规律的过程。它用于所有科学。

数学归纳法则仅在数学中用以证明某类定理。

还是拿"普遍化"小节中的例一做例子：如果我们碰巧遇到和数：1+8+27+64=100。于是把各个数写成平方和立方，我们得到了一个更有趣的形式：1^3+2^3+3^3+4^3 = 10^2。怎么会有这种事发生？我们不禁要问是否从1 开始的连续自然数的立方和都是一个自然数的平方？是否经常有这样的事？对于这个问题，我们能做什么呢？我们可以研究其他特例，得到表：

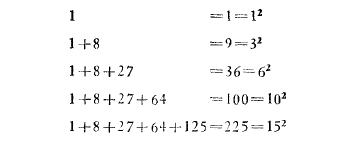
似乎很难相信，所有连续自然数的立方和是某个自然数的平方，这一事实仅仅是巧合而已。看来，我们似乎可以归纳出一个一般性的规律：

推论1：:前n 个自然数的立方和是一个自然数的平方。

我们不妨对猜测进行更深入的检验，尝试去剖析出更深刻的规律性。细心研究，不难发现表中的相邻两项之差本身（平方的底数）也是增加的：3-1=2，6-3=3，10-6=4，15-10=5。如此，在数字1，3，6，10，15 中，我们可以看出明显的规律性：

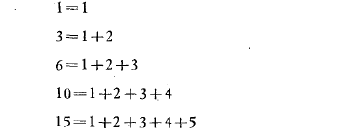
如果这种规律性是普遍的（而相反的情况是难以置信的），则我们所猜测的定理将有一个更精确的形式：

推论2：对于n=1,2,3,...  1^3+2^3+3^3+...+n^3=(1+2+3+...+n)^2。

我们已经发现了一个有趣的结果，但其论证仅仅是似乎有理的，实验的，假设的，探索性的。让我们尝试用严格的证明来把它肯定地建立起来。我们面临一个求证题，证明或推翻推论2。或许你知道1+2+3+...+n=n(n+1)/2。不管怎样，它是容易证明的，倒叙相加或是取一边长为n 与n+1 的长方形，用波折线把它分成两半，下图是n=4 的情况。

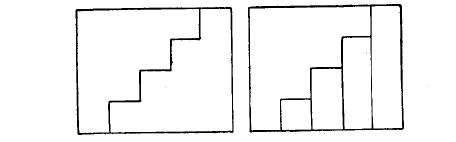
这样，我们将推论2 又变换为：1^3+2^3+3^3+...+n^3=[n(n+1)/2]^2。相信你用数学归纳法（其实它更精确的名字应该叫"从n 到n+1 的证明"或"过渡到下一个整数"，无奈，大家普遍愿意接受更加高大上的术语：-）可以很容易地证明这个等式的正确性。

这里还有一点，虽然微小，但对任何期望自己去证明的人来说却很重要。在前面，我们通过观察与归纳，找到两个不同的推论，后者比前者更精确。在讨论推论2 时，我们发现有检验从n 过渡到n+1 的可能性，于是我们能够用数学归纳法找到一个证明。如果讨论第一个推论而不考虑由第二个推论所添加的精确性，我们就几乎不可能找到这样一个证明。事实上，第一个推论不及第二个精确、明显、明确、易试验和易检查。从第一推论过渡到第二推论，从比较不精确的陈述过渡到精确的陈述是为最后证明所作的一种重要准备。

上述情况有矛盾的一面。第二个推论更强些，它直接蕴含着第一个，而多少有点"含糊"的第一个推论却几乎不蕴含更"清晰"的第二个推论。这样，更强的定理却比较弱的更易掌握，这是"发明家的矛盾"。

发明家的矛盾

雄心大的计划，成功的希望也较大。这看起来矛盾，但当从一个问题过渡到另一个，我们常常看到，新的雄心大的问题比原问题更容易掌握。较多的问题可能比恰好只有一个问题更容易回答。较复杂的定理可能更容易证明，较普遍的问题可能更容易解决。

总计，雄心大的计划可能有更多的成功机会，如果它不是仅仅根据浮夸，而是立足于看到某些表面以外的东西。

能满足条件吗？

是否可能满足条件？条件是否充分，足以确定未知数？或者它不充分吗？或是多余吗？或是矛盾吗？

莱布尼兹

没有什么比看到发明的源泉更重要的了。就我看来，它比发明本身更有趣。

引理

引理的含义是辅助定理，源于希腊语，可直译为"假设是什么"

比如我们打算证明一个定理A。过程中我们被引导猜测另一个定理B。若B 为真，我们也许能用它来证明A，我们暂时假定B 成立，把它的证明推迟一下，而先去证明A。这样一个假设的定理B 就是原来所提定理的辅助定理。

看着未知数

尝试想起一个具有相同或相似未知数且早已解决的问题（具有相同或相似结论且早已证明的定理）就会有一个好机会沿正确方向看是我们的工作，并且可能设想出一个解题计划。

尝试去重新回忆具有相同未知数的问题是个显而易见的常识性的手段。然而，如此简单有用的手段并非普遍为人所知。无论如何，不论是教师还是学生都不能不重视正确利用下列建议：看着未知数！尝试想起一个具有相同或相似未知数的熟悉问题。

符号

图及符号和数学思维有密切的联系，使用符号对于运用推理来看是必不可少的。

一个好符号应该是不含糊的、富有意义的、便于记忆的；他应该避免有害的第二重意义而利用有用的第二重要意义；符号的次序与联系应提示事物的次序与联系。一个好符号应便于记忆并便于确认，符号应使我们立即想起对象是什么，而对象则使我们想到符号是什么。

用广泛讨论公式性质的办法来检验一个公式，是一种特别有启发性的练习，并且使学生有充分的机会亲身体验到"数学符号语言有助于思维"。

拘泥与精通（重要，关于如何使用"怎样解题表"的说明）

这是对待规则的两种相反的态度。

• 不论场合是否合适，不折不扣地、刻板的、不加思索地应用某一规则，这是拘泥迂腐。某些拘泥的迂夫子是可怜的傻瓜；他们自始至终没有理解他们如此不分青红皂白，亦步亦趋地照办的规则。有些"迂夫子"则很成功，他们理解规则，至少在开始时（在成为迂夫子之前）理解，并且他们作出了适合于许多场合而只偶然失利的良好选择。应用规则要得心应手，运用自如；并且注意到规则所适用的场合，有选择、有批判地加以应用；不为规则的词句而迷失本意，或本末倒置或坐失良机，这就是精通。
• 文首关于问题与建议的表，对解题者和教师可能都有帮助。但是，首先必须了解这张表，学习怎样正确地应用这些问题与建议，并且通过试验与错误、成功与失败、通过应用来学习这张表。其次，决不可拘泥迂腐地应用它们。你不应当按照某种刻板的习惯，不加选择地提出问题和作出建议。需准备各式各样的问题和建议并作出判断。你正在做一件艰巨而又令人兴奋的工作；你下一步将要干什么应当根据对你当前的问题作仔细的、无偏见的考虑后再来决定。你希望帮助一个学生，你对你的学生说些什么，应当从同情并了解学生的困难这点出发。但如果你喜欢当一名迂夫子而必须依靠某种规则，请学习这一条：永远要先开动自己的脑筋。

实际问题

实际问题在许多方面与纯数学问题不同（在实际问题中，未知数、已知数据、条件、概念、所需要的预备知识，每项都比纯粹的数学问题更复杂，更不清楚。这是主要的差别，但它肯定还包含更多的差别），但求解的中心思想与程序基本上相同。实际工程问题通常包含数学问题。

在一个陈述的数学问题中，所有已知数据与有关条件的所有条款都是必不可少的，从而必须加以考虑。在实际问题中，我们有大量的已知数据与条件，我们力求尽可能多的加以考虑，但我们却不得不忽略一部分。就拿大坝设计者为例来说吧，他考虑了公众的利益和重大的经济利益，但他不得不舍去次要的要求与损害。严格来说，他问题中的已知数据是数不胜数的。例如，他可能愿意多了解一些地基的地质性质，但他最后毕竟必须停止收集地质数据，虽然不可避免的仍然有一些不清楚的地方。

求解题，求证题

求解题的目的是找出某个对象，即问题的未知数。求证题的目的是最终说明某个清晰陈述的推断是成立还是不成立。

在初等数学中，求解题更重要。在高等数学中，求证题更重要。

进展与成就

趋向解答的进展是什么？进一步动员（为了解题，我们必须具备本论题方面的知识并且必须对我们现有的，但原来处于休眠的知识进行挑选并收集相关内容。从我们的记忆中汲取这些有关内容可称之为"动员"）与组织（为了解题，仅收集孤立的事实是不够的，我们还必须把这些事实组合起来，并使之比较适用于我们手头的问题。这种加以组合和使之适用的活动可称之为"组织"）我们的知识，改进我们对问题的理解，增加我们对构造最终论证的步骤的预见性，这些都是进展。我们可能以难以觉察的小碎步缓慢前进，但时而又飞腾跳跃突飞猛进。向求解的突然进展我们称之为好念头。什么是好念头？是我们观念上的一次重大突变，我们看问题方式的一个骤然变动，在求解步骤方面的一个刚刚露头的有信心的预感。

我们表中的问题和建议并不直接提到好念头。但实际上，所有的问题和建议都与它有关。了解问题是为好念头的出现作准备；制定计划是试图引发它；在引发以后，我们实现它；回顾此过程和求解的结果，我们是试图更好的利用它。

归谬法与间接证明

归谬法和间接证明是两种不同的，然而相互关联的过程。

归谬法是利用导出一个明显的谬误来证明假设不成立。间接证明是通过证明相反的假设不成立来证明某个推断成立。

归谬法与间接证明都是发明创造的有效工具，这些发现创造是在一个专心致志的头脑中自然涌现出来的。

• 归谬法

例1：在0，1，...，9 这10 个数字中，每个都要用一次且只允许用一次，写出几个数（可任意组合，如：39、28、46、50、1、7）使得其和数为100。

在多次尝试都是得到99 之后，自然地，我们可能产生怀疑：按照所要求的方式是否不可能得到100？因此，我们的脑海中涌现了问题：证明所提条件的两个部分不可能同时满足。

即使是十分优秀的学生也可能感到这个问题超出了他们力所能及的范围。但如果我们有正确的态度，并不难回答。我们想象有一组数，其和为100。它们必定是一些有一位或者两位数字的数。而且尤为重要的一点是这10 个数字的和为45。这些数字，有的用来表示个位数，有的用来表示十位数。我们令t 表示十位数的数字之和，则其余数字表示个位数，其和为45-t。因此，这组数之和必为10t+(45-t)=100，即t=55/9。注意到，t 竟不是整数。如何解释这一点呢？我们原先的假定一定是错误的，即条件的两部分不能同时得到满足。

• 间接证明

例2：证明质数有无穷多。

我们假想存在一个最后的质数P。于是我们可以写出整个质数序列：2，3，5，7，11，...，P。为什么这是不可能的呢？它错在哪儿？我们能否指出任何肯定的错误？确实，我们能够。我们可以构造一个数Q=2·3·5·7·11···P+1。该数大于最后一个质数P，由此可断言，Q 不可能是一个质数。因此Q 一定能被质数除尽（根据算术基本定理）。然而，根据根据前面的假设，Q 被其中任何一个质数除时，都有余数1，即Q 不能被上述任何一个质数除尽。因此Q 一定是一个质数。现在好了，从存在一个最后的质数这一假定出发，我们已经引导出一个明显的错误：Q 即是又不是质数。怎么解释这点呢？我们原来的假设一定是错误的。即并不存在一个最后的质数P，于是我们成功地证明了质数的序列永不终止。

我们已经建立了我们的定理（质数序列用不终止）。这是通过反驳其对立面（质数序列终止与某数）而得到的，即从对立面引出一个明显的谬误。这样，我们已经把间接证明和归谬法合并在一起了，这种合并也是非常典型的。

与其它科学类似，数学发展到现在，分支众多，自然少不了分歧。例如大数学家布劳威尔发展了构造性数学，它不承认无穷集合（康托尔证明了实数比自然数多）。只承认构造性的证明而不承认排中律，也就不承认反证法（间接证明常常运用反证法，并且反证法常常利用归谬）。但这并不影响我们从刚才两个问题中得出的结论的正确性。事实上，我们能够改造它们，用不同的方式导出这个结果——对例1 而言，可以这样说，9(t+5) 可被9 除尽，而100 不能被9 除尽，因此该和数不可能为100。对于例2，我们可以把求证题化为一个求解题：给定从最小质数2 开始的连续序列2,3,5,...,P，求一个新质数N 与所给定质数不同。

发明创造的规律

发明创造的规律，第一条是动脑筋和运气好；第二条是锲而不舍直到一个好念头出现。

企图发现指引人们去解答所有数学问题的这种放之四海而皆准的发明创造规律是不切实际的。

合理的探索法不能以万灵规律为目标，但它可以努力研究在解题中典型有用的做法（智力活动，策略，步骤）。这种做法是每一个对他的问题很感兴趣的正常人所检验过的。这些人被提示以某些固定格式的问题与建议（聪明的人是自己向自己提，学生则由老师向他提）。收集这类问题与建议并使其具有充分的普遍性并且安排简洁得体，这虽不及点金石那样使人向往，但却切实可行。文首中的表就是这样的内容。

建立方程

建立方程的意思是把用文字表达的条件改用数学符号来表示，它是从普通语言到数学公式语言的一种翻译。在建立方程中所可能遇到的困难是翻译的困难。

在建立方程之前，我们必须了解条件，把条件的各部分分开，并且问：你能写出它们吗？

例：已知一直线及一点的坐标，求一点与已知点对称与已知直线。

未知是什么？一点，设其坐标为(p, q)。已知是什么？直线方程，设为y=mx+n；一点，其坐标为(a, b)。条件是什么？点(a, b) 与(p, q) 彼此对称于直线y=mx+n。

通过把条件分为几部分、回到对称的定义去、什么样的几何关系可以在解析几何中表达的很简单，这样的问题，我们不难找到解决问题的简单可行的方案——连结已知点与所求点，使得连结它们的线垂直于已知直线（(q-b)/(p-a)=-1/m），并且，此连线的中点在已知直线上（(b+q)/2=m(a+p)/2+n）。两个未知数，两个方程。因此联立以上两式即可得到对称点的坐标。

特殊化

特殊化是从考虑一组给定的对象集合过滤到考虑该集合中的一个较小的集合，或仅仅一个对象。特殊化在求解问题时常常很有用。

例1：证明或推翻.在一个三角形中，令内切圆的半径为r，外接圆的半径为R 和最长的高为H，则r+R≤H。

所提定理属于不常见的一种。我们几乎想不起任何有关三角形具有相似结论的定理。如果什么也想不起，我们可以试验一下这个陌生推论的某个特殊情况。最熟知的特殊三角形是等边三角形，对于它，易证得r=H/3、R=2H/3。所以，在该特殊情况下，上述推论是正确的。继续实验等腰三角形这一较一般的特例。等腰三角形的形式随顶点处的角度而变化。它有两个极限情况，一个是顶点角为0°，另一个是180°。在第一个极限情况中，等腰三角形的底消失了，显然有r=0，R=1/2H 于是，推论得到证实。但是，在第二个极限情况中，所有三个高都消失了，而r=0，R=∞，H=0。上述推论并未得到证实。于是，我们已经证明了所提定理不成立，这就解决了我们的问题。

不过，由于对于非平常的顶角接近180°的等腰三角形，上述定理不成立。所以，我们可以"正式"地舍去上述极端情况，考虑这些极端情况不那么"正统"。循着刚才第二种极限情况带过我们的启示，我们可以搞一个特殊点的钝角等腰三角形。于是，我作了下图，一个底角为30°的等腰三角形。由图可得，H=√3，R>√3，我们甚至不用求r（相对麻烦，要利用解析几何来建系求解），便推翻了所提定理。

例2：已知两船的速度及其在某一时刻的位置；两船各以匀速直线航道行驶。求当两船相距最近时，彼此之间的距离。

下面，让我们画张图，并引入适当的符号。如下图，把船A 与B 看出质点，向量AP 及BQ 代表给定的方向和速度。

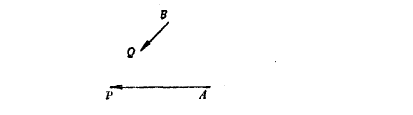
现在，如果我们只希望用初等方法，则可能仍束手无策。问题不太容易，但是其困难有某些特色，不妨将其表达为"变化太多"。A 与B 的初始位置和速度、行驶方向都可用不同的方式给定。事实上，四点A、B、P、Q 是可以任意选择的。现在，不论已知数据是什么，所求解答必须能适应任何一种情况。而迄今为止，对于找到这样一个普适的解答我们似乎毫无头绪。出于"变化太多"这样的感觉，下述问题与解答可能终究会涌现出来：你能不能想出一个更好着手的问题？一个更特殊的问题？当然，有极端情况，例如其中有一个速度为0（B 点的船可以抛锚，于是Q 与B 重合）。如果上述念头出现时，预感到"前面路还远"，但又感到该极端特例会起某些作用——则这个念头确实是一个好念头。这里有一个与你的问题有关的问题，就是你刚刚解决的那个特殊问题。你能不能利用它？你能不能利用它的结果？为了能利用它，你是否应当引入某个辅助元素？仔细想想，怎么才能把B 停止不动这一情况运用到B 向前移动的情况中去呢？停止不动是运动的特例，而运动是相对的，所以，不论B 的给定速度是多少，我们都可以把B 看作是停止不动的。下面让我们更清楚地表述一下这个念头：如果我们由两只船所组成的整个系统具有同一个均匀速度（有大小有方向），则两船的相对位置不变，相对距离不变，特别是问题所求的两船的最短相对距离也保持不变。现在，我可以加上一个运动，把其中一个船的速度减为零0，这样就把问题的普遍情况简化为刚才解决的特殊情况。让我在BQ 与AP 上加上一个与BQ 方向相反，大小相等的速度。这是个辅助元素，它使我们可能利用特殊结果。做出最短距离BS，如下：

我们成功地解决了我们的问题主要归功于两点。第一，我们想出了一个有利的辅助问题。第二，我们发现了一个从辅助问题过渡到原问题的补充说明（关于运动的相对性）。

特殊化还有许多其他用途，比如，它在检验结果方面也是有用的。

还想在这里补充一个问题——一个一般和特殊的等价关系。如：二项式定理，对于未知的x 和任一非负整数n，有：(1+x)^n = C(n,0) + C(n,1)x + C(n,2)x^2+ ... +C(n,n)x^n（可以由数学归纳法证明这个定理），你能从这个特殊情况，证明更为一般的二项式定理恒等式吗？(a+b)^n = C(n,0)a^n + C(n,1)[a^(n-1)]·b + C(n,2)[a^(n-2)]b^2 +... + C(n,n)b^n。

提示[又一次，白]：令x = b/a，则a^n(1+x)^n = (a+b)^n。特殊的和一般的这种等价，在哲学家和初学者看来也许是令人费解的，但是，这种东西在数学上却很平常，该如何解释这点不同呢？

潜意识的工作

如果你是一个热心的解题者，你在解题方面大概有类似的经验：常常会出现这种情况，你对一个问题束手无策，你奋力工作，然而毫无进展。但当你休息一夜或者中断几天之后，突然出现了一个好念头，问题便迎刃而解了。

这类偶然发生的事给人的印象是潜意识工作。它给我们带来的启示就是，某些时刻，我们最好暂时把问题束之高阁。"谋之于枕"是一句古老的忠告。稍事休息后，我们可能事半功倍。"今日不成，明朝可能"是另一句古谚。然而我们绝不应该把将来还要回过头来搞的问题没有什么进展就搁置一旁，当搁置这个问题时，问题至少应当解决了一些，在某个方面有所澄清。

只有那些我们热切希望求解或者我们曾经为之十分紧张地工作过的问题重新拿起时才有所进展。看来，为使潜意识工作，主观意识的努力与紧张是必不可少的。如若不然，问题未免过于轻而易举了，因为我们只要睡上一觉，袖手等待一个好念头便可解决了棘手问题。

自古以来，我们总把突然而来的好念头看成一种灵感，一种上帝的恩赐。你必须工作或者至少有强烈的愿望，才配得到这种恩赐。

聪明的读者、教师、作者

一本数学书的聪明的读者希望两件事：

• 第一，看出当前这步论证是正确的；
• 第二，看出当前这步论证的目的。

聪明的教师和教科书的聪明作者（国内那些垃圾教科书的作者真该好好跟Polya 学学，什么高等数学啦，线性代数啦，概率论与数理统计啦，恶心翔一般的感觉）应当把上述观点牢记心头。正确的写与讲肯定是必要的，但还不够。如果在书中或黑板上的推导很正确，但接连几步的目的难以理解（或猜不出任何理由），如果读者或听众不能理解怎样才能在力所能及的范围内找出这样一个论证，如果不能从推导中得到他如何找出这样一个论证的启示，那么这种推导是难于接受和无教益的。

聪明的解题者

聪明的解题者经常问自己那些类似于我们的表中的问题。他大概自己发现过这类问题；或者从别人那里听到过这样一个问题，然后自己发现了其恰当用法。他再三重复同一个刻板定型的问题可能完全出于不自觉。他知道该问题是他智力活动的一部分，适合于工作的这样和那样的阶段，于是他通过提问正确的问题，唤起正确的智力活动。

聪明的解题者会发现我们表中的问题与建议很有用。然而他并不能真正的理解，除非他亲自碰到过该问题在他工作中所试图引起的做法，同时在体验了问题有用以后，亲自发现了其正确用法（不去实践的思考永远都是浮于表面的）。

聪明的解题者应当准备好提问表中所有的问题，但是只有当他仔细地考虑过手头的题目并且经过他自己不抱成见地判断之后他才能提问题，否则一个问题也别问。事实上，他必须亲自识别当前情况是否与他过去成功地应用该问题的其他情况相类似。

聪明的解题者首先要力争尽可能彻底而又清楚地了解题目。可是仅仅了解还不够，他必须全神贯注于该题，他必须渴望得到解答。如果他不能激发真正的解题愿望，他最好将该问题束之高阁。真正成功的公开秘诀是：把你的全部身心投入到你的题目中去！（不只是题目，感觉具有普适性:）

未来的数学家

未来的数学家应当是一个聪明的解题者，但仅仅是一个聪明的解题者还不够。他应当发现自己的爱好与厌恶、他的情趣和他自己的擅长，应力争做出他的第一个重要发现。

对于他，工作中最重要的一部分是回顾已完成的解。在研究他自己的工作过程和解答的最后形式时，他可能发现需要观察的事物真是形形色色、无穷无尽。他可以沉思问题的困难所在以及关键性的念头是什么；他可以试图找出究竟是什么阻碍了他，是什么最后帮助了他。他可以寻求简单的直观概念：你能不能一下子看出它？他可以比较与发展各种方法：你能不能用不同的方法导出这结果？他可以尝试把当前的问题与一个早已解决的问题相比较从而澄清当前的问题；他可以尝试去发明新问题，而这些新问题可以在他刚才完成的工作基础上加以解决：你能不能把这结果或方法利用到某个其他问题上？对他所解决的问题尽可能完全的消化吸收、融会贯通，则他可以得到井然有序的知识，以备随时应用。

问题的变化

解题中的成功有赖于选择正确的方面，有赖于从好接近的一侧攻击堡垒。为了找出哪个方面是正确的方面，哪一侧是最好接近的一侧，我们从各个方面、各个侧边去实验，我们变化问题。从某种观点来看，解题中的进展可以看作是对早先获得的知识进行动员与组织的结果。变化当前的问题，有利于我们从记忆中汲取某些元素放进当前的问题中。

我们记忆事物是通过一类被称为"内心联想"的"接触活动"来进行的；我们现在脑中的事物倾向于使我们回想起过去曾和这事物接触过的东西。变化问题使我们引进了新的内容，从而产生了新的接触，产生了和我们问题有光的元素接触的新可能性。

例1：已知棱台的底面是正方形。下底边长为a，上底边长为b，棱台的高为h，求棱台的体积。

如果你冥思苦想丝毫没有进展，可以从变化问题的已知数开始。我们现在从a>b 的棱台开始。当b 增加到与a 相等时会出现什么情况？棱台会变成一个棱柱，而体积成为a²h。当b 减小到0 会出现什么情况？棱台将成为一个棱锥，而且体积成为a²h/3。这种已知数的变化，首先可以引起对问题的兴趣。其次，它可以提示我们去以这种或那种方式利用上面所提到的关于棱柱与棱锥的结果。无论如何，我们已发现了我们最后结果的明确性质；最终的公式必须是这样，当b=a 时，它化简成a²h，当b=0 时，化简成a²h/3。预见到我们打算求的结果具有什么性质这是一大长处。这种性质可以提示有价值的建议，而在任何情况下，当我们找到最后的公式时，我们可以借助这种性质来检验公式。这样，我们就预先回答了下述问题：你能检验这结果吗？

例2：已知梯形的四个边a，b，c，d。作出此梯形的图形。

我们令a 为下底，c 为上底；a 与c 平行但不相等，而b 与d 不平行。如果没有别的念头出现，我们可以从变化已知数据开始。我们从一个a>c 的梯形开始。当c 减小到0 时发生什么情况？梯形退化成三角形。三角形是一个熟悉而又简单的图形，我们能用各种数据作图。把这个三角形引进我们的图中可能会有某些好处。我们只引入一根辅助线——梯形的一根对角线，便引进了这个三角形，如下图所示。

但我们审查这个三角形时，却发现它几乎没有什么用处；我们已知其两边a 和d，但我们应该有三个数据才能作图。让我们试试别的。当c 增加到等于a，会发生什么情况？梯形变成一个平行四边形。我们能利用它吗？稍加审视，我们就会注意到在画平行四边形时，在原梯形图上附加的那个三角形。这个三角形很容易作图，因为我们知道三个数据：其三边b，d 和a-c[注:可以用尺规做出这个三角形来，首先做出一边a-c，然后以其两端端点为圆心先分别以长度b 和长度d 为半径作圆，取两圆两个交点中的任意一个作为三角形的一个顶点，连结该顶点和线段a-c 的两个端点便可得到所需三角形；古代尺规作图的要求比较苛刻：直尺无限长但是没有刻度，它的用途就是连接点；圆规可张开无限宽，但是一旦提起来会自动合上，也就是不能通过圆规直接转移长度（古人是有很智慧的，可以间接地通过作图实现长度的转移，参见几何原本第一卷第二个命题）]。

变更原问题（作梯形）后，我们得到一个更好接近的辅助问题（作三角形）。利用辅助问题的结果，我们很容易地解决了我们原来的问题（但必须完成平行四边形）。

我们第一次尝试失败了。但回顾整个解题过程，可以看出第一次尝试并非如此无用。在其中含有某些念头；特别的，它给我们一个机会去想起用三角形作为达到目的的手段。实际上，我们是通过修改第一次不成功的实验才达到第二次成功的实验的。我们变更c：先实验把它减小，然后实验把它增加。

如以上例子所述，我们经常需要通过试验的手段对问题作各种修改。我们必须一再地变化它，重新叙述它，变换它，直到最后成功地找到某些有用的东西为止。我们可以从失败中学习，在不成功的实验中可能存在有好念头，并且我们通过修改一个不成功的试验可以达到一个较成功的试验。在各种试验以后，我们经常得到一个更好下手的辅助问题。一些典型有用的变化问题的模式有：回到定义去、分解与重新组合、引入辅助元素、普遍化、特殊化、类比等。

我们在解决问题时，如何正确地使用文首的那张表呢？当我们进展顺利时，当新的标记自动涌现时，如果拿一些多余的问题妨碍我们的自然进展，简直是愚蠢。但当我们进展不顺利，想不起什么念头，我们则有对问题感到厌倦的危险。这时正是去思索某个有帮助的一般性念头、或思索表中哪个问题与建议可能合适的好时机。而任何一个可能指明问题新方面的问题，都值得欢迎；因为它引起我们的兴趣，可以使我们继续工作、继续思索。

未知数是什么

未知数是什么？已知数据是什么？这些问题对解题者至关重要。他检验自己对问题的了解，他集中注意力于题目的这个或那个主要部分。解答，本质上就是把未知数和已知数据联系起来。所以，解题者必须再三集中注意力于上述元素。题目中可能有许多未知数，或者是条件可能具有必须分开考虑的各个部分，或者我们希望考虑某个已知数据本身。因此，我们可以利用上述问题的各个变型，如未知数是些什么？第一个已知数据是什么？第二个已知数据是什么？条件的各部分是些什么？条件中第一个子条件是什么？

上述问题主要针对求解题，而对于求证题，我们可能需要变化下问题：前提是什么？结论是什么？你假设了什么？你的假定中的各部分是些什么？

为什么要证明？

为什么我们要学习证明或教授证明呢？何者更为可取？是完全不证明还是每点都证明？还是有的证，有的不证？如果只是有的证，有的不证，应证明哪些？

• 完全证明

　　似乎很难理解我们是如何得到一个严格的"完全证明"（某类逻辑学家认为，想成为一个证明，必须不留空隙，没有破绽，也没有任何不肯定性，否则它就不是证明）这个概念的，因为在我们的日常生活中，或法律程序中，或在物理科学中，几乎找不到符合如此高标准的一个完全证明。带点夸张的说，人类是从欧几里得和他的著作《几何原本》中学到这个概念的。学习平面几何原理提供了得到严格证明这一概念的迄今最好的机会。如果普通教育打算给学生以直观证明与逻辑论证的概念，那么就必须重视几何证明。

　　举一个例子：在任何三角形中，三角之和等于两个直角（《几何原本》第一卷命题32）。证明方法我们在初中就学习过，过任意一个顶点作对边的平行线，根据内错角相等，我们知道，包含该顶点在内的三个角为一个平角，于是明命题得证。

• 逻辑系统

　　正如欧几里得《几何原本》所表明的那样，几何学并非仅仅是事实的一种汇集而是一个严密的逻辑系统。定义、公设、公理、命题并非随机安排的，而是按一种完美的顺序，使得每一命题能以前面的定义与命题为基础。命题以方式安排所组成的逻辑系统可以看成是《几何原本》一书的主要优点。几何体系是通过证明的"粘合"而成的。每个命题与前面的定义、公理以及命题借助于一个证明而联系起来。不了解这种证明，就无法了解这体系的本质。还是那句话，如果普通教育打算给学生以逻辑体系的概念，它必须重视几何证明。

• 助记体系

　　Polya 并不认为直观证明、严格论证和逻辑体系（我认为了解一些无字证明[请戳这里]和几何学谬论会增强对这几点的认识，前面我已经整理了这一部分，私以为无字证明在某种程度上可以看成一种助记体系，并且能够启发应当如何进行逻辑严密地论证）对任何人是多余的。我们欢迎把事实简单地、自然地、合适地结合起来的任何一种联系。这种体系并不需要建立在逻辑基础上，它只需要设计成能有效地帮助记忆即可。然而，即使一般化的逻辑概念没有什么特殊重要性，证明作为助记方法也可能是有用的（例如，学习关于三角形之和这一事实以及关于内错角的另一事实，难道有比下图更简单、更自然、更有效地帮助我们记住这些事实的方法吗？）。

• 菜谱体系

　　证明还有很多好处，但是并不鼓吹所有的证明都应该"详尽"地给出，比如对工程专业的学生教授微积分。工程专业的学生学习微积分乃着眼于应用，而且它们即无充分的时间，也无充分的训练和兴趣来和冗长的证明打交道或赞赏其技巧精微之处（如果按照严格的标准讲授微积分，则其证明要求有一定的难度而且技巧精微）。所以授课者不免强烈地倾向于把所有的证明都割爱。但这样做，就把微积分降到菜谱的水平了。菜谱可以完全为其目的服务。实际上，他并不需要任何逻辑体系或助记体系，因为其配方是其印刷文字而并非保留在记忆之中（解释了为什么考完大学数学后我们都忘了怎么炒菜了，就是不长炒吗，而且不了解原理地炒也没咩意思：-）。

　　但是，如果一本微积分的作者或者一位大学教师过分遵循菜谱体系，则它几乎不能为其目的服务。如果他只教方法，不教证明，则那些无吸引力的方法不能被人理解。若他只给出规则而不讲理由，则干巴巴的规则会很快被遗忘。数学不能用品尝点心一模一样的方式来尝试；但是，如果所有论证都被拒之于课堂之外，则微积分课程很容易成为一种无法消化的知识大杂烩。

• 不完全证明

　　不完全证明是过分证明与菜谱水平之间权衡这种的最好的办法。在合适的场合（趣味出版物，预备知识不足够理解完全证明的学生）应用不完全证明会很有用，但是他们的用处绝对不是去替代完全证明，这点它们永远也办不到。

　　举一个被高斯称为"代数基本定理"的命题：一个n 阶方程恰有n 个根。

　　因为它很有用，因此这个命题经常被提出来给那些预备知识不多尚不足以理解其完全证明的学生。可是这些学生们知道一阶方程有一个根，两阶方程有两个根。但是，这个困难的命题还有一个很容易证明的部分：没有任何n 阶方程会具有多于n 个的不同的根。（还是说细一点吧：假设它有多于 n个不同的根，把方程写成因式连乘的形式，最终它会变成一个大于n 阶的方程，因此假定不成立）。上述这些事实是否构成这基本定理的一个完全证明呢？绝不。但是他们足以使这个基本定理有趣、可信——并且使学生牢记这个基本定理，这是主要的。（这个例子有它的历史价值。大约250 年之久，数学家一直相信这个基本定理而并无完全证明——实际上没有上述更多的基础）

　　不完全证明的作用与趣味，在某种程度上可由我们所研究的解题过程加以说明。在解题中的某些经验表明：证明的最初念头经常是不完全的。

倒着干

试试找出这个数字游戏题的答案：有两个容器，小桶的容器容量是4 升，大桶的容量9 升，怎样才能从河中恰好打上6 升水来？

当碰到这个难题时，我们就象绝大多数人所做的那样。从两个空桶开始，试试这个，试试那个，我们倒空又装满。而当我们不成功时，我们重新开始，试试别的做法。我们在向前干，即，从给定的初始情况到所期望的最终情况，从已知数据到未知数。经过多次试验，我们偶尔也会成功。

但是有卓越才能的人，或者从数学课本中所学到的不仅仅是套公式演算的人，不会在这种实验里浪费太多的时间（注：不是不浪费时间，而是不在那儿一直浪费时间、碰概率，能在合适的时机从常规的思维模式中跳出来很重要呢：），而是回过头去开始倒着干。

可以这样来思考，想要取得6 升水，那么最终这6 升水肯定装在容量为9 升的打个大桶里，那么如何取这6 升水呢？把9 升水装满了倒掉3 升就可以了，可我没有3 升的容器啊，怎么倒掉3 升水呢？为了做到这点，小桶中必须恰好有一升水，这就是念头（完成这一步并非易事，很少人能毫不犹豫地想到它。事实上，认识到这一步的意义，我们就可预见到接下来求解的一个梗概）。如何使得小桶中恰好有一桶水呢？再进一步，它和大桶中恰好有一升水是等价的，那么问题又变换成了，如何使大桶中恰好有一升水呢？我们会发现，将大桶装满，倒出4 升水给小桶，把小桶里的水倒入河中，一共操作两次，我们就得到了一升水。问题到这里就解决了，只不过解决问题的过程和解答的过程两者次序是相反的。把下图所示的整个过程倒过来就是我们的答案。这个问题给我们的启示除了倒着干，还有不要拘泥于常规的思维框架中（以前整理了一个过桥谜题，在这儿），思考问题，首先进行常规思维，解决不了，在合适的时机就应当跳出框架来看看。

毫无疑问，这个方法有某些发人深思之处。不照直走一条通往目标的道路，而是从目标走开，转过头来倒着干，这一方法有某种心理障碍。当我们发现合适的操作步骤后，我们必须在心里按照相反的次序去进行。我们对于这种反顺序，有某种心理上的嫌恶，如果我们不是小心翼翼提出来的话，它可能阻止一个很能干的学生去了解这种方法。

既然谈到了心理，下面有个很好玩的心理实验：如下图，一个篱笆围成正方形的三边，而另一边是敞开的。

 

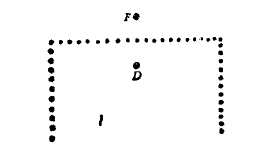
我们把一只狗放在D 上，而把食物放在F 上。对狗来说，它可能首先冲过去，好象要直接扑到食物上，但是，接着它便很快转过身来，匆忙地绕过篱笆，沿一条圆滑曲线毫不犹豫地跑到另一点F 上。然而，当点D 和F 相距甚近时，这狗要先花点时间向篱笆叫呀，抓呀，扑呀，然后才"想到"转过身去这一"好念头"。换上其他的动物，比如黑猩猩或者四岁儿童（对儿童来说把食物换成玩具更有吸引力），他们很容易就懂得绕过篱笆。而对于一只鸡来说，这个问题则惊人的困难。鸡会在靠近食物的篱笆那一边激动的转来转去，如果它终于走到了食物那里的话，也会在这之前浪费相当多的时间。在许多奔跑之后，它偶然可能会成功。看来灵长类动物在解决问题方面确实有着天然的优势吗：-

这个实验想要告诉我们的是：绕过障碍是我们在解决任何一类问题时常作的事，鸡的行为就象某些人在解题时钻入了牛角尖，试了又试，最后碰巧成而又未深究其原因。我们又像狗一样，首先试图向前干（刚开始的时候不停摆弄两个水桶）不成功后才冒出转过身倒着干的念头，这给人的印象是：它具有较高的洞察力。在转过身去、从目标走开、不盯住目标行动、不按照直接通往目的地的路线走，这方面确实存在某种困难。鸡的困难同我们的困难显然是可以类比的。

---

最后，总结一下——请看文首那张表，是不是颠覆了最初对它的认知和鄙视？

 

All Rights Reserved.
Author：姜鹄.
Copyright © xp_jiang. 
转载请标明出处：http://www.cnblogs.com/xpjiang/p/5399219.html
以上.

看到这里的，给你自己点个赞吧。其实，我自己都嫌长呢。