编程之美-第2章 数字之魅
2.1 求二进制数数中1的个数
2.2 不要被阶乘吓到
2.3 寻找发帖”水王”
这个问题就是寻找数组中总数超过一半的数.
现在有一个数组,已知一个数出现的次数超过了一半,请用O(n)的复杂度的算法找出这个数。
第1种方法:
创建一个hash_map,key为数组中的数,value为此数出现的次数。遍历一遍数组,用hash_map统计每个数出现的次数,并用两个值存储目前出现次数最多的数和对应出现的次数。
这样可以做到O(n)的时间复杂度和O(n)的空间复杂度,满足题目的要求。
但是没有利用“一个数出现的次数超过了一半”这个特点。也许算法还有提高的空间。
第2种方法(推荐):
使用两个变量A和B,其中A存储某个数组中的数,B用来计数。开始时将B初始化为0。
遍历数组,如果B=0,则令A等于当前数,令B等于1;如果当前数与A相同,则B=B+1;如果当前数与A不同,则令B=B-1。遍历结束时,A中的数就是要找的数。
这个算法的时间复杂度是O(n),空间复杂度为O(1)。
#if 0 /* * 2.3 */ int overHalf(int *a,int n){ int A,B; B=0; for(int i=0;i<n;i++){ if(B==0){ A=a[i]; B=1; } else { if(A==a[i]) B++; else B--; } } return A; } int main(){ int array[]= {1, 2, 3, 1, 4, 5, 1, 1, 3, 1, 2, 1, 1}; int sz=sizeof(array)/sizeof(array[0]); cout<<overHalf(array,sz)<<endl; } #endif
参考: http://www.cnblogs.com/dartagnan/archive/2011/09/29/2195949.html
2.4 1的数目问题
一种直接的方法是从1到N,对每一个数分别进行判断.
#if 0 /* * 2.4 */ int countof1(int N){ int icnt=0; int ifactor=1; int ihigh=0,ilow=0,icurr=0; while(N/ifactor!=0){ ilow=N-(N/ifactor)*ifactor; icurr=(N/ifactor)%10; ihigh=N/(ifactor*10); switch(icurr){ case 0: icnt+=ihigh*ifactor; break; case 1: icnt+=ihigh*ifactor+ilow+1; break; default: icnt+=(ihigh+1)*ifactor; break; } ifactor*=10; } return icnt; } int main(){ cout<<countof1(1111111110)<<endl; } #endif
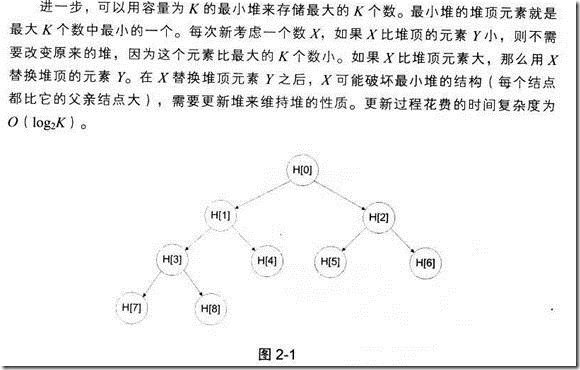
2.5 寻找最大的K个数
代码如下:
/* * 2.5 */ int partition(int *a,int low,int high){ int i=low,j=high+1; int pivot=a[low]; while(1){ do i++; while(a[i]<pivot); do j--; while(a[j]>pivot); if(i>=j) break; swap(a[i],a[j]); } swap(a[low],a[j]); return j; } int findK(int *a,int low,int high,int k){ if(low<high){ int mid=partition(a,low,high); int len=high-mid+1; if(len>k) return findK(a,mid+1,high,k); else if(len<k) return findK(a,low,mid-1,k-len); else return mid; } } void test_findk(){ const int N=8; const int K=4; int a[N] = {5 ,2 ,66 ,23, 11 ,1 ,4 ,55} ; int pos=findK(a , 0 , N - 1 , K) ; for(int i = 0 ; i < N ; i++) cout<<a[i]<<' ' ; cout<<endl; cout<<pos<<endl; } void adjust(int *b,int m,int n){ int j=m; int k=2*m; while(k<=n){ if(k<n&&b[k]>b[k+1]) k++; if(b[j]>b[k]) swap(b[j],b[k]); j=k; k*=2; } } void make_heap(int *a,int n){ int *b=a-1; for(int i=n/2;i>=1;i--) adjust(b,i,n); }
代码如下:
void findK2(int *a,int n,int k){ assert(k<n); int *b=new int[k]; int cnt=0; for(int i=0;i<n;i++){ if(cnt<k){ b[cnt++]=a[i]; } else{ make_heap(b,k); for(int j=0;j<k;j++) cout<<b[j]<<' '; cout<<endl; if(a[i]>b[0]) b[0]=a[i]; } } for(int i=0;i<k;i++) cout<<b[i]<<' '; cout<<endl; delete [] b; } void test_findk2(){ const int N=8; const int K=4; int a[N] = {5 ,2 ,66 ,23, 11 ,1 ,4 ,55} ; findK2(a,N,K); } int main(){ test_findk2(); }
2.6 精确表示浮点数
2.7 最大公约数问题
2.8 找出符合条件的整数
题目:任意给定一个正整数N,求一个最小的正整数M(M>1),使得N*M的十进制表示形式里只含有1和0.
解决这个问题首先考虑对于任意的N,是否这样的M一定存在。可以证明,M是一定存在的,而且不唯一。
简单证明:因为
这是一个无穷数列,但是数列中的每一项取值范围都在[0, N-1]之间。所以这个无穷数列中间必定存在循环节。即假设有s,t均是正整数,且s<t,有 。于是循环节长度为t-s。于是10^s = 10^t。因此有:
![]() ,所以
,所以
![]()
例如,取N=3,因为10的任何非负次方模3都为1,所以循环节周期为1.有:
给定N,求M的方法:
方法一:给定N,令M从2开始,枚举M的值直到遇到一个M使得N*M的十进制表示中只有1和0.
方法二:求出10的次方序列模N的余数序列并找出循环节。然后搜索这个余数序列,搜索的目的就是要在这个余数序列中找到一些数出来让它们的和是N的倍数。例如N=13,这个序列就是1,10,9,12,3,4然后不断循环。很明显有1+12=13,而1是10的0次方,12是10的3次方,所以这个数就是1000+1=1001,M就是1001/13=77。
方法三:因为N*M的取值就是1,10,11,100,101,110,111,......所以直接在这个空间搜索,这是对方法一的改进。搜索这个序列直到找到一个能被N整除的数,它就是N*M,然后可计算出M。例如N=3时,搜索树如下:
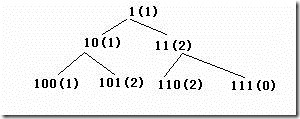
上图中括号内表示模3的余数。括号外表示被搜索的数。左子树表示0,右子树表示1.上图中搜索到第二层(根是第0层)时遇到111,它模3余数为0.所以N*M=111, M=111/3=37。
方法四:对方法三的改进。将方法三的搜索空间按模N余数分类,使得搜索时间和空间都由原来的指数级降到了O(N)。改进的原理:假设当前正在搜索由0,1组成的K位十进制数,这样的K位十进制数共有2^k个。假设其中有两个数X、Y,它们模N同余,那么在搜索由0、1组成的K+1位十进制数时,X和Y会被扩展出四个数:10X, 10X+1, 10Y, 10Y+1。因为X和Y同余(同余完全可以看作相等),所以10X与10Y同余,10X+1与10Y+1同余。也就是说由Y扩展出来的子树和由X扩展产生出来的子树产生完全相同的余数,如果X比Y小,那么Y肯定不是满足要求的最小的数,所以Y这棵子树可以被剪掉。这样,2^K个数按照模N余数分类,每类中只保留最小的那个数以供扩展。原来在这一层需要搜索2^K个数,现在只需要搜索O(N)个数。例如,当N=9时,第0层是1(1),
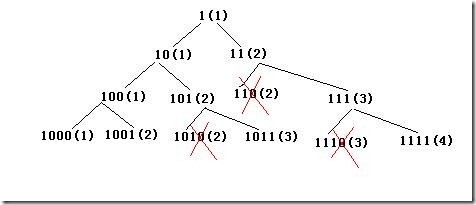
如上图所示,第2层的110,第三层的1010、1110都因为同一层有和它同余且更小的数而被剪掉。如果按照方法三搜索,第三层本来应该有8个结点,但现在只有4个结点。
代码如下:
#if 0 bool has_only_one_and_zero(unsigned int n){ while(n!=0){ if(n%10>=2) return false; n/=10; } return true; } void method1(int n){ int m; for(m=1;;m++){ if(has_only_one_and_zero(n*m)){ printf("n=%d,m=%d,n*m=%d\n",n,m,n*m); break; } } } void findNM(int N){ queue<int> Q; Q.push(1); while(!Q.empty()){ int t=Q.front(); Q.pop(); if(t%N==0){ printf("n=%d,m=%d,n*m=%d\n",N,t/N,t); break; } Q.push(t*10); Q.push(t*10+1); } } struct QNode{ int v,r; QNode(int value=0,int remain=0):v(value),r(remain){} }; void findNM2(int N){ queue<QNode> Q; Q.push(QNode(1,1)); while(!Q.empty()){ int sz=Q.size(); vector<bool> bn(N,false); while(sz--){ QNode t=Q.front(); Q.pop(); if(t.r==0){ printf("n=%d,m=%d,n*m=%d\n",N,t.v/N,t.v); return ; } if(!bn[t.r*10%N]){ bn[t.r*10%N]=true; Q.push(QNode(t.v*10,t.r*10%N)); } if(!bn[(t.r*10+1)%N]){ bn[(t.r*10+1)%N]=true; Q.push(QNode(t.v*10+1,(t.r*10+1)%N)); } } } } void test(){ int n; while(scanf("%d",&n)!=EOF){ method1(n); findNM(n); findNM2(n); } } int main(){ test(); } #endif
参考: http://www.cnblogs.com/bvbook/archive/2009/02/06/1385448.html
2.9 斐波那契数列问题
递推公式如下:
2.10 寻找数组中的最大值和最小值
试着用最小的比较次数去寻找数组中的最大值和最小值。
解法三,设置两个变量Max,Min。遍历数组,每两个数据进行比较,大的再跟Max比较,小的跟Min比较,共1.5N次。似乎是最少的比较次数了。
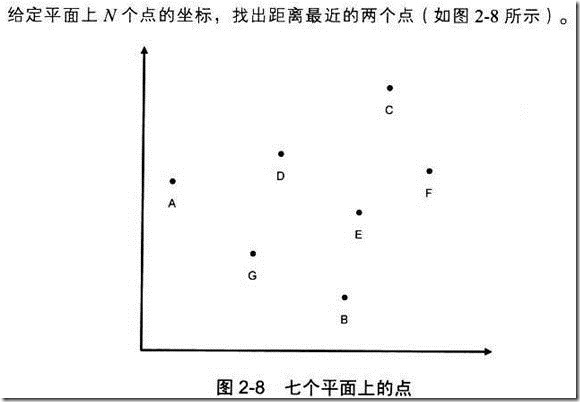
2.11 寻找最近点对
2.12 快速寻找满足条件的两个数
参考: http://www.cnblogs.com/justinzhang/archive/2012/04/25/2470405.html
2.13 子数组的最大乘积
两种方法的代码如下:
#if 0 int sub_array_max_multiply1(int *a,int n){ if(a==0||n<0) return -1; int *s=new int[n];//s[i]=s[i-1]*a[i-1]; int *t=new int[n];//t[j]=t[j+1]*a[j+1]; s[0]=1,t[n-1]=1; for(int i=1,j=n-2;i<n;i++,j--) s[i]=s[i-1]*a[i-1], t[j]=t[j+1]*a[j+1]; int p=0x80000000; int index=-1; for(int i=0;i<n;i++) if(p<s[i]*t[i])//s[i]*t[i]是除a[i]之外的其他元素的乘积 p=s[i]*t[i], index=i; cout<<p<<endl; delete [] s; delete [] t; return index; } int sub_array_max_multiply2(int *a,int n){ int zero_cnt=0,neg_cnt=0;//统计0和负数的个数 int neg_abs_min=0x7fffffff,//记录绝对值最小负数 neg_abs_max=0,//记录绝对值最大负数 pos_min=0x7fffffff;//记录最小正数 int zero_idx,neg_abs_min_idx, neg_abs_max_idx, pos_min_idx; for(int i=0;i<n;i++){ if(a[i]==0) zero_cnt++,zero_idx=i; else if(a[i]>0){ if(a[i]<pos_min) pos_min=a[i], pos_min_idx=i; } else{ neg_cnt++; int neg_abs=-a[i]; if(neg_abs<neg_abs_min) neg_abs_min=neg_abs, neg_abs_min_idx=i; else if(neg_abs>neg_abs_max) neg_abs_max=neg_abs, neg_abs_max_idx=i; } } if(zero_cnt>1){//0的个数多于1,所以N-1个元素的结果肯定是0 cout<<0<<endl; return zero_idx; } else if(zero_cnt==1){//只有一个0 if(neg_cnt%2==0)//如果负数个数为偶数,那么去除这个0之外的N-1个元素的乘积最大 return zero_idx;// else //负数个数为奇数个,那么用0替换任意一个数都可以,结果为0 return neg_abs_min_idx; } else {//不存在0 if(neg_cnt%2)//负数个数为奇数,去除绝对值最小的负数即可 return neg_abs_min_idx; else if(neg_cnt==n)//不存在正数情况,去除绝对值最大的负数 return neg_abs_max_idx; else//负数个数为偶数,去除最小正数 return pos_min_idx; } } int main(){ int arr[5] = {-2,-3,4,-1,6}; cout<<sub_array_max_multiply1(arr,5)<<endl; cout<<sub_array_max_multiply2(arr,5)<<endl; } #endif
2.14 求子数组之和的最大值
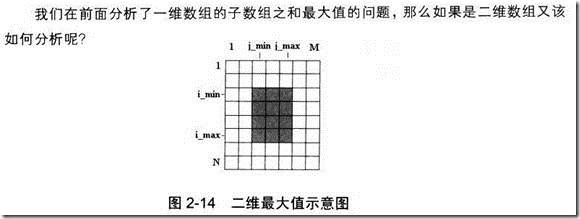
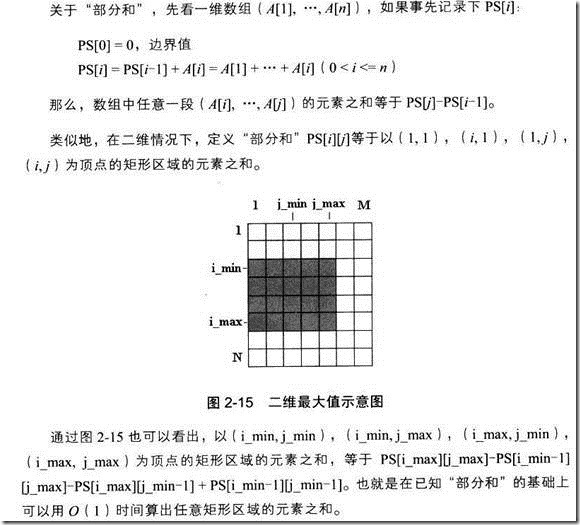
2.15 子数组之和的最大值(二维)
所以, 解法1就是遍历所有大小的矩形, 根据得到的部分和PS可以很容易计算矩形的内数字的和. 复杂度为O(M^2*N^2)
解法2是转化为一维的情况.
我们发现一维的解答可以线性完成,这里我们把问题从二维转化为一维以提高算法性能。
假设已经确定了矩阵区域的上下边界,不如知道矩阵区域的上下边界分布是第a行和第c行,接下来要确定左右边界。
我们把第a行和第c行之间的每一列看成一个整体,相当于一维数组中的一个元素(通过子矩阵部分和可以在O(1)时间内计算出整体之和)。
代码如下:
#if 0 /* * 2.15 */ //根据部分和矩阵PS计算出行范围[i1,i2],列范围[j1,j2]内的和 int matrix_sum(int **PS,int i1,int i2,int j1,int j2){ return PS[i2][j2]-PS[i1-1][j2]-PS[i2][j1-1]+PS[i1-1][j1-1]; } //打印出二维矩阵 void TMP(int **M,int row,int col){ for(int i=0;i<row;i++){ for(int j=0;j<col;j++) cout<<setw(3)<<M[i][j]; cout<<endl; } } //方法1:遍历所有的矩形进行求和 void matrix_max_sum(int **M,int row,int col){ int *Mem=new int[(row+1)*(col+1)]; int **PS=new int*[row+1]; for(int i=0;i<=row;i++) PS[i]=Mem+(col+1)*i; for(int i=0;i<=row;i++)//初始化第0列 PS[i][0]=0; for(int j=0;j<=col;j++)//初始化第0行 PS[0][j]=0; for(int i=1;i<=row;i++) for(int j=1;j<=col;j++) PS[i][j]=M[i][j]+PS[i-1][j]+PS[i][j-1]-PS[i-1][j-1];//计算部分和 TMP(PS,row+1,col+1); int c1=-1,c2=-1,r1=-1,r2=-1; int max_sum=0x80000000; for(int i1=1;i1<=row;i1++) for(int i2=i1;i2<=row;i2++) for(int j1=1;j1<=col;j1++) for(int j2=j1;j2<=col;j2++) { int tmp=matrix_sum(PS,i1,i2,j1,j2);//计算[i1,i2][j1,j2]范围内矩形,并判断是否为最大值 if(tmp>max_sum){ max_sum=tmp; r1=i1,r2=i2,c1=j1,c2=j2; } } cout<<'['<<r1<<' '<<r2<<' ' <<c1<<' '<<c2<<"]="<<max_sum<<endl; delete[] Mem; delete[] PS; } //方法2:转化为一维的情况 void matrix_max_sum2(int **M,int row,int col){ int *Mem=new int[(row+1)*(col+1)]; int **PS=new int*[row+1]; for(int i=0;i<=row;i++) PS[i]=Mem+(col+1)*i; for(int i=0;i<=row;i++) PS[i][0]=0; for(int j=0;j<=col;j++) PS[0][j]=0; for(int i=1;i<=row;i++) for(int j=1;j<=col;j++) PS[i][j]=M[i][j]+PS[i-1][j]+PS[i][j-1]-PS[i-1][j-1]; TMP(PS,row+1,col+1); int c1=-1,c2=-1,r1=-1,r2=-1; int max_sum=0x80000000; for(int a=1;a<=row;a++) for(int c=a;c<=row;c++){ // 将子矩阵上下边界设为第a行和第c行,在这些子矩阵中取最大值 int tail=matrix_sum(PS,a,c,1,1); // cout<<"tail="<<tail<<' '; int c1_t=1;//记录最大和的起始位置 for(int j=2;j<=col;j++){ int tmp=matrix_sum(PS,a,c,j,j); if(tail<0) tail=tmp,c1_t=j; else tail+=tmp; // cout<<tail<<"<c1="<<c1<<"> "; if(tail>max_sum) max_sum=tail,r1=a,r2=c,c1=c1_t,c2=j; } // cout<<endl; } cout<<'['<<r1<<' '<<r2<<' ' <<c1<<' '<<c2<<"]="<<max_sum<<endl; delete[] Mem; delete[] PS; } int main(){ const int row=4,col=4; int B[][col]={0,-2,-7,0, 9,2,-6,2, -4,1,-4,1, -1,8,0,-2 }; int *tmp[]={0,(int*)(*B-1),(int*)(*(B+1)-1),(int*)(*(B+2)-1),(int*)(*(B+3)-1)}; // TMP(tmp,row,col); matrix_max_sum(tmp,row,col); matrix_max_sum2(tmp,row,col); } #endif
对于问题1:
代码如下:
#include <iostream> #include <algorithm> using namespace std; #define MAXN 1003 int A[MAXN][MAXN]; long long PS[MAXN][MAXN]; inline long long MatrixSum(int s, int t, int i, int j) { return PS[i][j]-PS[i][t-1]-PS[s-1][j]+PS[s-1][t-1]; } int main() { int m, n, i, j; cin >> n >> m; for (i=1; i<=n; i++) for (j=1; j<=m; j++) cin >> A[i][j]; for (i=0; i<=n; i++) PS[i][0] = 0; for (j=0; j<=m; j++) PS[0][j] = 0; // 计算矩阵的部分和 for (i=1; i<=n; i++) for (j=1; j<=m; j++) PS[i][j] = A[i][j]+PS[i-1][j]+PS[i][j-1]-PS[i-1][j-1]; int a, c; long long All = A[1][1]; // 上下边界不会跨过第n行和第1行 for (a=1; a<=n; a++) for (c=a; c<=n; c++) { // 将子矩阵上下边界设为第a行和第c行 // 左右边界不会跨过第m列和第1列 long long Tail = MatrixSum(a, 1, c, 1); for (j=2; j<=m; j++) { Tail = max(MatrixSum(a, j, c, j), MatrixSum(a, j, c, j)+Tail); All = max(Tail, All); } // 左右边界会跨过第n列和第1列 long long Sum = MatrixSum(a, 1, c, 1); long long Start = Sum; int sind = 1; for (i=2; i<=m; i++) { Sum += MatrixSum(a, i, c, i); if (Sum > Start) {Start = Sum; sind = i;} } Tail = MatrixSum(a, m, c, m); int tind = m; for (j=m-1; j>=1; j--) { Sum += MatrixSum(a, j, c, j); if (Sum > Tail) {Tail = Sum; tind = j;} } if (sind<tind && Start+Tail>All) All = Start+Tail; } cout << All; }
对于问题3:
思路和二维一样,但时间复杂度增加到O(n^5)。通过将高维转化为低维的方法,每增加一维时间复杂度要增加O(n^2)。
方体的部分和计算公式如下:PS[i][j][k] = A[i][j][k]+PS[i-1][j][k]+PS[i][j-1][k]+PS[i][j][k-1]-PS[i-1][j-1][k]-PS[i-1][j][k-1]-PS[i][j-1][k-1]+PS[i-1][j-1][k-1];
代码如下:
#include <iostream> #include <algorithm> using namespace std; #define MAXN 1003 int A[MAXN][MAXN][MAXN]; int PS[MAXN][MAXN][MAXN]; inline int CubeSum(int a, int b, int c, int d, int i, int j) { return PS[b][d][j]-PS[a-1][d][j]-PS[b][c-1][j]-PS[b][d][i-1]+ PS[a-1][c-1][j]+PS[a-1][d][i-1]+PS[b][c-1][i-1]-PS[a-1][c-1][i-1]; } int main() { int n, m, h, i, j, k; cin >> n >> m >> h; for (i=1; i<=n; i++) for (j=1; j<=m; j++) for (k=1; k<=h; k++) cin >> A[i][j][k]; for (i=0; i<=n; i++) for (j=0; j<=m; j++) PS[i][j][0] = 0; for (i=0; i<=n; i++) for (k=0; k<=h; k++) PS[i][0][k] = 0; for (j=0; j<=m ; j++) for (k=0; k<=h; k++) PS[0][j][k] = 0; // 计算长方体的部分和 for (i=1; i<=n; i++) for (j=1; j<=m; j++) for (k=1; k<=h; k++) PS[i][j][k] = A[i][j][k]+PS[i-1][j][k]+PS[i][j-1][k]+PS[i][j][k-1]- PS[i-1][j-1][k]-PS[i-1][j][k-1]-PS[i][j-1][k-1]+PS[i-1][j-1][k-1]; int a, b, c, d; int All = A[1][1][1]; // 限制第一维的取值范围 for (a=1; a<=n; a++) for (b=a; b<=n; b++) // 限制第二维的取值范围 for (c=1; c<=m; c++) for (d=c; d<=m; d++) { // 只剩下最后一维没有确定,利用一维部分和的方法 int Tail = CubeSum(a,b,c,d,1,1); for (j=2; j<=k; j++) { int cur = CubeSum(a,b,c,d,j,j); Tail = max(Tail+cur, cur); All = max(Tail, All); } } cout << All; }
参考: http://blog.csdn.net/linyunzju/article/details/7723730
2.16 数组中的最长递增子序列
解法1:
2.17 数组循环移位
2.18 数组分割
问题:
1. 有一个无序、元素个数为2n的正整数数组,要求:如何能把这个数组分割为两个子数组,子数组的元素个数不限,并使两个子数组之和最接近。
2. 有一个无序、元素个数为2n的正整数数组,要求:如何能把这个数组分割为元素个数为n的两个数组,并使两个子数组之和最接近。
1. 解法1:
由于对两个子数组和最接近的判断不太直观,我们需要对题目进行适当转化。我们知道当一个子数组之和最接近原数组之和sum的一半时,两个子数组之和是最接近的。所以转化后的题目是:从2n个数中选出任意个数,其和尽量接近于给定值sum/2。
这个问题存储的是从前k个数中选取任意个数,且其和为s的取法是否存在dp[k][s]。之所以将选出的数之和放在下标中,而不是作为dp[k]的值,是因为那种做法不满足动态规划的前提——最优化原理,假设我们找到最优解有k个数p1p2...pk(选出的这k个数之和是最接近sum/2的),但最优解的前k-1个数p1p2...pk-1之和可能并不是最接近sum/2的,也就是说可能在访问到pk之前有另一组数q1q2....qk-1其和相比p1p2...pk-1之和会更接近sum/2,即最优解的子问题并不是最优的,所以不满足最优化原理。因此我们需要将dp[k]的值作为下标存储起来,将这个最优问题转化为判定问题,用带动态规划的思想的递推法来解。
外阶段:在前k1个数中进行选择,k1=1,2...2*n。
内阶段:从这k1个数中任意选出k2个数,k2=1,2...k1。
状态:这k2个数的和为s,s=1,2...sum/2。
决策:决定这k2个数的和有两种决策,一个是这k2个数中包含第k1个数,另一个是不包含第k1个数。
dp[k][s]表示从前k个数中取任意个数,且这些数之和为s的取法是否存在。
#include <iostream> #include <algorithm> using namespace std; #define MAXN 101 #define MAXSUM 100000 int A[MAXN]; bool dp[MAXN][MAXSUM]; // dp[k][s]表示从前k个数中去任意个数,且这些数之和为s的取法是否存在 int main() { int n, i, k1, k2, s, u; cin >> n; for (i=1; i<=2*n; i++) cin >> A[i]; int sum = 0; for (i=1; i<=2*n; i++) sum += A[i]; memset(dp,0,sizeof(dp)); dp[0][0]=true; // 外阶段k1表示第k1个数,内阶段k2表示选取数的个数 for (k1=1; k1<=2*n; k1++) // 外阶段k1 { for (k2=k1; k2>=1; k2--) // 内阶段k2 for (s=1; s<=sum/2; s++) // 状态s { //dp[k1][s] = dp[k1-1][s]; // 有两个决策包含或不包含元素k1 if (s>=A[k1] && dp[k2-1][s-A[k1]]) dp[k2][s] = true; } } // 之前的dp[k][s]表示从前k个数中取任意k个数,经过下面的步骤后 // 即表示从前k个数中取任意个数 for (k1=2; k1<=2*n; k1++) for (s=1; s<=sum/2; s++) if (dp[k1-1][s]) dp[k1][s]=true; // 确定最接近的给定值sum/2的和 for (s=sum/2; s>=1 && !dp[2*n][s]; s--); printf("the differece between two sub array is %d\n", sum-2*s); }
解法2:
由于题目不限制子数组的元素个数,限制条件少,可以进行优化。实际上解法1的思路主要是为了题目2做铺垫,使得题目2的解法不至于太难理解。该题实际上有更简单的解法,该解法的思路和0-1背包问题的思路是一样的。
#include <iostream> using namespace std; #define MAXN 101 #define MAXSUM 100000 int A[MAXN]; bool dp[MAXN][MAXSUM]; // dp[k][s]表示从前k个数中取任意个数,且这些数之和为s的取法是否存在 int main() { int k, s, u, i, n; cin >> n; for (i=1; i<=2*n; ++i) cin >> A[i]; int sum = 0; for (i=1; i<=2*n; ++i) sum += A[i]; dp[0][0] = true; // 阶段k表示第k个数 for (k=1; k<=2*n; ++k) // 注意状态可取0 for (s=0; s<=(sum>>1); ++s) { // 加上第k个数,或不加它所能得到的和 if (s>=A[k]) dp[k][s] = dp[k-1][s-A[k]] || dp[k-1][s]; else dp[k][s] = dp[k-1][s]; } for (s=(sum>>1); s>=1 && !dp[2*n][s]; --s); cout << sum-2*s; }
2. 解法:
但本题还增加了一个限制条件,即选出的物体数必须为n,这个条件限制了内阶段k2的取值范围,并且dp[k][s]的含义也发生变化。这里的dp[k][s]表示从前k个数中取k个数,且k不超过n,且这些数之和为s的取法是否存在。
#include <iostream> #include <algorithm> using namespace std; #define MAXN 101 #define MAXSUM 100000 int A[MAXN]; bool dp[MAXN][MAXSUM]; // 题目可转换为从2n个数中选出n个数,其和尽量接近于给定值sum/2 int main() { int n, i, k1, k2, s, u; cin >> n; for (i=1; i<=2*n; i++) cin >> A[i]; int sum = 0; for (i=1; i<=2*n; i++) sum += A[i]; memset(dp,0,sizeof(dp)); dp[0][0]=true; // 对于dp[k][s]要进行u次决策,由于阶段k的选择受到决策的限制, // 这里决策选择不允许重复,但阶段可以重复,比较特别 for (k1=1; k1<=2*n; k1++) // 外阶段k1 for (k2=min(k1,n); k2>=1; k2--) // 内阶段k2 for (s=1; s<=sum/2; s++) // 状态s // 有两个决策包含或不包含元素k1 if (s>=A[k1] && dp[k2-1][s-A[k1]]) dp[k2][s] = true; // 确定最接近的给定值sum/2的和 for (s=sum/2; s>=1 && !dp[n][s]; s--); printf("the differece between two sub array is %d\n", sum-2*s); }
参考: http://blog.csdn.net/linyunzju/article/details/7729774
2.19 区间重合判断
问题:
1. 给定一个源区间[x,y]和N个无序的目标区间[x1,y1] [x2,y2] ... [xn,yn],判断源区间[x,y]是不是在目标区间内。
2. 给定一个窗口区域和系统界面上的N个窗口,判断这个窗口区域是否被已有的窗口覆盖。
1. 解法:
先用区间的左边界值对目标区间进行排序O(nlogn),对排好序的区间进行合并O(n),对每次待查找的源区间,用二分查出其左右两边界点分别处于合并后的哪个源区间中O(logn),若属于同一个源区间则说明其在目标区间中,否则就说明不在。
#include <algorithm> using namespace std; struct Line { int low, high; bool operator<(const Line &l) const {return low<l.low;} }; #define MAXN 10001 Line lines[MAXN]; // 目标区间 int ncnt = 0; // 合并后区间的个数 #define N 101 Line sl[N]; // 待查询的源区间 // 用二分查找找出key所在的区间,以区间的low作为划分 int GetIndex(int key) { int u, v; u = 0; v = ncnt-1; while (u<=v) // u,v可取等号 { int m = (u+v)>>1; if (key >= lines[m].low) u = m+1; else v = m-1; } return v; } int main() { int n, k, i, j; cin >> n >> k; // n是目标区间的个数,k是待查询的源区间的个数 for (i=0; i<n; i++) cin >> lines[i].low >> lines[i].high; for (i=0; i<k; i++) cin >> sl[i].low >> sl[i].high; // 排序O(nlogn) sort(lines, lines+n); // 合并O(n) int lasthigh = lines[0].high; for (i=1; i<n; i++) if (lasthigh >= lines[i].low) lasthigh = lines[i].high; else { lines[ncnt++].high = lasthigh; lines[ncnt].low = lines[i].low; lasthigh = lines[i].high; } lines[ncnt++].high = lasthigh; for (i=0; i<k; i++) { // 单词查找时间O(logn) int s1 = GetIndex(sl[i].low); int s2 = GetIndex(sl[i].high); if (s1==s2 && sl[i].high <= lines[s2].high) printf("Yes\n"); else printf("No\n"); } }
2. 解法:
这个问题适合使用线段树来解答,单次查找的时间复杂度为O(nlogn),当然也能用数组解答,但单次查找的时间复杂度会增加到O(n^2)。这里我们直接使用线段树来解答。
线段树是一棵二叉树,将数轴划分成一系列的初等区间[I, I+1] (I=1,2,..,N-1)。每个初等区间对应于线段树的一个叶结点。线段树的内部结点对应于形如[ I, J ](J – I > 1)的一般区间。由于线段树给每一个区间都分配了结点,利用线段树可以求区间并后的总长度与区间并后的线段数。先给出测试数据(前4行是系统界面上已有的N个窗口,之后的一行是待测试的窗口区域),后面是代码:
4
-15 0 5 10
-5 8 20 25
15 -4 24 14
0 -6 16 4
2 15 10 22
#include <iostream> #include <cmath> #include <algorithm> using namespace std; // 线段树的结点 struct SegNode { int low, high; // 线段的两端点索引 int ncover; // 线段被覆盖的次数 SegNode *left; // 结点的左子树 SegNode *right; // 结点的右子树 SegNode() {low=high=0;ncover=0; left=right=NULL;} }; // 构造线段树,它是一个完全二叉树 void BuildSegTree(SegNode *&tree, int *index, int low, int high) { if (low < high) { tree = new SegNode; tree->low = low; tree->high = high; if (high-low>1) { int m = (low+high)/2; BuildSegTree(tree->left, index, low, m); BuildSegTree(tree->right, index, m, high); } } } // 往线段树中插入线段,即用线段(low,high)来覆盖线段树 void InsertSegTree(SegNode *tree, int low, int high) { // 先序遍历 if (low<=tree->low && tree->high<=high) tree->ncover++; else if (tree->high-tree->low > 1) { int m = (tree->low+tree->high)/2; if (low < m) InsertSegTree(tree->left, low, high); if (m < high) InsertSegTree(tree->right, low, high); } } // 从线段树中删除线段 void DeleteSegTree(SegNode *tree, int low, int high) { if (low<=tree->low && tree->high<=high) tree->ncover--; else if (tree->high-tree->low > 1) { int m = (tree->low+tree->high)/2; if (low < m) DeleteSegTree(tree->left, low, high); if (m < high) DeleteSegTree(tree->right, low, high); } } // 线段树中是否包含线段(low,high) bool FindSegTree(SegNode *tree, int low, int high) { // 若当前区间被覆盖,且线段(low,high)属于当前区间则返回覆盖 if (tree->ncover && tree->low <= low && high <= tree->high ) return true; // 若(low,high)没被当前区间覆盖,则将其分为两段, // 分别考虑是否被子结点表示的区间覆盖 else if (tree->high - tree->low > 1) { int m = (tree->low + tree->high) >> 1; bool ret = true; if (low<m) ret = FindSegTree(tree->left, low, high<m?high:m); if (!ret) return false; if (m<high) ret = FindSegTree(tree->right, m<low?low:m, high); if (!ret) return false; return true; } return false; } #define LEFT true #define RIGHT false #define INF 10000 // 表示竖直方向的线段 struct Line { int starty, endy; // 竖线的长度 int x; // 竖线的位置 bool inout; // 竖线是长方形的左边还是右边 bool operator<(const Line& a) const{ // 依据x坐标进行排序 return x<a.x; } }; // 所有竖直方向的线段 Line lines[INF]; // 对横向超元线段进行分组 int index[INF]; int nCnt = 0; // 获取key的位置 int GetIndex(int key) { // 用二分查找查出key在index中的位置 return lower_bound(index,index+nCnt,key)-index; } // 获取key的位置或比它小的最大数的位置 int GetLower(int key) { size_t pos = lower_bound(index,index+nCnt,key)-index; if (key == index[pos]) return pos; else return pos-1; } // 获取key的位置或比它大的最小数的位置 int GetUpper(int key) { return lower_bound(index,index+nCnt,key)-index; } int main() { int nRec; cin >> nRec; int i, j; int x[2], y[2]; // 读取nRec个窗口的数据 for (i=0; i<nRec; i++) { cin >> x[0] >> y[0] >> x[1] >> y[1]; // 记录每个长方形的两条竖直边 lines[2*i].x=x[0]; lines[2*i+1].x=x[1]; lines[2*i].starty=lines[2*i+1].starty=min(y[0],y[1]); lines[2*i].endy=lines[2*i+1].endy=max(y[0],y[1]); lines[2*i].inout=LEFT; lines[2*i+1].inout=RIGHT; // 对竖直的线段进行离散化 index[2*i]=y[0]; index[2*i+1]=y[1]; } // 待查询的窗口区域 Line search[2]; cin >> x[0] >> y[0] >> x[1] >> y[1]; search[0].x=x[0]; search[1].x=x[1]; search[0].starty=search[1].starty=min(y[0],y[1]); search[0].endy=search[1].endy=max(y[0],y[1]); search[0].inout=LEFT; search[1].inout=RIGHT; // 对x坐标进行排序O(nlogn) sort(index, index+2*nRec); sort(lines, lines+2*nRec); // 排除index数组中的重复数据O(n) for (i=1; i<2*nRec; i++) if (index[i]!=index[i-1]) index[nCnt++] = index[i-1]; index[nCnt++] = index[2*nRec-1]; // 建立线段树 SegNode *tree; BuildSegTree(tree, index, 0, nCnt-1); // 单词查找的时间复杂度为O(nlogn) bool res; InsertSegTree(tree, GetIndex(lines[0].starty), GetIndex(lines[0].endy)); for (i=1; i<2*nRec; i++) { if (lines[i].inout==LEFT) // 遇窗口的左边界,将其加入线段树 InsertSegTree(tree, GetIndex(lines[i].starty), GetIndex(lines[i].endy)); else // 遇窗口的右边界,将其删出线段树 DeleteSegTree(tree, GetIndex(lines[i].starty), GetIndex(lines[i].endy)); if (lines[i].x!=lines[i-1].x && search[0].x < lines[i+1].x && search[1].x > lines[i].x) { // 从待查窗口区域的左边界开始查询直到其右边界结束查询 res = FindSegTree(tree, GetLower(search[0].starty), GetUpper(search[0].endy)); if (!res) break; }else if (search[1].x <= lines[i].x) break; } if (res) printf("Yes\n"); else printf("No\n"); return 0; }
参考: http://blog.csdn.net/linyunzju/article/details/7737060
2.21 只考加法的面试题







































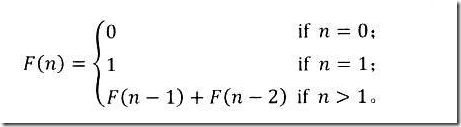






















































 浙公网安备 33010602011771号
浙公网安备 33010602011771号