slam十四讲(四)相机的运动
相机模型
-
针孔相机模型

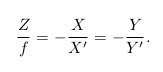
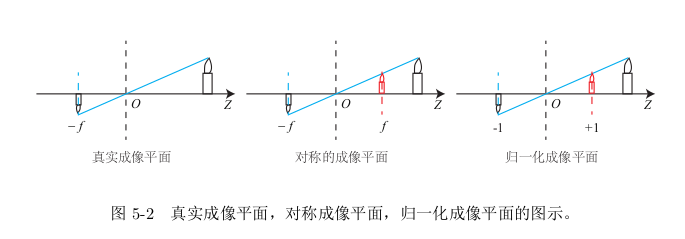
在相机中,我们最终获得的是一个个的像素,这需要在成像平面上对像进行采样和量化。为了描述传感器将感受到的光线转换成图像像素的过程,我们设在物理成像平面上固定着一个像素平面 o − u − v。我们在像素平面得到了 P ′ 的像素坐标:[u, v] T 。
像素坐标系 ¬ 通常的定义方式是:原点 o ′ 位于图像的左上角,u 轴向右与 x 轴平行,v轴向下与 y 轴平行。像素坐标系与成像平面之间,相差了一个缩放和一个原点的平移。我们设像素坐标在 u 轴上缩放了 α 倍,在 v 上缩放了 β 倍。同时,原点平移了 [c x , c y ] T 。那么,P ′ 的坐标与像素坐标 [u, v] T 的关系为: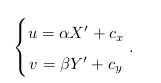
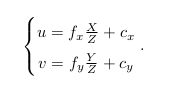
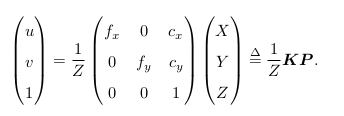
该式中,我们把中间的量组成的矩阵称为相机的内参数矩阵(Camera Intrinsics)K
我们使用的是 P 在相机坐标系下的坐标。由于相机在运动,所以 P 的相机坐标应该是它的世界坐标(记为 P w ),
根据相机的当前位姿,变换到相机坐标系下的结果。
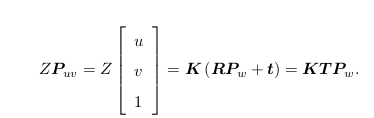
相机的位姿 R, t 又称为相机的外参数(Camera Extrinsics)。相比于不变的内参,外参会随着相机运动发生改变,同时也是 SLAM中待估计的目标,代表着机器人的轨迹。
可以简单地把 Z 去掉:
Puv = KTPw .
对于这个三维向量,我们还可以按照齐次坐标的方式,把最后一维进行归一化处理,得到了 P 在相机归一化平面上的投影: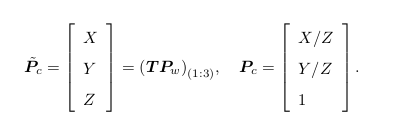
这时 P c 可以看成一个二维的齐次坐标,称为归一化坐标。它位于相机前方 z = 1 处的平面上。该平面称为归一化平面。
-
畸变
由透镜形状引起的畸变称之为径向畸变。
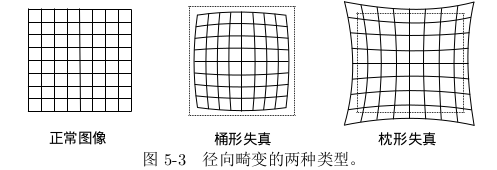
我们可以用一个多项式函数来描述畸变前后的坐标变化:这类畸变可以用和距中
心距离有关的二次及高次多项式函数进行纠正:
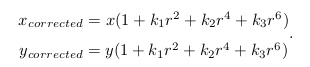



 浙公网安备 33010602011771号
浙公网安备 33010602011771号