平面最近点对

问题

题目描述

给定平面上 n 个点，找出其中的一对点的距离，使得在这 n 个点的所有点对中，该距离为所有点对中最小的。

输入格式

第一行一个整数 n，表示点的个数，n 不超过 10001。
接下来 n 行，每行两个实数 x,y，表示一个点的行坐标和列坐标。

输出格式

仅一行，一个实数，表示最短距离，四舍五入保留 4 位小数。、

数据规模

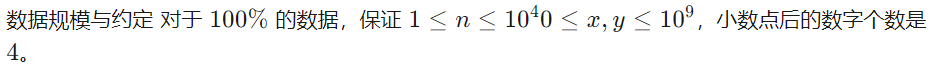
输入样例

3
1 1
1 2
2 2

10
1 1
2 3
4 5
7 6
5 6
8 3
4 7
6 4
9 5
4 3

9
1 1
2 3
4 5
7 6
5 6
8 3
4 7
6 6
9 5

输出样例

1.0000

1.4142

1.0000

思考

下次一定

代码

点击查看代码

#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
#include <stdio.h>
using namespace std;
vector<pair<int, int>> p;
int temp[10001];
bool comp(const pair<int, int> a, const pair<int, int> b)
{
    if (a.first < b.first)
        return true;
    else if (a.first > b.first)
        return false;
    else
    {
        if (a.second <= b.second)
            return true;
        else if (a.second > b.second)
            return false;
    }
}
bool cmps(const int a, const int b)
{
    return p[a].second < p[b].second;
}
double get_dis(int a, int b)
{
    return sqrt((p[a].first - p[b].first) * (p[a].first - p[b].first) + (p[a].second - p[b].second) * (p[a].second - p[b].second));
}
double divide(int l, int r)
{
    if (l == r)
        return 0x3f3f3f3f;
    else if (l + 1 == r)
        return get_dis(l, r);

    else
    {
        int mid = (l + r) / 2;

        double d1 = divide(l, mid);

        double d2 = divide(mid + 1, r);

        double d = min(d1, d2);
        int midx = p[mid].first; //中位线

        int k = 0;
        for (int i = l; i < r; i++)
            if (fabs(p[i].first - p[mid].first) <= d)
                temp[k++] = i;
        sort(temp, temp + k, cmps);
        for (int i = 0; i < k; i++)
            for (int j = i + 1; j < k && p[temp[j]].second - p[temp[i]].second < d; j++)
                d = min(d, get_dis(temp[i], temp[j]));

        return d;
    }
}
int main()
{
    int n, x, y;
    cin >> n;
    for (int i = 0; i < n; i++)
    {
        cin >> x >> y;
        p.push_back(make_pair(x, y));
    }
    sort(p.begin(), p.end(), comp);

    printf("%.4f\n", divide(0, p.size() - 1));
    return 0;
}