Let's play a game

问题

题目描述

输入描述

样例描述

第一行一个整数，为最少操作次数。

样例输入

5 2
1 2 4 2 5

2

---

5 2
1 2 2 2 2

4

样例解释

数据规模与约定

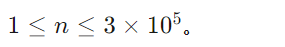
思考

参考博客

贪心法

从左向右扫描要删除的数到左侧最近的2的某次幂的距离

1.如果要删除的数直接在2的某次幂上，那么直接删除，操作次数加1即可；
2.如果要操作的数不在2的某次幂上，那么观察一下我们已经操作的次数，

如果我们操作的次数不小于（>=）该数到离其左侧最近的2的某次幂的距离，那么说明我们其实可以直接删除这个数了（因为我们之前的操作同样会引起后面的数向前移动），操作次数加1即可。

如果我们操作的次数小于该数到离其左侧最近的2的某次幂的距离，那么说明我们之前操作次数导致后面数向前移的次数还不够，（然后后面就体现了贪心思想，但是我可能表述的还不够清楚），此时，我们直接把我们的操作次数修改为该数到离其左侧最近的2的某次幂的距离+1为什么要这么写呢？为什么不是一个加法的形式呢(ans=ans+?),因为修改后的操作次数其实已经覆盖了删除其前面哪些数所需要的操作次数。

---

此外，这里还有一个值得学习的地方，就是如何快速求一个数离其左侧最近的2的某次幂的距离，利用了&运算的性质。

我们知道一个数x,如果x&(x-1)=0，那么这个数就是2的幂，不知道可以看这个,否则x&(x-1)的结果就是在x左侧的最大偶数（这个偶数一定比x小），将这个数记作y，之后我们继续y&(y-1)，一直到这个&运算的结果为0为止。这个思路是基于2的某次幂一定是个偶数，然后这个x&(x-1)一直从大到小找离x最近的偶数，找到之后两个数相减即可得到距离。

呃呃，这个方法思路写完了，发现并没有复杂度简单多少，也没有变快，甚至可能更慢。当时写这个方法的时候还没意识到这些，只知道这么做可以。不过，这个好歹是我自己想出来的，属于灵光一闪，还是非常值得庆祝的，之后还是直接借助pow(2,x)去判断好了。

代码

点击查看代码

#include <iostream>
#include <vector>
using namespace std;

int get_dis(int k)
{
    if (!(k & (k - 1)))
        return 0;
    else
    {
        int temp = k & (k - 1);
        int t;
        while (temp != 0)
        {
            t = temp;
            temp = t & (t - 1);
        }
        return k - t;
    }
}

int main()
{
    int n, k;
    vector<int> m;
    while (cin >> n >> k)
    {
        int key;
        for (int i = 1; i <= n; i++)
        {
            cin >> key;
            if (key == k)
            {
                m.push_back(get_dis(i));
            }
        }
        int ans = 0;
        for (int i = 0; i < m.size(); i++)
        {
            if (ans >= m[i])
                ans += 1;
            else
                ans = m[i] + 1;
        }
        cout << ans << endl;
    }

    return 0;
}