欧拉路径
https://www.acwing.com/problem/content/1621/
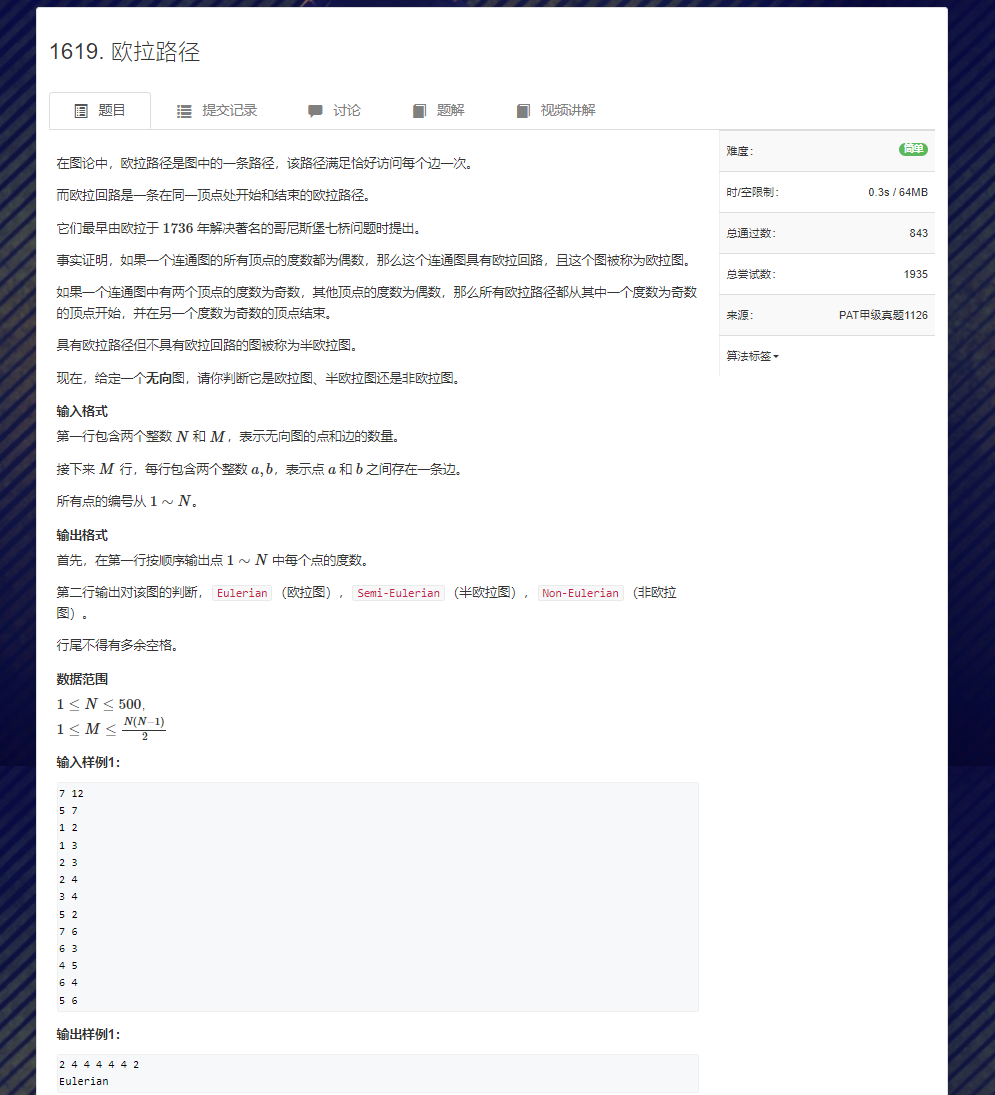
//欧拉图:连通 && 所有点的度数为偶
//半欧拉图:连通 && 只有2个点的度数为奇 其余度数为偶
//非欧拉图:else
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=550;
bool g[N][N],st[N];
int d[N]; //degrees 度数
int n,m;
int dfs(int u) //求联通点的数量
{
st[u]=1;
int cnt=1;
for(int i=1;i<=n;i++) if(!st[i]&&g[u][i]) cnt+=dfs(i);
return cnt;
}
int main()
{
cin>>n>>m;
while(m--)
{
int a,b;
cin>>a>>b;
g[a][b]=g[b][a]=true;
d[a]++,d[b]++;
}
int cnt=dfs(1);
cout<<d[1]<<" ";
for(int i=2;i<=n;i++)cout<<d[i]<<" ";
cout<<endl;
if(cnt==n)
{
int s=0;
for(int i=1;i<=n;i++)
if(d[i]%2)s++;
if(s==0)cout<<"Eulerian";
else if(s==2)cout<<"Semi-Eulerian";
else cout<<"Non-Eulerian";
}
else cout<<"Non-Eulerian";
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号