算法竞赛进阶指南 0x69 二分图的覆盖与独立集

最小点覆盖

在一个图中，求一个点的数目最少的一个点集，使得每一条边的两个端点中至少有一个属于这个集合。

由于任意图的最小点覆盖存在一些难度，所以这里只讨论二分图的最小点覆盖。

二分图的最小（点）覆盖的点的个数等于最大匹配的边的个数。

其中这些点的取法为：

1. 对这一个图进行一次匈牙利算法，求出最大匹配。
2. 在左部中，找到所有没有匹配的点，开始遍历。在同时标记访问过以及没有访问过的点。
3. 最小覆盖中的点的取法就是左部的没有遍历的点，加上右边的访问过的点。

证明

一、证明：最小覆盖要求的点的数量比最大匹配的边数多或者相等

不妨设最大匹配的边数是M

最大匹配中的边是原来的图中边集的子集合，由于最大匹配有一个性质：没有两条边交于一个定点，所以要想覆盖最大匹配中的所有的边，就需要M个点，而对于原来的图，就需要大于等于M个点。

二、构造出来一种 最小覆盖要求的点的数量等于最大匹配的边数的情况。

根据上方所确定的取法，现在进行证明可行性。

• 这样取的点保证覆盖所有的点
  对于匹配边，如果右部被访问过，那么左部也一定会被访问（回溯）。所以对于匹配边的两个端点，要么同时为访问过的，要么同时为未访问过的，而现在取左侧的未访问点，右侧的访问点，这样，就完全覆盖了匹配边。
  对于非匹配边，没有覆盖的情况仅仅是左侧 访问过，右侧 没有访问 过。这类情况就会导致出现交错路，而在之前已经求得了最大匹配，所以不会再有新的交错路产生。
• 证明所取得的点的数目等于最大匹配的边的数目
  左边的没有被访问的点一定是匹配点（从非匹配点出发dfs，肯定非匹配点全部被访问），右边访问过的点一定是匹配点（否则就会产生交错路）。所以左右两边所取的点全部都是匹配点，因为一个匹配边所连接的两个端点要么同时被访问，要么同时没有被访问，并且选的是 左部的没有访问的点，加上右边的访问过的点。所以一个匹配边所连接的两个端点中的一个会被计数。所以最小点覆盖等于最大匹配的边数。

AcWing376. 机器任务

有两台机器 A，B 以及 K 个任务。

机器 A 有 N 种不同的模式（模式 0∼N−1），机器 B 有 M 种不同的模式（模式 0∼M−1）。

两台机器最开始都处于模式 0。

每个任务既可以在 A 上执行，也可以在 B 上执行。

对于每个任务 i，给定两个整数 a[i] 和 b[i]，表示如果该任务在 A 上执行，需要设置模式为 a[i]，如果在 B 上执行，需要模式为 b[i]。

任务可以以任意顺序被执行，但每台机器转换一次模式就要重启一次。

求怎样分配任务并合理安排顺序，能使机器重启次数最少。

输入格式

输入包含多组测试数据。

每组数据第一行包含三个整数 N,M,K。

接下来 K 行，每行三个整数 i,a[i] 和 b[i]，i 为任务编号，从 0 开始。

当输入一行为 0 时，表示输入终止。

输出格式

每组数据输出一个整数，表示所需的机器最少重启次数，每个结果占一行。

数据范围

N,M<100,K<1000

0≤a[i]<N

0≤b[i]<M

输入样例：

5 5 10
0 1 1
1 1 2
2 1 3
3 1 4
4 2 1
5 2 2
6 2 3
7 2 4
8 3 3
9 4 3
0

输出样例：

3

在这一道题目中，需要注意使用二分图的最小（点）覆盖需要注意的地方：

• “0”条件：在二分图的同一个集合中，不可以有边
• “2”条件：在每一条边的两个端点中，必须选择一个

在这一道题目中，我把可以直接执行的任务不予考虑（在A或者B上在模式0就可以执行的任务，这样的任务不需要进行切换模式）

对于其他的工作，可以看做二分图中的边，这些边最少被A或者B执行，最小覆盖的选取的点就对应的是A，B机器需要切换的状态。

#include <bits/stdc++.h>
using namespace std;
int n, m, T;
#define N 105
vector<int> ver[N];
inline void add(int x, int y)
{
    ver[x].push_back(y);
}
int v[N];
int match[N];
bool dfs(int x)
{
    for(int i = 0; i < ver[x].size(); i++){
        int y = ver[x][i];
        if(v[y]) continue;
        v[y] = 1;
        if(dfs(match[y]) || !match[y]) {
            match[y] = x;
            return 1;
        }
    }
    return 0;
}
int main()
{
    while(cin >> n, n)
    {
        cin >> m >> T;
        for(int i = 0; i < n; i++) ver[i].clear();
        memset(match, 0, sizeof(match));
        for(int i = 1; i <= T; i++)
        {
            int asas, x, y;
            scanf("%d%d%d", &asas, &x, &y);
            if(!x || !y) continue;
            add(x, y);
        }
        int ans = 0;
        for(int i = 1; i <= n-1; i++)
        {
            memset(v, 0, sizeof(v));
            if(dfs(i)) ans ++;
        }
        cout << ans << "\n";
    }
    return 0;  
}

AcWing377. 泥泞的区域

在一块 N×M 的网格状地面上，有一些格子是泥泞的，其他格子是干净的。
现在需要用一些宽度为 1、长度任意的木板把泥地盖住，同时不能盖住干净的地面。
每块木板必须覆盖若干个完整的格子，木板可以重叠。
求最少需要多少木板。

输入格式

第一行包含两个整数 N 和 M。

接下来 N 行，每行 M 个字符，用来描述地面，* 表示泥泞格子，. 表示干净格子，字符之间没有空格。

输出格式

输出一个整数，表示结果。

数据范围

1≤N,M≤50

输入样例：

4 4
*.*.
.***
***.
..*.

输出样例：

4

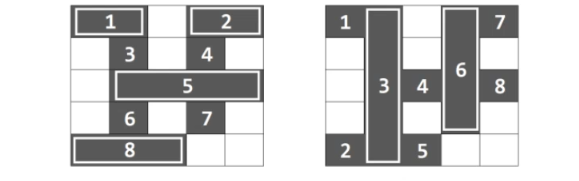
这里面仅仅询问到需要多少个木板，所以根据贪心策略，应该选择尽可能长的木板。

但是由于木板不可以在非泥泞的道路上进行放置，所以非泥泞的地方把木板进行了非分隔。

类似于算法竞赛进阶指南 0x68 二分图的匹配中的AcWing373. 車的放置
一个泥泞要么被横着的覆盖，要么被竖着的覆盖。所以满足“2”条件

首先，标出所有泥泞的方格横着的以及竖着的所属的标号。

然后把所有泥泞的方格的横着的编号以及竖着的编号进行链接

求这一个二分图的最小（点）覆盖

#include <bits/stdc++.h>
using namespace std;
#define N 56
int n, m;
int tot = 1;//这个就是方格的对应的代表值的计数
int a[N][N];//[i][j]的方格所属的横向长方体的序号
char s[N][N];
vector<int> ver[N*N*2];//因为tot的变化范围是2*N*N
inline void add(int x, int y)
{
    ver[x].push_back(y);
}
bool v[2*N*N];
int match[2*N*N];

bool dfs(int x)//匈牙利算法
{
    for(int i = 0; i < ver[x].size(); i++)
    {
        int y = ver[x][i];
        if(v[y]) continue;
        v[y] = 1;
        if(dfs(match[y]) || !match[y])
        {
            match[y] = x;
            return 1;
        }
    }
    return 0;
}

int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i++) scanf("%s", s[i] + 1);
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m+1; j++)//注意这里是m+1
        {
            if(s[i][j] == '*') a[i][j] = tot;//获得每一个格子所属横向格子的编号
            else tot++;
        }
    }
    int t = tot - 1;
    for(int j = 1; j <= m; j++)
    {
        for(int i = 1; i <= n+1; i++)
        {
            if(s[i][j] == '*') add(a[i][j], tot);//得到纵向格子的编号，并且构建二分图
            else tot++;
        }
    }
    int ans = 0;
    for(int i = 1; i <= t; i++)
    {
        memset(v, 0, sizeof(v));
        if(dfs(i)) ans++;
    }
    cout << ans;//二分图的最小覆盖就是最大匹配的边的数目。
    return 0;
}