63

温馨提示：点击题目标题即可跳转到OJ

树的直径

树上两点的距离：从一个点到另一个点的唯一一条路径的权值之和。

树的直径：任意选取两个点，距离最长的那个距离为这一棵树的直径。

树的最长链：距离最长的那个距离所对应的路径（有时候称为树的直径）

---

接下来的两种求法时间复杂度都是O（N）

如果是单纯求树的直径这一个数字，或者是有负权边，那么采用树形DP
如果要有具体的方案，采用两次DFS为妙。（在第二次的时候记录更新每一个点的点）
What‘s more? 如果使用两次DFS没有爆栈的风险！

树形DP

状态表示：d[i]，表示所有以i为根的树的深度。

状态转移：对于所有子树，有max(d[son]+edge[i])

这种是暴力枚举。对于一个最长链，肯定有一个层数最小的点。在这一个点处，就可以得到树的直径（最大路径）。
为d[son1]+d[son2]+edge1+edge2

有一种方法是求出son[x]+edge x，然后取前两个。

还有书上的思考如下：

可以枚举son1从1到t（子树的个数），son2从1到t，son1不等于son2，求d[son1]+d[son2]+edge1+edge2最大值。

由于具有对称性，所以枚举son1从1到t（子树的个数），son2从1到son1-1，求d[son1]+d[son2]+edge1+edge2最大值。

然后见代码

#define N 305
bool v[N];
int d[N];
int ans = 0;
void dp(int x)
{
    v[x] = 1;
    for(int i = head[x]; i; i = nxt[i])
    {
        int y = ver[y];
        int z = edge[i];
        if(v[y]) continue;
        dp(y);
        ans = max(ans, d[x] + d[y] + z);//在这个时候，d[x]仅仅是从1到i-1的最大值。
        //这相当于是枚举son1，取最大的son2属于从1到son1-1
        d[x] = max(d[x], z+d[y]);//更新d[x].
    }
}

两次BFS

第一次，任意选取一个点，求出与这一个点的最远距离的点p

第二次，选取p，求出与p最远的点q。

p到q的路径就是最长链。

证明：

---

AcWing350. 巡逻

在一个地区有 n 个村庄，编号为 1,2,…,n。

有 n−1 条道路连接着这些村庄，每条道路刚好连接两个村庄，从任何一个村庄，都可以通过这些道路到达其他任一个村庄。

每条道路的长度均为 1 个单位。

为保证该地区的安全，巡警车每天都要到所有的道路上巡逻。

警察局设在编号为 1 的村庄里，每天巡警车总是从警局出发，最终又回到警局。

为了减少总的巡逻距离，该地区准备在这些村庄之间建立 K 条新的道路，每条新道路可以连接任意两个村庄。

两条新道路可以在同一个村庄会合或结束，甚至新道路可以是一个环。

因为资金有限，所以 K 只能为 1 或 2。

同时，为了不浪费资金，每天巡警车必须经过新建的道路正好一次。

编写一个程序，在给定村庄间道路信息和需要新建的道路数的情况下，计算出最佳的新建道路的方案，使得总的巡逻距离最小。

输入格式

第一行包含两个整数 n 和 K。

接下来 n−1 行每行两个整数 a 和 b，表示村庄 a 和 b 之间有一条道路。

输出格式

输出一个整数，表示新建了 K 条道路后能达到的最小巡逻距离。

数据范围

3≤n≤100000,

1≤K≤2,

1≤a,b≤n

输入样例：

8 1 
1 2 
3 1 
3 4 
5 3 
7 5 
8 5 
5 6 

输出样例：

11

注意同一个点：题目中所说的是每一条道路全部巡逻一遍，而不是每一个点巡逻一遍。

注意：虽然是标记的“简单题”，但是如果直接想出来根本不可能。

网上的各种方法没有严谨的推倒。这里使用欧拉回路进行证明。

欧拉回路中，每一条边都只能被走1次，（原来的路可以认为是有无数条重边，新修的路仅仅只有一条）。

具有欧拉回路的充分必要条件是每一个点的度数均为偶度数。

对于原来的图

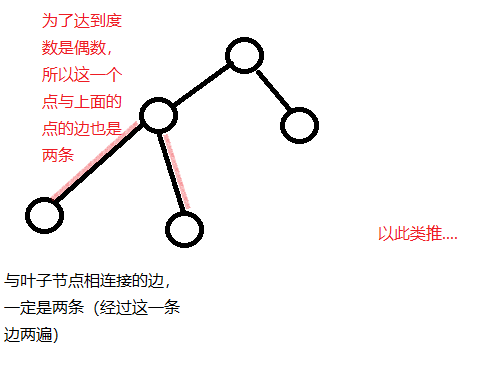
当在两个点之间连接了边之后，那么这两个点与父亲节点连接的边数应该是1（也可以是3,5...但是1最优）。

经过推理，恰好是两点之间的路径均走过一次。

如果是增加第二条边，那么重叠部分被减为0，与题意不符，所以必须再走这条边！

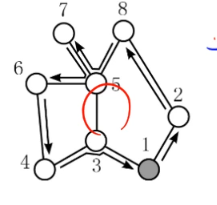
在3-5之间，不能是0条边，应该是2条边。

即，在重叠部分，走过的仍然是2遍。恰好把第一次的最长的边给抵消了。

由此，我们可以得到解题的思路。

第一次，采用BFS进行遍历，并求出方案数。得到最长路径\(L_1\)然后把最长链上的值改为-1.

第二次，由于有负边权的加入，所以使用树形DP，得到最长路径（直径）\(L_2\)

最终结果是\(2\times (n-1)-L_1-L_2+1+1\)

#include <bits/stdc++.h>
using namespace std;
#define N 100005
int n, k;
int head[N], tot;
int ver[N*2], edge[N*2], nxt[N*2];
int pre[N];
queue<int > q;//仅仅供bfs使用，在每一次使用之后，
//这一个队列会清空，所以不需要进行初始化
int d[N];
int L2 = 0;
inline void add(int x, int y)
{
    ver[++tot] = y;
    edge[tot] = 1;
    nxt[tot] = head[x];
    head[x] = tot;
}
int bfs(int w)
{
    memset(d, -1, sizeof(d));
    q.push(w);
    d[w] = 0;
    while(!q.empty())
    {
        int x = q.front();
        q.pop();
        for(int i = head[x]; i; i = nxt[i])
        {
            int y = ver[i];
            if(d[y] != -1) continue;
            d[y] = d[x] + 1;
            pre[y] = i;
            q.push(y);
        }
    }
    int p = w;
    for(int i = 1; i <= n; i++) 
        if(d[i] > d[p]) p = i;
    return p;
}
void update(int p, int q)
{
    while(p != q)
    {
        edge[pre[q]] = -1;
        edge[pre[q]^1] = -1;
        q = ver[pre[q]^1];
    }
}
int dp(int x, int fa)
{
    for(int i = head[x]; i; i = nxt[i])
    {
        int y = ver[i];
        if(y == fa) continue;
        dp(y, x);
        L2 = max(L2, d[x] + d[y] + edge[i]);
        d[x] = max(d[x], d[y] + edge[i]);
    }
    return L2;
}
int main()
{
    tot = 1;//这样可以使用成对变化。
    scanf("%d%d", &n, &k);
    for(int i = 1; i <= n-1; i++)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);
        add(b, a);
    }
    int p = bfs(1);
    int q = bfs(p);
    int ans = 2*(n-1) + 1 - d[q];
    if(k == 1)
    {
        printf("%d\n", ans);
        //cout << p <<"  " << q;
        return 0;
    }
    update(p, q);
    memset(d, 0, sizeof(d));
    ans = ans - dp(1, 0) + 1;
    printf("%d\n", ans);
  
    return 0;
}

AcWing351. 树网的核

设 T=(V,E,W) 是一个无圈且连通的无向图（也称为无根树），每条边带有正整数的权，我们称 T 为树网（treenetwork），其中 V,E 分别表示结点与边的集合，W 表示各边长度的集合，并设 T 有 n 个结点。

路径：树网中任何两结点 a,b 都存在唯一的一条简单路径，用 d(a,b) 表示以 a,b 为端点的路径的长度，它是该路径上各边长度之和。

我们称 d(a,b) 为 a,b 两结点间的距离。

一点 v 到一条路径 P 的距离为该点与 P 上的最近的结点的距离：

d(v，P)=min{d(v，u)}，u 为路径 P 上的结点。

树网的直径：树网中最长的路径称为树网的直径。

对于给定的树网 T，直径不一定是唯一的，但可以证明：各直径的中点（不一定恰好是某个结点，可能在某条边的内部）是唯一的，我们称该点为树网的中心。

偏心距 ECC(F)：树网 T 中距路径 F 最远的结点到路径 F 的距离，即：

ECC(F)=max{d(v,F),v∈V}

任务：对于给定的树网 T=(V,E,W) 和非负整数 s，求一个路径 F，它是某直径上的一段路径（该路径两端均为树网中的结点），其长度不超过 s（可以等于 s），使偏心距 ECC(F) 最小。

我们称这个路径为树网 T=(V,E,W) 的核（Core）。

必要时，F 可以退化为某个结点。

一般来说，在上述定义下，核不一定只有一个，但最小偏心距是唯一的。

输入格式

包含 n 行： 第 1 行，两个正整数 n 和 s，中间用一个空格隔开，其中 n 为树网结点的个数，s 为树网的核的长度的上界，设结点编号依次为 1,2,…,n。

从第 2 行到第 n 行，每行给出 3 个用空格隔开的正整数，依次表示每一条边的两个端点编号和长度。

例如，2 4 7 表示连接结点 2 与 4 的边的长度为 7。

所给的数据都是正确的，不必检验。

输出格式

只有一个非负整数，为指定意义下的最小偏心距。

数据范围

n≤500000,s<231

输入样例：

5 2
1 2 5
2 3 2
2 4 4
2 5 3

输出样例：

5

在这一道题目中，从题目中所给出的性质入手：

一棵树如果存在多条直径，那么这些直径一定有重叠的公共部分（可能是一条路径，也可能是一个点）

证明：反证法

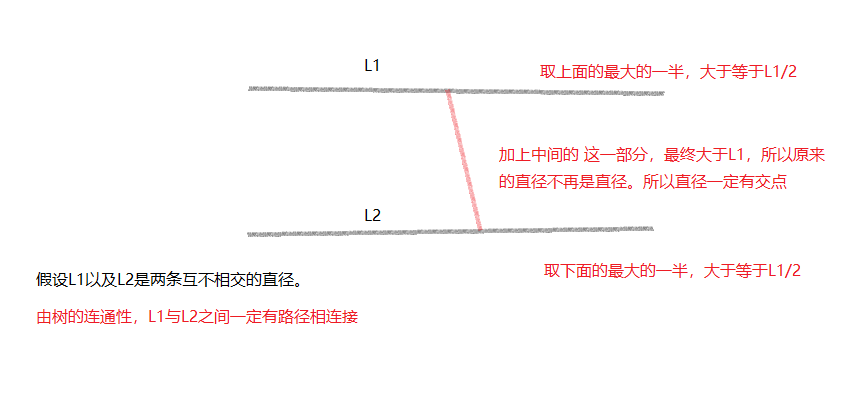
由于树连通并且无环，所以公共的部分不可能是分开，即公共的部分一定是一体的。

---

然后证明：树网的偏心距与所选取的直径并没有关系。

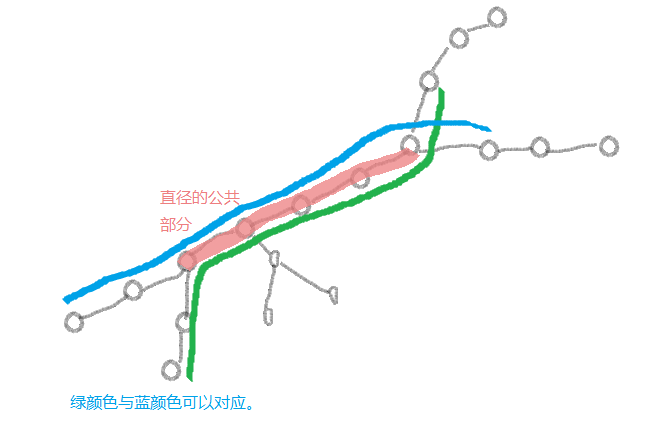
连接在公共部分的与说选取的直径没有关系。绿颜色（黄颜色）到直径的末端距离由于是对称的，所以也相等。

由此可见，对于所有的直径，情况全部是唯一的。

所以我们仅仅需要考虑一条直径

一下是思维的跳跃

思路一\(O(n^3)\)

直接枚举一条直径的两个端点i和j，并且对于每一种情况求得偏心距。

思路二\(O(n^2)\)

由贪心算法可以知道，所选取的“核”越长越好。

思路三\(O(nlogL)\)

二分答案。

合理性检验方法：

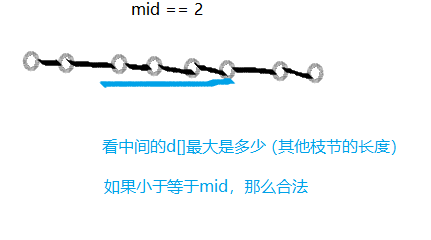
思路四\(O(n^)\)

如果每一次都进行遍历，明显做了许多的无用功。所以使用d[]存起来。

根据思路二，采用d[]数组，就可以求出答案

同时得到了下一种的优化，即不用滑动窗口。

终极思路：并不需要枚举，最好的答案一定是把“核”放到中间

通过思路四的优化可以得知。

代码实现

#include <bits/stdc++.h>
using namespace std;
#define N 500005
int head[N], tot;
int ver[N*2], nxt[N*2], edge[N*2];
inline void add(int x, int y, int z)
{
    ver[++tot] = y;
    edge[tot] = z;
    nxt[tot] = head[x];
    head[x] = tot;
}
int n, s;
int d[N];
bool v[N];
queue<int> q;
int path[N], cntpath, pre[N];
int b[N], sum[N];//b表示每一条边的大小，sum表示前缀和。
int bfs(int w)
{
    memset(d, 0, sizeof(d));
    memset(v, 0, sizeof(v));
    q.push(w), v[w] = 1;
    while(q.size())
    {
        int x = q.front();
        q.pop();
        for(int _ = head[x]; _; _ = nxt[_])
        {
            int y = ver[_], z = edge[_];
            if(v[y]) continue;
            d[y] = d[x] + z;
            v[y] = 1;
            pre[y] = _;
            q.push(y);
        }
    }
    int p = w;
    for(int i = 1; i <= n; i++) 
        if(d[p] < d[i]) p = i;
    return p;
}
void updatepath(int p, int q)
{
    while(p != q)
    {
        path[++cntpath] = q;
        q = ver[pre[q]^1];
    }
    path[++cntpath] = q;
    for(int i = 1; i <= cntpath - 1; i++)
    {
        b[i+1] = edge[pre[path[i]]];
    }
    for(int i = 1; i <= cntpath; i++) sum[i] += sum[i-1] + b[i];
}
int dfs(int x)
{
    v[x] = 1;
    for(int i = head[x]; i; i = nxt[i])
    {
        int y = ver[i], z = edge[i];
        if(v[y]) continue;
        dfs(y);
        d[x] = max(d[x], d[y] + z);
    }
    return d[x];
}
int main()
{
    tot = 1;
    scanf("%d%d", &n, &s);
    for(int i = 1; i <= n-1; i++)
    {
        int x, y, z;
        scanf("%d%d%d", &x, &y, &z);
        add(x, y, z);
        add(y, x, z);
    }
    //找到一条直径
    int p = bfs(1);
    int q = bfs(p);
    updatepath(p, q);//更新path，顺便处理前缀和
    //开始处理直径上所有点的邻接的偏心距
    int maxh = 0;
    memset(v, 0, sizeof(v));
    memset(d, 0, sizeof(d));
    for(int i = 1; i <= cntpath; i++) v[path[i]] = 1;
    for(int i = 1; i <= cntpath; i++) maxh = max(maxh, dfs(path[i]));

    int lastj = 0;
    int ans = 1 << 30;
    for(int i = 1, j = 1; i <= cntpath; i++)
    {
        while(j < cntpath && sum[j+1]-sum[i] <= s) j++;
        if(sum[cntpath]-sum[j] <= sum[i])
        {
            ans = min(ans, max({maxh, sum[cntpath]-sum[j], sum[i]}));
            if(lastj)
            {
                ans = min(ans, max({maxh, sum[cntpath]-sum[lastj], sum[i-1]}));
            }
            break;
        }
        lastj = j;
    }
    printf("%d", ans);

    return 0;
}

最近公共祖先

在一棵树中，

公共祖先：两个点所共有的祖先。

最近公共祖先（LCA）：在所以祖先中，深度最深的。

所具备的性质：

1. 在所以的公共祖先中，深度最深。
2. 两个点到达根节点的路径上的交汇点。
3. 两点之间路径上的最浅的点。

---

有三种求法

向上标记法（一步一步走）

x向上标记到达根节点的路径，y也向上标记，与x的标记交会的点就是LCA。

树上倍增法（如果向上标记，太过于慢，倍增！）

注意：有两个性质

1. 满足单调性。如果x与y向上走，走的太远，以至于超越了LCA，那么是到达的同一点。（默认走的超过根节点全部是0号节点）。
2. 满足可加性。走\(k_1\)步到达某一个点，从这一个点走\(k_2\)步到达最终的点，与从最初的点走\(k_1+k_2\)相同。

构建需要\(nlogn\)

查询需要\(logn\)

代码实现：

#include <bits/stdc++.h>
using namespace std;
#define N 305
int head[N], tot;
int ver[N*2], nxt[N*2];
int n;
int d[N], f[N][21];//d既是深度的标记，也是访问以及没有访问的标记。
queue<int > q;
inline void add(int x, int y)
{
    ver[++tot] = y;
    nxt[tot] = head[x];
    head[x] = tot;
}
void bfs(int w)//nlogn
{
    d[w] = 1;
    q.push(w);
    while(q.size())
    {
        int x = q.front();
        q.pop();
        for(int i = head[x]; i; i = nxt[i])
        {
            int y = ver[i];
            if(d[y]) continue;
            d[y] = d[x] + 1;
            q.push(y);
            f[y][0] = x;
            for(int k = 1; k <= 19; k++) f[y][k] = f[ f[y][k-1] ][k-1];
        }
    }
}
int lca(int x, int y)
{
    if(d[x] < d[y]) swap(x, y);
    for(int i = 19; i >= 0; i--)
        if(d[f[x][i]] >= d[y]) x = f[x][i];
    if(x == y)return x;
    for(int i = 19; i >= 0; i--)
        if(f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];
    return f[x][0];
}
int main()
{
    tot = 1;
    scanf("%d", &n);
    for(int i = 1; i <= n; i++)
    {
        int x, y;
        scanf("%d%d", &x, &y);
        add(x, y);
        add(y, x);
    }
    bfs(1);
    return 0;
}

AcWing391. 聚会

Y 岛风景美丽宜人，气候温和，物产丰富。Y 岛上有 N 个城市（编号 1,2,…,N），有 N−1 条城市间的道路连接着它们。

每一条道路都连接某两个城市。

幸运的是，小可可通过这些道路可以走遍 Y 岛的所有城市。

神奇的是，乘车经过每条道路所需要的费用都是一样的。

小可可，小卡卡和小 YY 经常想聚会，每次聚会，他们都会选择一个城市，使得 3 个人到达这个城市的总费用最小。

由于他们计划中还会有很多次聚会，每次都选择一个地点是很烦人的事情，所以他们决定把这件事情交给你来完成。

他们会提供给你地图以及若干次聚会前他们所处的位置，希望你为他们的每一次聚会选择一个合适的地点。

输入格式

第一行两个正整数，N 和 M，分别表示城市个数和聚会次数。

后面有 N−1 行，每行用两个正整数 A 和 B 表示编号为 A 和编号为 B 的城市之间有一条路。

再后面有 M 行，每行用三个正整数表示一次聚会的情况：小可可所在的城市编号，小卡卡所在的城市编号以及小 YY 所在的城市编号。

输出格式

一共有 M 行，每行两个数 Pos 和 Cost，用一个空格隔开，表示第 i 次聚会的地点选择在编号为 Pos 的城市，总共的费用是经过 Cost 条道路所花费的费用。

数据范围

N≤500000,M≤500000

输入样例：

6 4
1 2
2 3
2 4
4 5
5 6
4 5 6
6 3 1
2 4 4
6 6 6

输出样例：

5 2
2 5
4 1
6 0

如果询问两个人聚会，应该怎么走，这样的话，相聚的点必定在两点的路径上，并且任意一点都可以。

如果可以得到每一个节点的LCA，任意两点的距离就是这两点的深度减去LCA(x, y)的深度的两遍

代码实现

#include <bits/stdc++.h>
using namespace std;
#define N 500005
int head[N], tot;
int ver[N*2], nxt[N*2];
int n, m;
int d[N], f[N][21];
queue<int>q;
inline void add(int x, int y)
{
    ver[++tot] = y;
    nxt[tot] = head[x];
    head[x] = tot;
}
void bfs(int w)
{
    d[w] = 1;
    q.push(w);
    while(q.size())
    {
        int x = q.front();
        q.pop();
        for(int i = head[x]; i; i = nxt[i])
        {
            int y = ver[i];
            if(d[y]) continue;
            d[y] = d[x] + 1;
            q.push(y);
            f[y][0] = x;
            for(int k = 1; k <= 19; k++)
            {
                f[y][k] = f[ f[y][k-1] ][k-1];
            }
        }
    }
}
int lca(int x, int y)
{
    if(d[x] < d[y]) swap(x, y);
    for(int i = 19; i >= 0; i--) if(d[f[x][i]] >= d[y]) x = f[x][i];
    if(x == y) return x;
    for(int i = 19; i >= 0; i--)
        if(f[x][i] != f[y][i]) x = f[x][i], y = f[y][i];
    return f[x][0];
}
inline int dist(int x, int y)
{
    int lc = lca(x, y);
    return d[x] + d[y] - d[lc] * 2;
}
int main()
{
    tot = 1;
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n-1; i++)
    {
        int x, y;
        scanf("%d%d", &x, &y);
        add(x, y);
        add(y, x);
    }
    bfs(1);
    //for(int i = 1; i <= n; i++)printf("\n\t%d", d[i]);
    //cout << "tot" << tot;
    for(int xx = 1; xx <= m; xx ++)
    {
        int lc = 0;
        int a[5];
        for(int i = 1; i <= 3; i++) scanf("%d", a+i);
        lc = lca(a[1], a[3]);
        for(int i = 1; i <= 2; i++)
        {
            int tmp = lca(a[i], a[i+1]);
            if(d[tmp] > d[lc]) lc = tmp;
        }
        int ans = 0;
        for(int i = 1; i <= 3; i++) ans += dist(a[i], lc);
        printf("%d %d\n", lc, ans);
    }
    return 0;
}

Tarjan算法（与并查集的路径压缩相似）

这是一个离线算法！

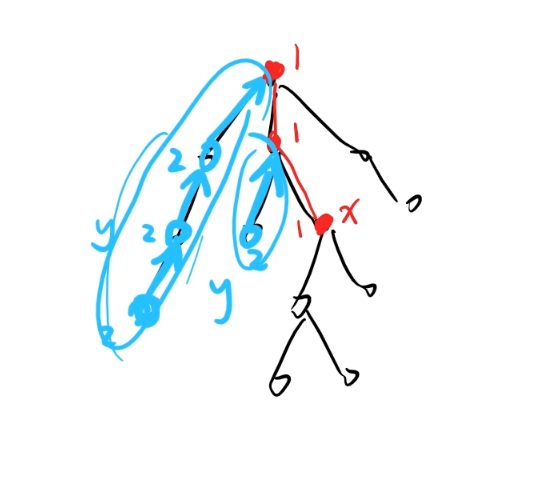
这里的v数组不再是只有0和1.

在这里有三种状态：0,1,2。

0：还没有被访问过。

1：正在访问的点以及这个点到根节点上的所有点。

2：已经被访问的点。

在任何时候，2号点的最终父亲是1号节点。

这一个过程就像是并查集。所以采用路径压缩在进行求

值得注意的是：

1. 对于x，y（不相等），那么如果遍历到x的时候y是0，那么遍历到y的时候x是2.
   反着对于x以及y，正着与反着都考虑一下总有答案。
2. 当x以及y相等的时候，就不向邻接表中存了，直接把答案记作x。

AcWing391的Tarjan算法实现。（例题见上一题）

（使用邻接表的形式对数据进行离线化）