GNN起步 ？——GNN变体以及框架

一、 GraphSAGE

GraphSAGE从两个方面对GCN进行了改动，一方面是通过采样邻域策略将GCN全图（full batch）的训练方式改造成以结点为中心的小批量（mini batch）训练方式，这使得大规模图数据的分布式训练成为可能；另一方面是该算法对聚合邻居操作进行了拓展，提出了替换GCN操作的几种新的方式。

1.1 采样邻居

在之前的GCN模型中，训练方式是一种全图形式，也就是一轮迭代，所有节点的样本损失只会贡献一次梯度数据，无法做到DNN中通常用到的小批量式更新，这从梯度更新的次数而言，效率是很低的。采用小批量的训练方法对大规模的图数据的训练进行分布式拓展是十分必要的。GraphSAGE从聚合邻居的角度出发，对邻居进行随机采样来控制实际运算的结点k阶子图的数据规模，在此基础上对采样子图进行随机组合来完成小批量式的训练。

在GCN模型中，我们知道结点在第（k+1）层的特征只与其邻居在k层的特征有关，这种局部性质使得结点在第k层的特征只与自己的k阶子图有关。

根据上述阐述，我们只需要考虑结点的k阶子图就可以完成对结点的高层特征的计算。但是对于一个大规模的图数据来说，我们直接将此思路迁移过来仍然存在以下两个问题：

（1）子图的结点数存在指数级增长的问题。假设图中节点度的均值为d，执行k层GCN，则k阶子图平均出现1+d+d²+……+d^k个结点，如果d=10，k=4，那么就有11111个结点要参与计算，这会导致很高的计算复杂度。

（2）真实世界中图节点数据存在的度往往呈现幂律分布，一些结点的度会非常大，我们称这样的节点为超级节点，在很多图计算的问题中，超级节点都是比较难处理的对象。在这里，由于超级节点本身邻居的数目很大，再加上子图结点数呈指数级增长的问题，这种类型的结点高层特征计算的代价会变得更加高昂。

 

对于上述两种情况的出现，GraphSAGE采用了非常自然的采样邻居的操作来控制子图发散时的增长率。具体做法如下：设每个节点在第k层的邻居采样倍率为S_k（该参数为GraphSAGE算法的超参数，由用户自行设计调节），即每个结点采样的一阶邻居总数不超过S_k，那么对于任意一个中心节点的表达计算，所涉及的总点数将在o(∏^k_k=1S_k)这个级别。这里对于节点采样，GraphSAGE选择了均匀分布，事实上可以根据工程效率或者业务背景采用其他形式的分布代替均匀分布。

1.2 聚合邻居

GraphSAGE研究了聚合邻居操作所需要的性质，并且提出了几种新的聚合操作，需满足如下条件：

（1） 聚合操作必须要对聚合节点的数量做到自适应。不管结点的邻居数量怎么变化，进行聚合操作后输出的维度必须是一致的，一般是一个统一长度的向量。

（2）聚合操作对结点具有排列不变性。对于我们熟悉的2D图像数据和1D序列数据，前者包含着空间顺序，后者包含着时间顺序，但是图数据本身是一种无序的数据结构，对于聚合操作而言，这就要求不管邻居节点的排列顺序如何，输出结果总是一样的。比如Agg（v₁,v₂） = Agg（v₂,v₁）。

当然，从模型优化的层面看，这种聚合操作还必须是可导的。有了上述性质的保证，聚合操作就能对任意输入的节点集合做到自适应。比较简单的符合要求的算子有：

（1）平均/加和聚合算子

（2）池化聚合算子

1.3 算法过程

看看该算法实现小批量训练形式的具体过程。

 

 

 

 

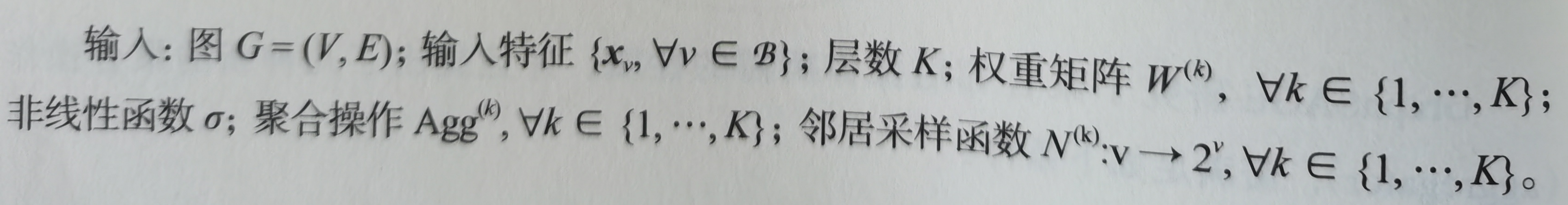
上述算法的基本思路是先将小批集合B内的中心节点聚合操作所要涉及到的k阶子图一次性全部遍历出来，然后在这些结点上进行K次聚合的迭代式结算。算法的1~7行描述遍历操作。可以这样理解：要想得到某个中心节点的第k层的特征，就需要采样第（k-1）层的邻居，然后对第（k-1）层的每个节点采样其第（k-2）层的邻居，以此类推，直到采样完第1层的所有邻居为止。需要注意的是，每层的采样函数可以单独设置。

第9~11行是第二步——聚合操作，其核心体现在第11~13行的3个公式上面。第11行的式子是调用聚合操作完成对每个节点邻居特征的整合输出，第12行是将聚合后的邻居特征与中心节点的上一层特征进行拼接，然后送到一个单层网络中得到中心节点新的特征向量，第13行对节点的特征向量进行归一化处理，将节点所有的向量都统一到单位尺度上。对这3行的操作迭代K次就完成了对B内所有中心节点的特征向量提取。