论文笔记：LGLMF: Local Geographical based Logistic Matrix Factorization Model for POI Recommendation

Rahmani, Hossein A., et al. “LGLMF: Local Geographical Based Logistic Matrix Factorization Model for POI Recommendation.” Asia Information Retrieval Symposium, 2019, pp. 66–78.

摘要：随着基于位置的社交网络的快速发展，个性化兴趣点 (POI) 推荐已成为帮助用户探索周围环境的关键任务。由于签到数据的稀缺性，地理信息的可用性为提高 POI 推荐的准确性提供了机会。此外，矩阵分解方法提供了可用于 POI 推荐的有效模型。然而，为了提高 POI 推荐方法的性能，应该解决两个主要挑战。首先，利用地理信息来捕捉用户的个人、地理概况和位置的地理流行度。其次，将地理模型纳入矩阵分解方法。针对这些问题，本文提出了一种基于本地地理模型的 POI 推荐方法，该方法同时考虑了用户和位置的观点。为此，通过考虑用户的主要活动区域以及该区域内每个位置的相关性，提出了一个有效的地理模型。然后，将提出的本地地理模型融合到 Logistic Matrix Factorization 中，以提高 POI 推荐的准确性。在两个众所周知的数据集上的实验结果表明，所提出的方法优于其他最先进的 POI 推荐方法。

 

从摘要可以看出，本篇论文主要提出的创新点是 同时考虑用户和POI的观点，将捕捉到的信息融入 Logistic Matrix Factorization 中。

 

在推荐方法中，数据稀疏是一个很大的问题。对于POI推荐来说，面对巨量的POI，每个用户访问过的POI是极其有限的。本文通过将地理影响建模为重要的上下文信息，在所提出的方法中解决了稀疏问题的。

 

本文所提出的 POI 推荐方法，称为基于本地地理的 Logistic 矩阵分解 (LGLMF)。 LGLMF 包括两个主要步骤。 第一步，基于用户和位置的观点提出本地地理模型（LGM）。 然后，在第二步中，将 LGM 融合为逻辑矩阵分解 (LMF) 方法。 融合矩阵分解模型用于预测用户的偏好。

所以算法模型主要由两部分组成：Local Geographical Model 和 Logistic Matrix Factorization融合Local Geographical Model中获得的user-POI偏好。

现在逐个看一下这两个模块：

1. Local Geographical Model

定义用户集：U={u₁,u_2……u_m}

定义POI集：P={p₁,p_2……p_n}

令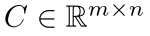是一个用户-POI 签到频率矩阵，其中有 m 个用户和 n 个 POI。矩阵中的每个值表示用户u 到POI p 的签到频率。

 

接下来引出两个定义：

 

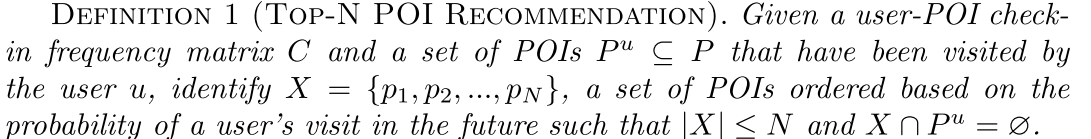
 即X是用户u未来可能访问的POI的集合，X的数量是≤用户u曾经访问过的POI的数量的，且用户u未来可能去的POI不是该用户曾经访问过的POI中的。

 

 

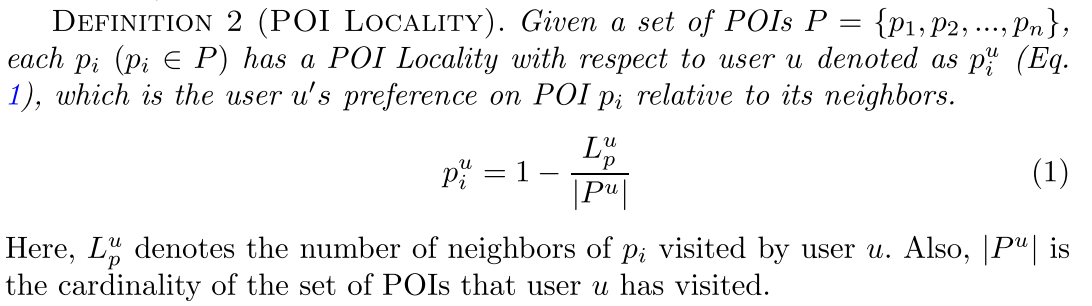
 此处定义POI的地理影响。当用户u访问过POI p_i时，用户会对该POI周围一定范围内的POI感兴趣。

            用户u访问过的POI p_i的邻居数量

p^u_i=1 -  ——————————————

            用户u访问过的POI的数量和

算法流程：

 

 该算法由三个内循环组成，用于对地理信息进行建模，前两个循环对用户所在区域（第 2 - 5 行）进行建模，第三个循环计算考虑到对邻近 POI 的访问，用户更喜欢邻里内的 POI（第 6 - 10 行）。为了对用户的区域建模，我们需要找到每个用户的高活动位置（在现实世界中，这可能是用户的居住区域）。为此，用户最常签到的 POI 被用来推断他/她的高活动位置（第 1 行）。然后，我们扫描未访问的 POI 列表，以找到那些位于该用户的同一区域（区域内）内的 POI，即距离用户高活动位置（用户的角度）α 公里以内的那些（第 5 行）。此外，基于每个用户的区域内 POI，我们考虑签入的邻近 POI 的影响，这些 POI 与未访问的 POI 的距离小于 γ 米（位置的视角）（第 7-10 行）。

最终获得一个用户-POI偏好矩阵，此矩阵结合了用户和POI的角度。

2. Logistic Matrix Factorization

个人感觉这一步需要一些item-based的知识积累：通常，基于 MF 的推荐的目标是找到两个低秩矩阵，包括用户因素矩阵 V ∈ R^mxk 和项目因素矩阵 L ∈ R^mxk，其中 k 是潜在因素的数量，使得内部 这两个矩阵的乘积近似矩阵Cˆ，即 Cˆ = V × L^T。 V (vu ∈ V) 的每一行代表用户行为的用户向量，L (lp ∈ L) 的每一行代表物品属性的行为。

本算法中用户u和POI p的矩阵分解同理。

所以用户U对POI p的偏好定义为：

 

 

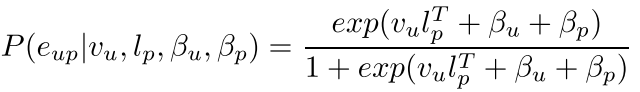
取对数更方便计算，所以最终的目标函数为：

 

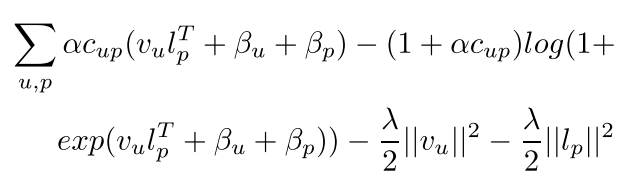
 然后如论文所说，结合上二者的影响：

 

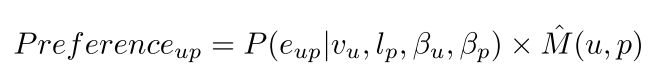
 本文提出的算法基本就是这样。