2024（AtCoder Beginner Contest 375）

D ABA

题目链接：https://atcoder.jp/contests/abc375/tasks/abc375_d

题目大意：给定一个字符串S，让你在其中选择三个严格递增的下标，(i,j,k) 使得S[i] + S[j] + S[k] 连接在一起的字符串是一个回文串，问，有多少种选法。

eg.

---

input: 

ABCACC

output:

5

---

可以选择 (1,2,4),(1,3,4),(3,4,5),(3,4,6),(3,5,6) 共计五种。

分析：

  三个字符组成的回文串，无非就是只要首尾一样即可，中间是任意的，比如 ABA,AAA,AXA等等。对于每一个种字母我们都是可以算这种字符对答案的贡献。

具体怎么计算呢？，比如字符串ABACA ，出现了3种字符，假如我们要构造首尾为A的回文串的话，一定是在所有A出现的位置上去选择‘首’和‘尾’。

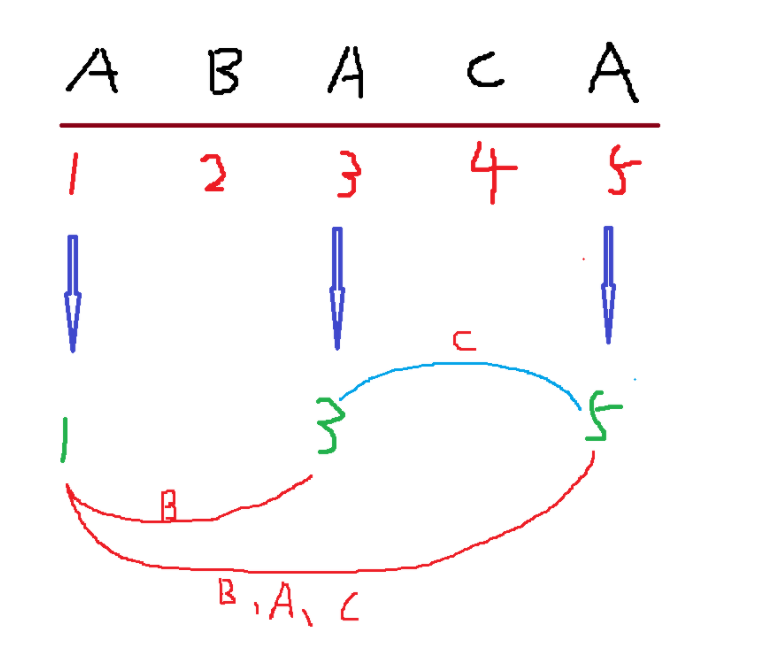
如图：A在1，3，5，出现了，那么选择‘首’和‘尾’的情况就有，(1,3)，(1,5)，(3,5) 三种情况。对于每一个区间，可以产生的种类数也就是‘首’和‘尾’之间的字母个数。

所以我们对于一种字母对答案的贡献，就是把它们能构造的所有首尾情况的能产生的种类数全部加起来，而我们的最终答案就是把所有种类的字母对答案的贡献加起来就行了。

代码如下：

#include <bits/stdc++.h> 
using namespace std;
typedef long long ll;	
int main(){
	string aa;
	map<char,vector<int> > mp;//维护每种字符出现的位置;
	ll ans = 0;
	cin >> aa;
	for (int i = 0;i < aa.size();i++){
		mp[aa[i]].push_back(i);
	}
	
	for(auto &c : mp){
		ll len =  c.second.size();
		vector<ll> sum(len + 2,0);//维护每种字符出现的位置后缀和 
		
		for (int i = len - 1,j = len;i >= 0;i--,j--){//求后缀和
			sum[j] = sum[j + 1] + c.second[i];
		}
		
		ll temp = 0;//记录一种字母的贡献和 
		for (int i = 1;i <= len - 1;i++){
			temp += sum[i + 1] - (len - i) * (c.second[i - 1] + 1); 
		}
		ans += temp;
	}
	cout << ans << endl;
	return 0;
}

 

---

补充一下为什么里面temp += sum[i + 1] - (len - i) * (c.second[i - 1] + 1);  就可以算出答案，先看下图：

假如某一种字符的在原字符串出现的位置线性集合为N，所以每个位置就是N[1],N[2],,,,,,N[n]。

---

---

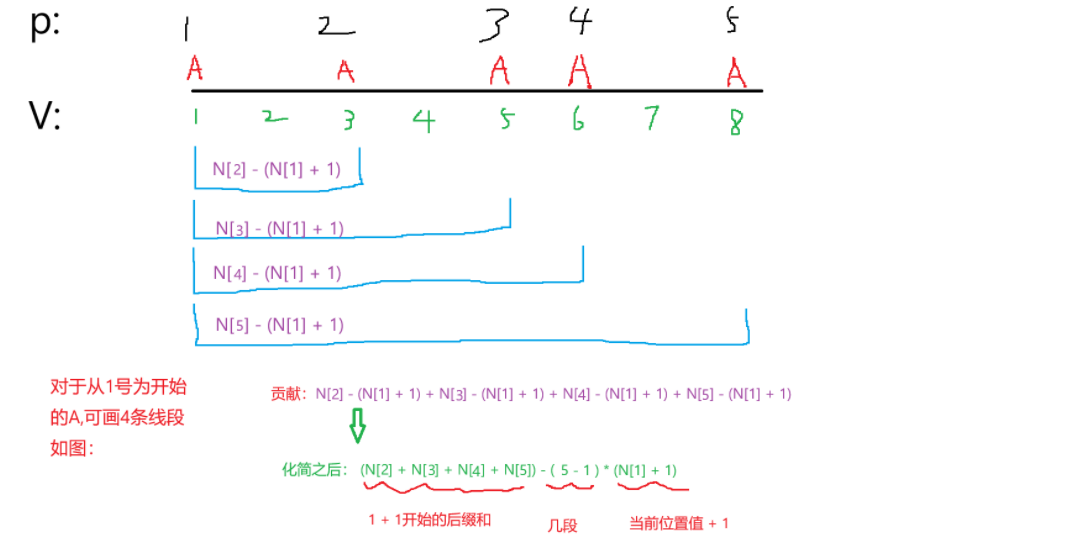
比如从第一个A开始能构造4段也就是 len - 当前位置，那么我们会发现每次都是减去（N[1] + 1）也就是（当前位置的值 + 1，至于为什么算之间隔了多少字母要 尾 - （首 + 1），可以下去画一画）。化简之后会发现，如果从某个位置算的话，这部分答案就是下一个位置的 值后缀和  -（总长度 - 当前位置 ）* （当前位置的值 + 1），在图上也就是所有蓝色区间的答案。

注意这个例子仅仅示例了对于字符A来说从1号为A开始的答案贡献，后面位置的也是同理，所以上面程序里面，是遍历了1到len - 1的每一个位置的（ 也就是  for (int i = 1;i <= len - 1;i++)    ）。

 

 

 

C - Spiral Rotation

题目链接：C - Spiral Rotation (atcoder.jp)C - Spiral Rotation (atcoder.jp)

题目大意：

  给你一个n * n 的字符串方阵，每次会将图案顺时针旋转，而每次旋转后就会剥夺最外层的旋转权力，就像一层一层剥洋葱皮一样的剥夺。问最后旋转完之后的图案长啥样。

eg.

input:

8
.......#
.......#
.####..#
.####..#
.##....#
.##....#
.#######
.#######

  

---

output:

........
#######.
#.....#.
#.###.#.
#.#...#.
#.#####.
#.......
########

---

示例过程：

.......#   ........   ........   ........   ........
.......#   ######..   #######.   #######.   #######.
.####..#   ######..   #....##.   #.....#.   #.....#.
.####..# → ##..##.. → #....##. → #.##..#. → #.###.#.
.##....#   ##..##..   #..####.   #.##..#.   #.#...#.
.##....#   ##......   #..####.   #.#####.   #.#####.
.#######   ##......   #.......   #.......   #.......
.#######   ########   ########   ########   ########

---

分析：

  对于一个位置，要知道，如果我们将它顺时针转4次的话，就会变回原来的位置。那么我们对于每一个点，得是，只要知道 每个点总共的旋转次数 % 4  就是每个点 真正只需要的旋转次数。再去分类讨论0、1、2、3的情况就行了。

---

代码：

#include <bits/stdc++.h> 
using namespace std;
typedef long long ll;
const ll maxn = 5000;
char aa[maxn][maxn];//原方阵 
char bb[maxn][maxn];//答案方阵 
int main(){
	int n;
	cin >> n;
	for (int i = 1;i <= n;i++){
		for (int j = 1;j <= n;j++){
			cin >> aa[i][j];
		}
	}
	for (int i = 1;i <= n;i++){
		for (int j = 1;j <= n;j++){
			int all = min(min(i,n - j + 1),min(n - i + 1,j)) % 4;//操作总数 % 4 
			
			if (all == 0) bb[i][j] = aa[i][j];//不转 
			
			else if (all == 1) bb[i][j] = aa[n - j + 1][i];//转一次 
			
			else if(all == 2) bb[i][j] = aa[n - i + 1][n - j + 1];//两次 
			
			else if (all == 3) bb[i][j] = aa[j][n - i + 1];//3次 
			
			cout << bb[i][j];
		}cout << endl;
	}
	return 0;
}