线性回归

一、一元线性回归

 导入第三方模块
import statsmodels.api as sm
sm.ols(formula, data, subset=None, drop_cols=None)
formula：以字符串的形式指定线性回归模型的公式，如'y~x'就表示简单线性回归模型
data：指定建模的数据集
subset：通过bool类型的数组对象，获取data的子集用于建模
drop_cols：指定需要从data中删除的变量

　　

# 导入第三方模块
import pandas as pd
import statsmodels.api as sm
income = pd.read_csv('Salary_Data.csv')
# 利用收入数据集，构建回归模型
fit = sm.formula.ols('Salary ~ YearsExperience', data = income).fit()
# 返回模型的参数值
fit.params
out:
Intercept 25792.200199
YearsExperience 9449.962321
dtype: float64

　　

二、多元线性回归

# 导入模块
from sklearn import model_selection
# 导入数据
Profit = pd.read_excel(r'D:\pylearn\11\Predict to Profit.xlsx')
# 将数据集拆分为训练集和测试集
train, test = model_selection.train_test_split(Profit, test_size = 0.2, random_state=1234)
# 根据train数据集建模
model = sm.formula.ols('Profit ~ RD_Spend+Administration+Marketing_Spend+C(State)', data 
= train).fit()
print('模型的偏回归系数分别为：\n', model.params)
# 删除test数据集中的Profit变量，用剩下的自变量进行预测
test_X = test.drop(labels = 'Profit', axis = 1)
pred = model.predict(exog = test_X)
print('对比预测值和实际值的差异：\n',pd.DataFrame({'Prediction':pred,'Real':test.Profit}))

/*默认情况下，对于离散变量State而言，模型选择California值作为对照组。*/

结果：
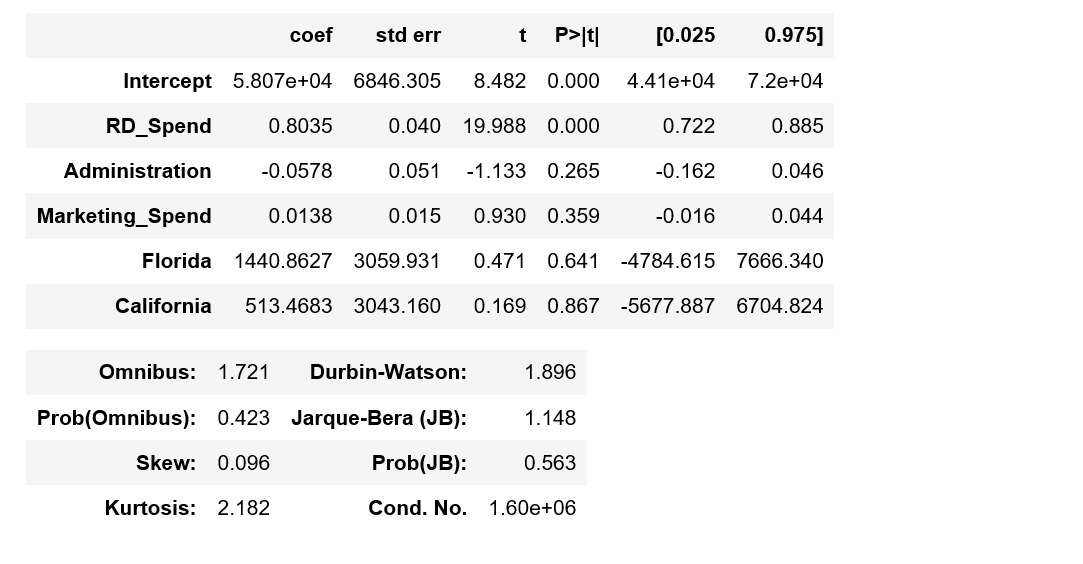
模型的偏回归系数分别为：
 Intercept               58581.516503
C(State)[T.Florida]       927.394424
C(State)[T.New York]     -513.468310
RD_Spend                    0.803487
Administration             -0.057792
Marketing_Spend             0.013779
dtype: float64
对比预测值和实际值的差异：
        Prediction       Real
8   150621.345801  152211.77
48   55513.218079   35673.41
14  150369.022458  132602.65
42   74057.015562   71498.49
29  103413.378282  101004.64
44   67844.850378   65200.33
4   173454.059691  166187.94
31   99580.888894   97483.56
13  128147.138396  134307.35
18  130693.433835  124266.90

　

# 生成由State变量衍生的哑变量
dummies=pd.get_dummies(Profit.State)#将离散型特征的每一种取值都看成一种状态
# 将哑变量与原始数据集水平合并
Profit_New=pd.concat([Profit,dummies],axis=1)
# 删除State变量和California变量（因为State变量已被分解为哑变量，New York变量需要作为参照组）
Profit_New.drop(labels=['State','New York'],axis=1,inplace=True)#axis=0代表跨行，axis=1代表跨列,inplace=True,
#不创建新的对象，直接对原始对象进行修改
# 拆分数据集Profit_New
train,test=model_selection.train_test_split(Profit_New,test_size=0.2,random_state=1234)
# 建模
model=sm.formula.ols('Profit~RD_Spend+Administration+Marketing_Spend+Florida+California',data=train).fit()
print('模型的偏回归系数分别为:\n',model.params)

结果：
模型的偏回归系数分别为:
 Intercept          58068.048193
RD_Spend               0.803487
Administration        -0.057792
Marketing_Spend        0.013779
Florida             1440.862734
California           513.468310
dtype: float64

　求相关系数

income.Salary.corr(income.YearsExperience)#相关系数
结果：0.9782416184887598

Profit.corrwith(Profit['Profit'])
结果：
RD_Spend           0.978437
Administration     0.205841
Marketing_Spend    0.739307
Profit             1.000000
dtype: float64

假设检验

目的：验证想法是否准确

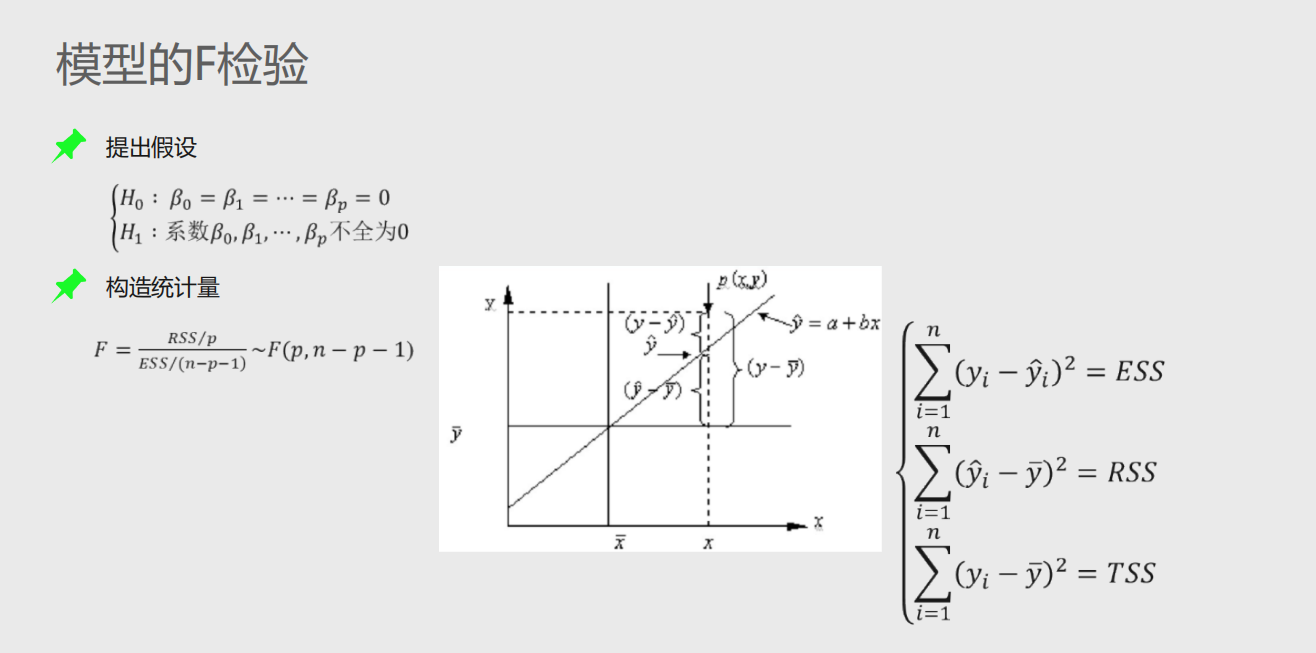
模型的F检验：检验模型的合理性

1、提出问题的原假设和备择假设

2、在原假设的条件下，构造统计量F

3、根据样本信息，计算统计量的值

4、对比统计量的值和理论F分布的值，当统计量值超过理论值时，拒绝原假设，否则接受原假设

 

 

# 导入第三方模块
import numpy as np
# 计算建模数据中因变量的均值
ybar=train.Profit.mean()
# 统计变量个数和观测个数
p=model.df_model
n=train.shape[0]
# 计算回归离差平方和
RSS=np.sum((model.fittedvalues-ybar)**2)
# 计算误差平方和
ESS=np.sum(model.resid**2)
# 计算F统计量的值
F=(RSS/p)/(ESS/(n-p-1))
print('F统计量的值：',F)
# 导入模块
from scipy.stats import f
# 计算F分布的理论值
F_Theroy=f.ppf(q=0.95,dfn=p,dfd=n-p-1)
print('F分布的理论值为：',F_Theroy)

结果：
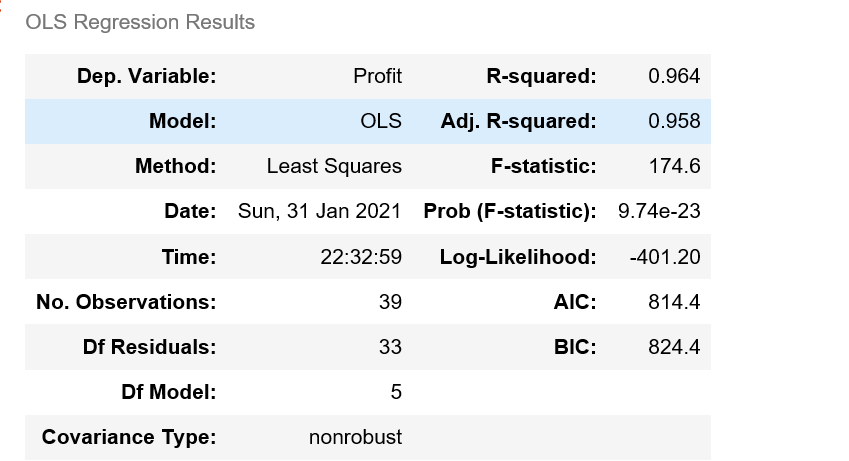
F统计量的值： 174.63721716844674
F分布的理论值为： 2.502635007415366

计算出来的F统计量值174.64远远大于F分布的理论值2.50，所以应当拒绝原假设，即认为多元线性回归模型是显著的，也就是说回归模型的偏回归系数都不全为0。

　　

参数的t检验 

 

 

model.summary()