极限、连续相关
一、极限概念
1、极限定义
定义1:$$\lim_{n \to + \infty}x_n=A$$
- \(\forall_\epsilon>0,\exists_\varepsilon\)正整数N,当 n > N 时,有 \(| x_n-A|< \varepsilon\)。
- 若 \(x_n\)存在极限(有限数),又称\(\{x_n\}\)收敛,否则称\(\{x_n\}\)发散。
定义2:$$\lim_{x \to \infty}f(x)=A$$
- $\forall_\epsilon>0,\exists $ 正整数X,当 |x| > X 时,有 \(| f(x)-A|<\varepsilon\)。
- 类似可定义:
定义3:$$\lim_{x \to x_0}f(x)=A$$
- \(\forall_\epsilon>0,\exists_\varepsilon\)正整数 \(\delta\),当 $ 0< |x-x_0|< \delta$ 时,有 \(| f(x)-A|<\varepsilon\)。
- 类似可定义f(x)当\(x \to x_0\) 时右极限与左极限:
2、极限的基本性质
(1)数列极限的基本性质
定理1:(极限的不等式性质),设
- 若 a > b,则\(\exists N\),当 n > N 时,\(x_n > y_n\);
- 若 n > N 时,\(x_n \geq y_n\),则 \(a \geq b\)。
定理2:(收敛数列的有界性),设 \(x_n\) 收敛,则 \(x_n\) 有界(即 \(\exists\) 常数M > 0,$ |x_n| \leq M $,n = 1,2,...)
(2)函数极限的基本性质
定理3:(极限的不等式性质),设
- 若 A > B,则 \(\exists \delta >0\),当 $ 0< |x-x_0|< \delta $ 时,f(x) > g(x);
- 若 \(f(x) \geq g(x)(0<|x-x_0|<\delta)\) ,则 \(A \geq B\) 。
推论:(极限的保号性),设
- 若 \(A > 0 \implies \exists \delta > 0\),当 \(0<|x-x_0|< \delta\) 时,f(x) > 0;
- 若 \(f(x) \geq 0 (0<|x-x_0|< \delta)\) ,则 \(A \geq 0\) 。
定理4:(存在极限的函数局部有界性),设存在极限
则f(x)在\(x_0\)的某空心领域\(U_0(x_0, \delta)= \{ x| 0<|x-x_0|< \delta \}\) 内有界,即 \(\exists \delta > 0\),M > 0,使得 \(0< |x-x_0|< \delta\) 时,\(|f(x)| \leq M\) 。
(3)两个重要极限
二、极限存在性判别
1、两边夹定理(夹逼定理)
定理5:(数列情形)
若 \(\exists N\) ,当 n > N 时,\(y_n \leq x_n \leq z_n\),且有
定理6:(函数情形)
当 \(x \in U(x_0,r)\) 时,有\(g(x) \leq f(x) \leq h(x)\)成立,并且
(1)三角函数边与角度的关系
- tanx = 对边 / 临边
- sinx = 对边 / 斜边
- cosx = 临边 / 斜边
- cotx = 临边 / 对边
(2)极限案例
注意:由于弧长=圆心角*半径,因此弧\(\mathop{AB}\limits^{\frown}\)长度为x;另外线段OC的长度为cosx,BC线段长度为sinx;由于tanx=对边/临边,因此AD线段长度为tanx。
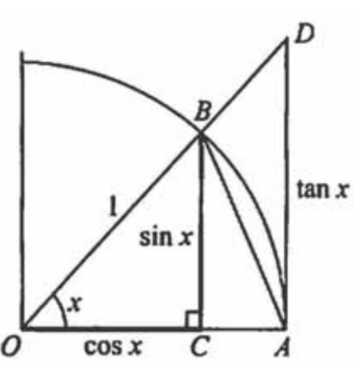
- 因此:sinx:\(\sin x<x<\tan x\),\(x \in U(x_0, \varepsilon)\)
- 从而:\(1 < x/ \sin x < 1/ \cos x\)
- 即:\(\cos x < \sin x /x < 1\)
- 因为:$$\lim_{x \to 0} \cos x = \cos 0 = 1$$
- 从而:$$\lim_{x \to 0} \frac{\sin x}{x}=1$$
- 该式将
三角函数和多项式建立了极限关系
(3)思考平方
同理上式的平方依然是1,即:
2、单调有界数列必有极限(必收敛)
定理7:
-
若数列 \({x_n}\) 单调上升有上界,即\(x_{n+1} \geq x_n\) (n=1,2,...),并存在一个数M,使得对一切的 n 有$ x_n \leq M $,则 \(\{x_n\}\) 收敛,即存在一个数a,使得 $$ \lim_{n \to + \infty}x_n = a $$ 且有 $ x_n \leq a (n =1,2,...)$。
-
若数列 \({x_n}\) 单调下降有下界,即\(x_{n+1} \leq x_n\) (n=1,2,...),并存在一个数m,使得对一切的 n 有$ x_n \geq m $,则 \(\{x_n\}\) 收敛,即存在一个数a,使得 $$ \lim_{n \to + \infty}x_n = a $$ 且有 $ x_n \leq a (n =1,2,...)$。
案例:构造数列\(\{ x_n \}\)
(1)广义二项式定理
二项式定理(英语:binomial theorem),又称牛顿二项式定理,由艾萨克·牛顿于1664年、1665年间提出。该定理给出两个数之和的整数次幂诸如展开为类似项之和的恒等式。二项式定理可以推广到任意实数次幂,即广义二项式定理。
根据定理,可以将x+y的任意次幂展开成和的形式:
每个\(\bigl( \begin{matrix} n \\ k\end{matrix} \bigr)\)为一个称作二项式系数的特定正整数,其等于\(\frac{n!}{k!(n-k)!}\)。
这个公式也称为二项式公式或二项恒等式,使用求和符号,可改写为:
其中
3、单侧极限与双侧极限关系
定理8:
对于分段函数
考察 $$ \lim_{x \to x_0}f(x) $$ 是否存在就要分别求:
三、无穷小及其阶
1、无穷小和无穷大的定义
定义1:在某一极限过程中以零为极限的变量称为无穷小(量)。
- 称 \(x_n\) 为无穷小,若 $$ \lim_{n \to +\infty}x_n=0 $$ 记为 \(x_n= o(1)(n \to + \infty)\)
- 称 \(x \to x_0\) 时 f(x) 为无穷小,若 $$ \lim_{x \to x_0}f(x)=0 $$ 记为 $ f(x)=o(1),x \to x_0 $
定义2:
- 称 $ x_n $ 为
无穷大(量)$$ \lim_{n \to + \infty}x_n= \infty $$
若 $ \forall M > 0 \(,\) \exists $ 自然数N,当 n > N 时,$ |x_n| > M $。 - 称 \(x \to \infty\) 时,f(x)为
无穷大(量)$$ \lim_{x \to \infty}f(x)= \infty$$
若 $ \forall M > 0 \(,\) \exists X > 0$,当 $ |x| > X $ 时,$ |f(x)| > M $。 - 称 $ x \to x_0 $ 时 f(x) 为
无穷大(量)$$ \lim_{x \to x_0}f(x) = \infty$$
若 $ \forall M > 0 \(,\) \exists \delta > 0$ ,当 \(0<|x-x_0|< \delta\) 时,\(|f(x)|> M\)
2、无穷小与无穷大,无穷小与极限的关系
在同一个极限过程中,
\(
\bigg\{ \begin{matrix}
f(x)为无穷小,f(x) \neq0,则 \frac{1}{f(x)}为无穷大 \\
f(x)为无穷大,则 \frac{1}{f(x)}为无穷小
\end{matrix}
\)
3、无穷小阶概念
定义3:设在同一个极限过程中,$ \alpha(x), \beta(x)$ 为无穷小且存在极限 $$ \lim \frac{\alpha(x)}{\beta(x)}=l $$
- 若 $ l \neq 0 $,称 $ \alpha(x), \beta(x) $ 在该极限过程中为
同阶无穷小; - 若 $ l = 1 $,称 $ \alpha(x), \beta(x) $ 在该极限过程中为
等阶无穷小,记为 $ \alpha(x) $ ~ $ \beta(x) $ (极限过程); - 若 $ l = 0 \(,称在该极限过程中\) \alpha(x) 是 \beta(x) $ 的
高阶无穷小,记为 $ \alpha(x) = o( \beta(x)) $ (极限过程).- 若 $$ \lim \frac{\alpha(x)}{\beta(x)}= \infty $$ 称 \(\beta(x) 是 \alpha(x)\) 的高阶无穷小。
- 若 $$ \lim \frac{\alpha(x)}{\beta(x)} 不存在(不为 \infty)$$ 称 \(\alpha(x),\beta(x)\) 不可比较。
定义4:设在同一个极限过程中 $ \alpha(x), \beta(x)$ 为无穷小,以$ \alpha(x) $ 为基本无穷小。
- 若$$ \lim \frac{\beta(x)}{\alpha^k(x)}=l \neq 0 $$ 即 \(\beta(x) 与 \alpha^k(x)\) 为同阶无穷小,称 \(\beta(x) 是 \alpha(x)\) 的 k 阶无穷小。
- 特别是,若 $$ \lim_{x \to x_0} \beta(x)=0,又存在 \lim_{x \to x_0} \frac{\beta(x)}{(x-x_0)^k}$$ 即 \(\beta(x) 与 (x-x_0)^k\) 为同阶无穷小,称 $\beta(x) 是 x-x_0 $ 的 k 阶无穷小。
无穷小阶特性:
- 无穷小比较中的 $ \alpha, \beta$ 必须是在自变量相同变化趋势下的无穷小量;
- 无穷小的比较是定性的,即只有阶的高低之别,无数量上的关系;
- 不是任何无穷小量都可以比较其阶的高低。
4、重要的等价无穷小
在 x ——> 0时:
5、等价无穷小的重要性质
- $ \alpha(x) $ ~ $ \beta(x) \(,\) \beta(x) $ ~ $ \gamma(x) (x \to a) \implies \alpha(x) $ ~ $ \gamma(x)(x \to a) $.
- $ \alpha(x) $ ~ $ \beta(x) (x \to a) \iff \alpha(x)= \beta(x) + o(\beta(x))(x \to a)$.
- 求极限过程中,积、商可用等价无穷小因子替换;
有限个无穷小的和依然是无穷小;- 有界函数与无穷小的乘积为无穷小;
- 无穷个无穷小的和或积不一定为无穷小。
6、确定无穷小阶的方法
四、求极限的方法
1、利用极限的四则运算与幂指数运算法则求极限
(1)极限的四则运算法则
- 设 $$ \lim_{x \to a}f(x)=A, \lim_{x \to a}g(x)=B $$
则 $$ \lim_{x \to a}[f(x) \pm g(x)]=A \pm B, \lim_{x \to a}[f(x) \cdot g(x)]$$
- 各自极限存在才能运用极限四则运算;
- 函数的和、差、积、商的极限存在不能得出各自极限存在。
(2)有界函数与无穷小的乘积为无穷小
设 $$ \lim_{x \to a}f(x)=0$$,当 $ 0<|x-a|< \delta $ 时 g(x) 有界,则 $$ \lim_{x \to a}[f(x)g(x)]=0 $$
(3)无穷大与无穷大(非零有界函数)的积为无穷大
(4)有界函数与无穷大之和为无穷大
(5)有界函数的无穷大次幂和无穷大次幂的有界函数次幂(未定性)
(6)无穷小的有界函数次幂(未定性)
2、利用函数的连续性求极限
- 设 \(f(x)\) 在 \(x = a\) 连续,按定义则有 $$ \lim_{x \to a}f(x)=f(a). $$ 因此若不用定义可判断函数连续时,那么对连续函数求极限就是用
代入法求函数值。 - 一切初等函数在其定义域区间上连续,因此,若 \(f(x)\) 是初等函数,a 属于其定义域区间,则 $$ \lim_{x \to a}f(x)=f(a). $$
-
\[\text 设 \lim_{x \to a}g(x)=A, \]
- 若补充定义 \(g(a)=A\),则 $g(x) 在 x=a $ 连续;
- 若又有 \(y=f(u) 在 u=A处连续\),则由符合函数的连续性得到 $$ \lim_{x \to a}f(g(x))=f(\lim_{x \to a}g(x))=f(A). $$
3、利用变量替换法与两个重要极限求极限
通过变量替换,把求某个极限转化为求另一个极限。
-
\[设 \lim_{x \to + \infty}\varphi(x) = + \infty, \lim_{u \to + \infty}f(u)=A, 则 \]
-
\[设 \lim_{x \to x_0}\varphi(x)=u_0,f(u)在 u_0连续,则 \]
4、利用等价无穷小因子替换求极限
若 \(x \to a\) 时,无穷小 $\alpha(x) $ ~ \(\alpha^*(x)\),$\beta(x) $ ~ \(\beta^*(x)\) 则
等式两边其中之一极限存在或为\(\infty\),则另一也是且相等。
结论表明:在求极限过程中等价无穷小因子可以替换。
利用等价无穷小因子替换求极限注意事项:
- 只要求在求极限的乘除运算中使用等价无穷小因子替换,不要在求极限的加减运算中使用,在加减法中等价无穷小的替换是有条件的
- 要熟练运用3-4中重要等价无穷小。
5、利用洛必达法则求未定式的极限
求 \(\frac{0}{0}\) 或 \(\frac{\infty}{\infty}\) 型未定式更常用的方法是洛必达法则
(1)定理
设
(2)使用条件
1)$x \to x_0 或 x \to \infty ,f(x)、g(x) $ 都趋于零或都趋于无穷大;
2)$$ f(x)、g(x) 在 x_0 的去心邻域可导,且 g'(x) \neq 0 ;$$
3)$$ \lim_{x \to x_0(x \to \infty)} \frac{f'(x)}{g'(x)} 存在或为无穷大。 $$
(3)应用法则注意事项
-
\[若 \lim_{x \to a} \frac{f'(x)}{g'(x)} 不存在也不为无穷大,不能说明 \lim_{x \to a}\frac{f(x)}{g(x)} 不存在。 \]
- 要验证应用法则的条件;
-
\[若 \lim_{x \to a} \frac{f'(x)}{g'(x)} 还是 \frac{0}{0}型或 \frac{\infty}{infty} \text型 \]
则可连续用洛必达法则,只要符合条件,可一直用到求出极限为止;
4. 其他类型的未定式 $( 0* \infty , \infty-\infty, 0^0, 1^{\infty}, \infty^0等) $ 先化成 $ \frac{0}{0} 或 \frac{\infty}{\infty}型 $,再用洛必达法则;
5. 使用洛必达法则也要用一些技巧,如结合应用变量替换、等价无穷小因子替换、极限的四则运算法则、有确定非零极限的因子应先求出等。
6、分别求左右极限求得函数极限
求分段函数在连接点处的极限,或函数表达式中含有左、右极限不相等的项(如 $x \to 0 时,e^{\frac{1}{x}},arctan \frac{1}{x} 时 $),要分别求左、右极限求得函数极限。
7、利用函数极限求数列极限
即若 \(y_n\) 可看成某函数在一串点 \(x_n\) 上的函数值:$$ y_n=f(x_n),而 x_n \to + \infty,又知 \lim_{x \to + \infty}f(x)=A ,则 \lim_{n \to + \infty}y_n=A.$$
注意1:$$ 若 \lim_{x \to + \infty}f(x)=A,y_n=f(n),则 \lim_{n \to + \infty}y_n=A. $$
注意2:求数列极限转化为求函数极限的主要目的是为了用洛必达法则。
8、夹逼法求极限
用夹逼定理求极限,就是要将数列 \(\{x_n\}\) 放大与缩小成:\(z_n \leq x_n \leq y_n.\)
(1)简单放大缩小手段
常见手段如下:
- n 个数之和不超过最大数乘 n,不小于最小数乘 n;
- 分子与分母同为正数,把分母放大则分数值缩小;
- 若干正数的乘积中,把小于1的因子略去则乘积放大,把大于1的因子略去则乘积缩小等。
(2)利用极限不等式性质进行放大或缩小
例题:$$ 求数列极限: \lim_{n \to +\infty} \frac{3^n}{n!}; $$
解:由于
(3)对积分的极限可利用积分的性质进行放大或缩小
例题:设$ f(x) $ 在 [0,1] 上连续,求 $$ \lim_{n \to +\infty} \int_0^1 {x^n}f(x)dx $$
解:因为
且连续函数$ |f(x)| 在 [0,1] $ 存在最大值记为 M,于是
9、递归数列极限的求法
数列 \(\{ a_n\}\) 如果满足递归方程 \(a_{n+1}=f(a_n)(n=1,2,3,...),f\) 是已知的一元连续函数,则称 \(\{ a_n\}\) 为递归数列。
由递归方程可知,由 \(a_1\) 可求出 \(a_2\) ,由 \(a_2\) 可求 \(a_3\) ,以此类推可求出任意项 \(a_n\) ,因此求递归数列极限的方法很重要:
- 方法一:先验证递归数列 \(a_n\) 收敛(常用单调有界数列必收敛定理),然后设 $$ \lim_{n \to + \infty}x_n=A ,$$
再对递归方程 \(a_{n+1}=f(a_n) 取极限得 A=f(A)\) ,最后解出 A 即可。 - 方法二:先设 $$ \lim_{n \to + \infty}x_n=A ,$$ 对递归方程取极限后解得A,再用某种方法证明 $$ \lim_{n \to +\infty}x_n=A $$。
10、利用定积分求某些 n 项和式的极限
11、利用泰勒公式求未定式的极限
12、利用导数定义求极限
五、函数的连续性及其判断
1、连续性概念
定义:
- 若 $$ \lim_{x \to x_0}f(x)=f(x_0) $$,称 \(f(x)\) 在 \(x_0\) 连续。
- 若 $$ \lim_{x \to x_0+}f(x)=f(x_0)( \lim_{x \to x_0-}f(x)=f(x_0) ) $$,称 \(f(x)\) 在 $ x=x_0$ 连续。
- 若 \(f(x)\) 在 (a,b)内任一点均连续,称 \(f(x)\) 在 (a,b)连续。
- 若 \(f(x)\) 在 (a,b)连续,在 \(x=a\) 右连续,在 \(x=b\) 左连续,称 \(f(x) 在 [a,b] 上连续\) 。
定理(单双侧连续性的关系):$f(x) 在 x_0 连续 \iff f(x) 在 x_0 $ 既左连续又右连续。
2、间断点的定义与分类
设 \(f(x)\) 在 \(x_0\) 的空心邻域或单侧空心邻域有定义,\(x=x_0\) 不是 \(f(x)\) 的连续点,则称 \(x_0\) 是 \(f(x)\) 的间断点。
设 \(f(x)\) 在 \(x_0\) 的空心邻域有定义,间断点 \(x_0\) 的类型。
第一类间断点$ \stackrel{\triangle}{=} f(x_0+0) 与 f(x_0-0) $ 均存在。(左、右极限均存在)- 可去间断点:$ f(x_0+0) = f(x_0-0) \neq f(x_0) 或 f(x_0) $ 无定义。(左极限等于右极限)
- 跳跃间断点:$ f(x_0+0) \neq f(x_0-0) $ 。(左极限不等于右极限)
第二类间断点$ \stackrel{\triangle}{=} f(x_0+0) 与 f(x_0-0) $ 中至少有一个不存在。- 无穷间断点:$ f(x_0+0) 与 f(x_0-0) $ 中至少有一个为 \(\infty\) 。
3、判断函数的连续性和间断点的类型
(1)判断函数连续性的方法
1)若是初等函数,则在它的定义域区间上处处连续;
2)用连续性运算法则;
3)分别判断左右连续性或按定义来判断。
(2)定理(连续性运算法则)
1)连续性的四则运算法则:设 \(f(x),g(x) 在 x_0 连续,则f(x) \pm g(x),f(x)*g(x),f(x)/g(x)(g(x_0) \neq 0) 在 x_0 也连续。\)
2)复合函数的连续性:设 $ u=\varphi(x) 在 x=x_0 连续,y=f(u) 在 u=u_0(u_0= \varphi(x_0)) 连续,则 f(\varphi(x)) 在 x=x_0 连续。 $
3)反函数的连续性:设 $ y=f(x) 在区间 I_x 上单调且连续,则反函数 x=\varphi(y) 也在对应的区间 I_y= {y|y=f(x),x \in I_x } 上连续且有相同的单调性。 $
4、连续函数的性质
(1)连续函数的局部性质
设 \(f(x) 在 x=x_0 连续,f(x_0) > 0,则 \exists \delta >0,当 |x-x_0|< \delta 时,f(x)>0。\)
(2)连续函数介值定理(中间值定理)
设 $f(x) 在 [a,b] 上连续,f(x) \neq f(b),则对 f(a) 与 f(b) 之间的任何数 \eta,必 \exists c(a<c<b),使得 f(c)=\eta。 $
连续函数零点存在性定理(推论):设 $ f(x)在 [a,b] 上连续,又 f(a) 与 f(b) 异号,则 \exists c \in (a,b),使得 f(c)=0(c 称为 f(x)的零点)。 $
(3)有界闭区间上连续函数的有界性
设 $ f(x) 在 [a,b] 上连续,则 f(x) 在 [a,b] 上有界,即存在常数 M>0,使得 |f(x)| \leq M (x \in [a,b]) $
即 f(x)在 [a,b] 连续则它在 [a,b] 必有界。
(4)有界闭区间上连续函数存在最大、最小值
设 $ f(x) 在 [a,b] 上连续,则在 [a,b] 上必存在x_1,x_2,$ 使得
即 $ f(x) 在 [a,b]上连续,则 f(x) 在 [a,b] 上有最大值、最小值。 $
5、方程式根的存在性与根的估计
连续函数介值定理的推论————连续函数零点存在性定理,
连续函数零点存在性定理(推论):设 $ f(x)在 [a,b] 上连续,又 f(a) 与 f(b) 异号,则 \exists c \in (a,b),使得 f(c)=0(c 称为 f(x)的零点)。 $
可用于证明方程 \(f(x)=0\) 存在根,并给出根的大小估计。
(1)例题
例:证明 $ cosx - \frac{1}{x} = 0 $ 有无穷多个正根,并指明这一事实的几何意义。
解:令 $ f(x)=cosx- \frac{1}{x}, a_n=2n\pi, b_n=(2n+1)\pi, 则 $
由 $ f(a_n)= 1 - \frac{1}{2n\pi} > 0,\quad f(b_n)=-1- \frac{1}{(2n+1)\pi} < 0 \implies $
几何意义:令 $ f(x)=cosx- \frac{1}{x} , f(x)=0 有无穷多个正根的几何意义是曲线 y=f(x) 与正 x 轴有无穷多个交点。 $



 浙公网安备 33010602011771号
浙公网安备 33010602011771号