树上数据结构
目录
树上问题
树链剖分学习笔记
重链剖分
对树进行重链优先搜索,暴力求一条路径的复杂度为logn
模板
int siz[MAXN],f[MAXN],hson[MAXN],deep[MAXN],top[MAXN],dfn[MAXN],rdfn[MAXN],rak[MAXN],cnt;
void tree_build(int u,int fa) {//重链优先搜索
siz[u]=1;
f[u]=fa;
hson[u]=0;
for(auto &v:adj[u]) {
if(v==fa) continue;
deep[v]=deep[u]+1;
tree_build(v,u);
siz[u]+=siz[v];
if(hson[u]==0||siz[v]>siz[hson[u]]) hson[u]=v;
}
}
void tree_decom(int u,int t) {//dfn序
top[u]=t;
cnt++;
dfn[u]=cnt;
rak[cnt]=u;
if(hson[u]!=0) {
tree_decom(hson[u],t);
for(auto &v:adj[u]) {
if(hson[u]!=v&&v!=f[u]) tree_decom(v,v);
}
}
rdfn[u]=cnt;
}
求LCA
int getLCA(int u,int v) {
while(top[v]!=top[u]) {
if(deep[top[u]]>deep[top[v]]) u=f[top[u]];
else v=f[top[v]];
}
return deep[u]>deep[v]?v:u;
}
模板题1 洛谷模板

代码
while(m--) {
int op;
cin>>op;
if(op==1) {
int u,v,w;
cin>>u>>v>>w;
while(top[v]!=top[u]) {
if(deep[top[u]]>deep[top[v]]) {
modify(1,1,n,dfn[top[u]],dfn[u],w);
u=f[top[u]];
} else {
modify(1,1,n,dfn[top[v]],dfn[v],w);
v=f[top[v]];
}
}
if(dfn[v]<dfn[u]) swap(u,v);
modify(1,1,n,dfn[u],dfn[v],w);
} else if(op==2) {
int u,v;
cin>>u>>v;
int ans=0;
while(top[v]!=top[u]) {
if(deep[top[u]]>deep[top[v]]) {
ans+=query(1,1,n,dfn[top[u]],dfn[u]).sum;
u=f[top[u]];
} else {
ans+=query(1,1,n,dfn[top[v]],dfn[v]).sum;
v=f[top[v]];
}
}
if(dfn[v]<dfn[u]) swap(u,v);
ans+=query(1,1,n,dfn[u],dfn[v]).sum;
cout<<ans%p<<"\n";
} else if(op==3) {
int u,w;
cin>>u>>w;
modify(1,1,n,dfn[u],rdfn[u],w);
} else if(op==4) {
int u;
cin>>u;
int ans=query(1,1,n,dfn[u],rdfn[u]).sum;
cout<<ans%p<<"\n";
}
}
模板题2 Omsk Metro (hard version)

思路

代码
//线段树
Info operator + (const Info &a,const Info &b){
Info c;
c.sum=a.sum+b.sum;
c.lmin=min(a.lmin,a.sum+b.lmin);
c.lmax=max(a.lmax,a.sum+b.lmax);
c.rmin=min(b.rmin,b.sum+a.rmin);
c.rmax=max(b.rmax,b.sum+a.rmax);
c.min=min({a.min,a.rmin+b.lmin,b.min});
c.max=max({a.max,a.rmax+b.lmax,b.max});
return c ;
}
//main函数
for(auto it:que){
int u=it.first.first;
int v=it.first.second;
int value=it.second;
Info answer;//ans是最后的信息合并
if(deep[u]<deep[v]) swap(u,v);
Info left,right;
while(top[u]!=top[v]){//跳重链
if(deep[top[u]]>deep[top[v]]){
left=query(1,min(dfn[top[u]],dfn[u]),max(dfn[top[u]],dfn[u]))+left;
u=f[top[u]];
}
else{
right=query(1,min(dfn[top[v]],dfn[v]),max(dfn[top[v]],dfn[v]))+right;
v=f[top[v]];
}
}
if(dfn[u]<=dfn[v])
right=query(1,min(dfn[u],dfn[v]),max(dfn[u],dfn[v]))+right;
else
left=query(1,min(dfn[u],dfn[v]),max(dfn[u],dfn[v]))+left;
answer = rev(left)+right;
if(value>=answer.min&&value<=answer.max) cout<<"YES\n";
else cout<<"NO\n";
}
长链剖分
树上启发式合并学习笔记
模板
优化合并复杂度的方法
重链剖分
复杂度为logn
void tree_build(int u,int fa){
siz[u]=1;
hson[u]=0;
for(auto &v:adj[u]){
if(v==fa) continue;
dep[v]=dep[u]+1;
tree_build(v,u);
siz[u]+=siz[v];
if(siz[v]>siz[hson[u]])hson[u]=v;
}
}
长链剖分
复杂度为根号n 用于优化树上dp
void tree_build(int u,int fa){
int maxdep=0;
deep[u]=1;
for(auto &v:adj[u]){
if(v==fa) continue;
f[v]=u;
tree_build(v,u);
if(deep[v]>maxdep){
maxdep=deep[v];
lson[u]=v;
}
deep[u]=max(deep[u],deep[v]+1);
}
}
合并信息模板
void calc(int u,int fa,int val) { //统计答案
if(val==1){//表示在增加这个节点时需要增加的操作
}
else{//表示在去掉这个节点时需要消去的操作
}
for(auto &v:adj[u]) {
if(v==fa||v==HH) continue;
calc(v,u,val);
}
}
void dsu(int u,int fa,int op){
for(auto &v:adj[u]){
if(v==fa||v==hson[u]) continue;
dsu(v,u,0);
}
if(hson[u]){
dsu(hson[u],u,1),
HH=hson[u];
}
calc(u,fa,1);
/*在这里对答案进行统计 一般每个dsu(u)的答案就是该节点的答案
*/
HH=0;
if(!op){calc(u,fa,-1);
}
}
题目选
题1 Lomsat gelral
寻找子树最大颜色的和
void calc(int u,int fa,int val) { //统计答案
if(val==1){
cntc[c[u]]++;//增加颜色操作
if(cntc[c[u]]>ma){
ma=cntc[c[u]];
res=c[u];
}
else if(cntc[c[u]]==ma)
res+=c[u];
}
}
else{
cntc[c[u]]--;//减少颜色
if(cntc[c[u]]>ma){
ma=cntc[c[u]];
res=c[u];
}
else if(cntc[c[u]]==ma){
res+=c[u];
}
}
//增加或者减少后,统计新的值
for(auto &v:adj[u]) {
if(v==fa||v==HH) continue;
calc(v,u,val);
}
}
void dsu(int u,int fa,int op) { //op=1 传递 否则保留
for(auto &v:adj[u]) {
if(v==fa||v==hson[u]) continue;
dsu(v,u,0);//先遍历轻儿子
}
if(hson[u]) dsu(hson[u],u,1),HH=hson[u];
calc(u,fa,1);
ans[u]=res; //统计每个点答案
HH=0;
if(!op) calc(u,fa,-1),res=ma=0;//表示不用传递,要把res清空
}
题2 Blood Cousins Return
寻找子树每一层不同颜色的个数
用set去统计对于每个dsu到的点的节点信息 set表示离根节点距离的名字

void calc(int u,int fa,int val) { //统计答案
if(val==1){
v[dep[u]].insert(s[u]);//加入节点
}
else{
v[dep[u]].erase(s[u]);
}
for(auto &v:adj[u]) {
if(v==fa||v==HH) continue;
calc(v,u,val);
}
}
void dsu(int u,int fa,int op){
for(auto &v:adj[u]){
if(v==fa||v==hson[u]) continue;
dsu(v,u,0);
}
if(hson[u]){
dsu(hson[u],u,1),
HH=hson[u];
}
calc(u,fa,1);
for(auto &it:Q[u]){
int h=it[0],id=it[1];
ans[id]=v[dep[u]+h].size();
}
HH=0;
if(!op){calc(u,fa,-1);
}
}
题3 彩色的树
处理子树内某个深度差内的节点信息
考虑把信息全塞set里面 在从下往上dsu的时候,传递的同时删除深度越出的节点
void del(int x){//删除过多节点
if(x>n) return;
while(!deps[x].empty()){
auto it=deps[x].begin();
if(cntc[*it]==1) res--;
cntc[*it]--;
deps[x].erase(it);
}
}
void calc(int u,int fa,int val,int lim,int Son) { //统计答案
if(deep[u]>lim) return;
if(val==1){
if(cntc[c[u]]==0){
res++;
} deps[deep[u]].insert(c[u]);
}
else {
if(cntc[c[u]]==1){
res--;
}
auto it=deps[deep[u]].find(c[u]);
deps[deep[u]].erase(it);
}
cntc[c[u]]+=val;
for(auto &v:adj[u]) {
if(v==fa||(val==1&&v==Son)) continue;
calc(v,u,val,lim,Son);
}
}
void dsu(int u,int fa,int op) { //op=1 传递 否则保留
for(auto &v:adj[u]) {
if(v==fa||v==hson[v]) continue;
dsu(v,u,0);//先遍历轻儿子
}
if(hson[u]!=-1) dsu(hson[u],u,1);
calc(u,fa,1,deep[u]+k,hson[u]);
ans[u]=res;
if(!op) calc(u,fa,-1,deep[u]+k,hson[u]);//表示不用传递
else{ del(deep[u]+k);
}
}
点分治
模板
void dfs(int x, int fa, ll sum, ll mx){
ll s = sum + a[x];
ll mm = max(mx, a[x]);
o.push_back({mm, s});
all1.push_back({mm, s});
vx.push_back(s);
for(auto v : adj[x]){
if(v == fa || del[v]) continue;
dfs(v, x, s, mm);
}
}
void calc(int x){
//统计答案
}
void getroot(int x, int fa){
sz[x] = 1;
int max_part = 0;
for(auto &v : adj[x]){
if(v == fa || del[v]) continue;
getroot(v, x);
sz[x] += sz[v];
max_part = max(max_part, sz[v]);
}
max_part = max(max_part, sum - sz[x]);
if(max_part < tmp){
tmp = max_part;
root = x;
}
}
void divide(int x){
calc(x);
del[x] = 1;
for(auto &v : adj[x]){
if(del[v]) continue;
tmp = sum = sz[v];
getroot(v, 0);
divide(root);
}
}
题目选
题1 聪聪可可
代码
#include<bits/stdc++.h>
#define close std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
using namespace std;
typedef long long ll;
const ll MAXN = 3e5+7;
const ll mod = 1e9+7;
const ll inf = 0x3f3f3f3f;
int tmp,sum,root,ans=0,del[MAXN],sz[MAXN];
int f[3];
vector<pair<int,int> > adj[MAXN];
void dfs(int u, int fa, ll D) {
for(auto it : adj[u]) {
int v=it.first;
int w=it.second;
if(v == fa || del[v]) continue;
f[(D+w)%3]++;
dfs(v, u, w+D);
}
}
int calc(int u,int D) {
//统计答案
memset(f,0,sizeof(f));
f[D%3]++;
dfs(u,0,D);
return f[0]*f[0]+f[1]*f[2]*2;
}
void getroot(int x, int fa) {
sz[x] = 1;
int max_part = 0;
for(auto &it : adj[x]) {
int v=it.first;
int w=it.second;
if(v == fa || del[v]) continue;
getroot(v, x);
sz[x] += sz[v];
max_part = max(max_part, sz[v]);
}
max_part = max(max_part, sum - sz[x]);
if(max_part < tmp) {
tmp = max_part;
root = x;
}
}
void divide(int x) {
ans+=calc(x,0);
del[x] = 1;
for(auto &it : adj[x]) {
int v=it.first;
int w=it.second;
if(del[v]) continue;
ans-=calc(v,w);
tmp = sum = sz[v];
getroot(v, 0);
divide(root);
}
}
void solve() {
int n;
cin>>n;
for(int i=1; i<n; i++) {
int u,v,w;
cin>>u>>v>>w;
adj[u].push_back({v,w});
adj[v].push_back({u,w});
}
tmp=sum=n;
getroot(1,0);
getroot(root,0);
divide(root);
// ans+=n;
int fm=n*n;
int k=__gcd(ans,fm);
cout<<ans/k<<"/"<<fm/k;
}
signed main() {
solve();
}
虚树
在问题询问很少但是树很大的情况下
可以考虑建虚树,保留关键点和关键点的lca
模板
vector<int> G[MAXN];
vector<pair<int,int> > Q[MAXN];
int par[MAXN][20],dep[MAXN];
//par[u][i]代表点u的祖先中 深度为max(1,dep[u]-2^i)是谁
void dfs(int u,int fa) {
dep[u]=dep[fa]+1;
par[u][0]=fa;
for(int i=1; i<20; ++i) {
par[u][i]=par[par[u][i-1]][i-1];
}
for(auto &v:G[u]) {
if(v==fa) continue;
dfs(v,u);
}
}
void dfs2(int u,int fa) {
d[u]=d[fa]+1;
f[u]=fa;
for(auto &v:vg[u]) {
if(v==fa) continue;
dfs2(v,u);
}
}
int getLCA(int u,int v) {
if(dep[u]<dep[v]) swap(u,v);
for(int i=19; i>=0; --i) {
if(dep[par[u][i]]>=dep[v]) u=par[u][i];
}
if(u==v) return u;
for(int i=19; i>=0; i--) {
if(par[u][i]!=par[v][i]) {
u=par[u][i];
v=par[v][i];
}
}
return par[u][0];
}
void init(int u,int fa) {
in[u]=++tim;
for(auto it:adj[u]) {
int v=it.first,w=it.second;
if(v==fa) continue;
init(v,u);
}
out[u]=tim;
}
int isp(int u, int v) {
return in[u] <= in[v] && out[v] <= out[u];
}
bool cmp(int u, int v) {
return in[u] < in[v];
}
void build(vector<int>&node) {
sort(node.begin(), node.end(), cmp);
set<int>node_st;
for (int x : node)node_st.insert(x);
for (int i = 1; i < node.size(); i++)node_st.insert(getLCA(node[i - 1], node[i]));
node.clear();
for (int x : node_st)node.push_back(x);
sort(node.begin(), node.end(), cmp);
vector<int> st;
for (int v : node) {
while (!st.empty() && !isp(st.back(), v))
st.pop_back();
if (!st.empty())
vg[st.back()].push_back({ v ,mi[v] });
st.push_back(v);
}
}
//node.push_back(1)
//build(node);
题1 Master of Data Structure
-
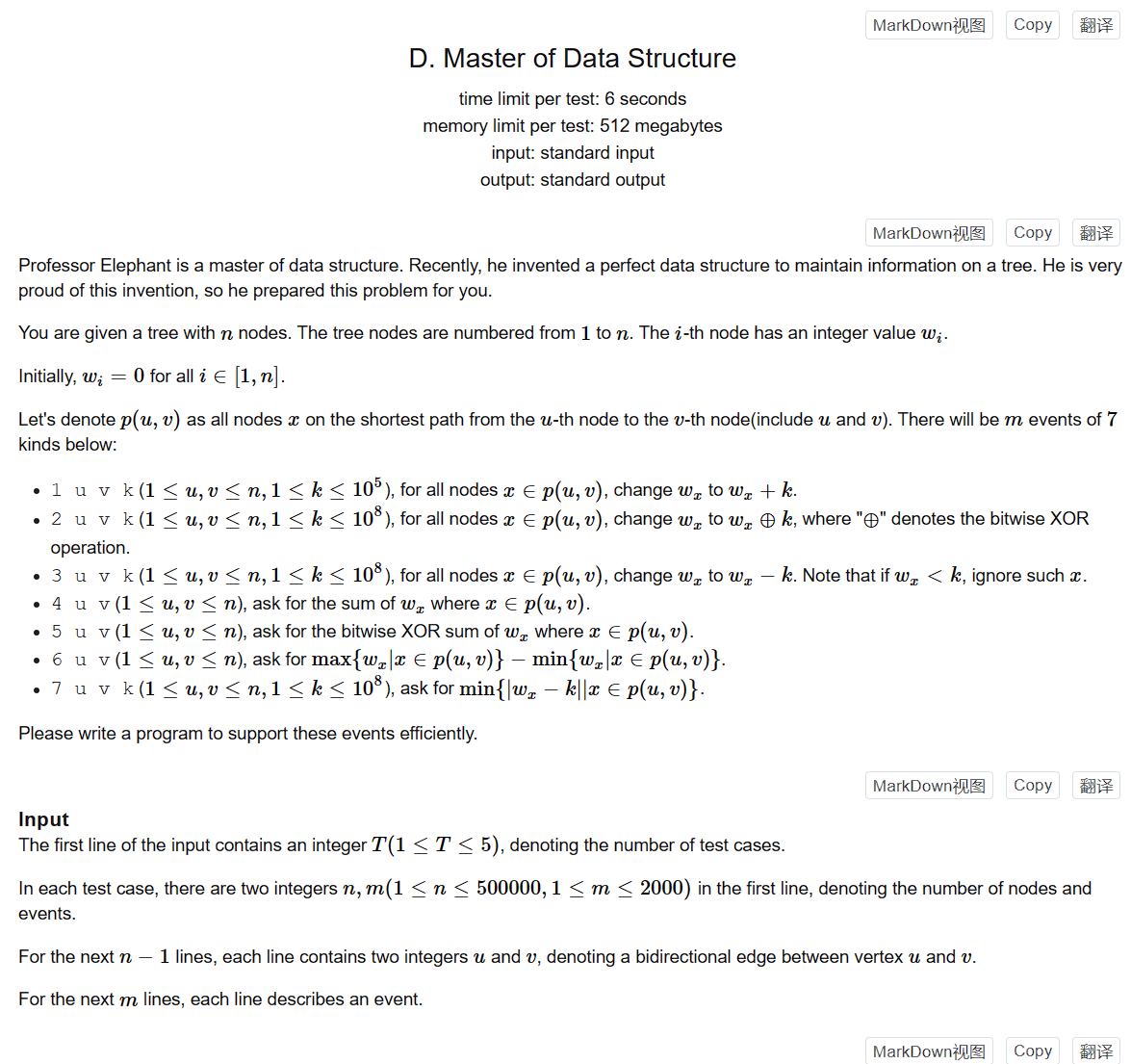
有7种操作,说来惭愧,场上我真准备硬做。。树剖都上了,现在想想真nt
只有2000次询问,因此点的数量最多有4000个点,即使我对这每个询问跑O(n)都不会超时
所以对这个询问维护一个虚树,a数组记真实的点的值 w数组记这个a点向上连的边的值 然后像树剖跳链一样往上跳,维护就行了 在67操作的时候 如果向上的边上没有点记得别算上
vector<array<int,4> > Q; vector<int> adj[MAXN],vg[MAXN]; int par[MAXN][20],dep[MAXN]; int f[MAXN]; int w[MAXN];//u点向上的权值 int a[MAXN]; int d[MAXN]; //par[u][i]代表点u的祖先中 深度为max(1,dep[u]-2^i)是谁 int in[MAXN],out[MAXN],tim=0; void dfs(int u,int fa) { dep[u]=dep[fa]+1; par[u][0]=fa; for(int i=1; i<20; ++i) { par[u][i]=par[par[u][i-1]][i-1]; } for(auto &v:adj[u]) { if(v==fa) continue; dfs(v,u); } } int getLCA(int u,int v) { if(dep[u]<dep[v]) swap(u,v); for(int i=19; i>=0; --i) { if(dep[par[u][i]]>=dep[v]) u=par[u][i]; } if(u==v) return u; for(int i=19; i>=0; i--) { if(par[u][i]!=par[v][i]) { u=par[u][i]; v=par[v][i]; } } return par[u][0]; } void init(int u,int fa) { in[u]=++tim; for(auto v:adj[u]) { if(v==fa) continue; init(v,u); } out[u]=tim; } int isp(int u, int v) { return in[u] <= in[v] && out[v] <= out[u]; } bool cmp(int u, int v) { return in[u] < in[v]; } void build(vector<int>&node) { sort(node.begin(), node.end(), cmp); set<int>node_st; for (int x : node)node_st.insert(x); for (int i = 1; i < node.size(); i++)node_st.insert(getLCA(node[i - 1], node[i])); node.clear(); for (int x : node_st)node.push_back(x); sort(node.begin(), node.end(), cmp); vector<int> st; for (int v : node) { while (!st.empty() && !isp(st.back(), v)) st.pop_back(); if (!st.empty()) { vg[st.back()].push_back(v); } st.push_back(v); } } void dfs2(int u,int fa) { d[u]=d[fa]+1; f[u]=fa; for(auto &v:vg[u]) { if(v==fa) continue; dfs2(v,u); } } //node.push_back(1) //build(node); void work(int u,int v,int k,int op) { int ans=0; if(op==1) { while(u!=v) { assert(u&&v); if(d[u]>d[v]) { a[u]+=k; w[u]+=k; u=f[u]; } else { a[v]+=k; w[v]+=k; v=f[v]; } } a[u]+=k; } else if(op==2) { while(u!=v) { assert(u&&v); if(d[u]>d[v]) { a[u]^=k; w[u]^=k; u=f[u]; } else { a[v]^=k; w[v]^=k; v=f[v]; } } a[u]^=k; } else if(op==3) { while(u!=v) { assert(u&&v); if(d[u]>d[v]) { if(a[u]>=k) a[u]-=k; if(w[u]>=k) w[u]-=k; u=f[u]; } else { if(a[v]>=k) a[v]-=k; if(w[v]>=k) w[v]-=k; v=f[v]; } } if(a[u]>=k) a[u]-=k; } else if(op==4) { while(u!=v) { assert(u&&v); if(d[u]>d[v]) { ans+=(dep[u]-dep[f[u]]-1)*w[u]+a[u]; u=f[u]; } else { ans+=(dep[v]-dep[f[v]]-1)*w[v]+a[v]; v=f[v]; } } ans+=a[u]; cout<<ans<<"\n"; } else if(op==5) { while(u!=v) { assert(u&&v); if(d[u]>d[v]) { ans^=a[u]; if((dep[u]-dep[f[u]]-1)%2==1) ans^=w[u]; u=f[u]; } else { ans^=a[v]; if((dep[v]-dep[f[v]]-1)%2==1) ans^=w[v]; v=f[v]; } } ans^=a[u]; cout<<ans<<"\n"; } else if(op==6) { int mins=a[u],maxs=a[u]; while(u!=v) { assert(u&&v); if(d[u]>d[v]) { mins=min(mins,a[u]); if((dep[u]-dep[f[u]]-1)) mins=min(mins,w[u]); maxs=max(maxs,a[u]); if((dep[u]-dep[f[u]]-1)) maxs=max(maxs,w[u]); u=f[u]; } else { mins=min(mins,a[v]); if((dep[v]-dep[f[v]]-1)) mins=min(mins,w[v]); maxs=max(maxs,a[v]); if((dep[v]-dep[f[v]]-1)) maxs=max(maxs,w[v]); v=f[v]; } } mins=min(mins,a[u]); maxs=max(maxs,a[u]); ans=maxs-mins; cout<<ans<<'\n'; } else if(op==7) { ans=inf; while(u!=v) { assert(u&&v); if(d[u]>d[v]) { ans=min(ans,abs(a[u]-k)); if((dep[u]-dep[f[u]]-1)) ans=min(ans,abs(w[u]-k)); u=f[u]; } else { ans=min(ans,abs(a[v]-k)); if((dep[v]-dep[f[v]]-1)) ans=min(ans,abs(w[v]-k)); v=f[v]; } } ans=min(ans,abs(a[u]-k)); cout<<ans<<"\n"; } } void solve() { int n,q; cin>>n>>q; vector<int> node; Q.clear(); tim=0; for(int i=1; i<=n; i++) { for(int j=0; j<20; j++) par[i][j]=0; adj[i].clear(); vg[i].clear(); a[i]=0; w[i]=0; dep[i]=0; d[i]=0; } for(int i=1; i<n; i++) { int u,v; cin>>u>>v; adj[u].push_back(v); adj[v].push_back(u); } dfs(1,0); init(1,0); set<int> sta; for(int i=1; i<=q; i++) { int op; cin>>op; if(op==1||op==2||op==3||op==7) { int u,v,k; cin>>u>>v>>k; Q.push_back({op,u,v,k}); sta.insert(u); sta.insert(v); } else { int u,v; cin>>u>>v; Q.push_back({op,u,v,0}); sta.insert(u); sta.insert(v); } } sta.insert(1); assert(sta.size() <= 6000); for(auto &it:sta) node.push_back(it); build(node); dfs2(1,0); for(int i=0; i<q; i++) { int op=Q[i][0],u=Q[i][1],v=Q[i][2],k=Q[i][3]; work(u,v,k,op); // cout<<"TEST : \n"; // for(int i=1; i<=n; i++) { // cout<<"a: "<<a[i]<<" w: "<<w[i]<<"\n"; // } } } signed main() { close; int t; cin>>t; while(t--) solve(); }






 浙公网安备 33010602011771号
浙公网安备 33010602011771号