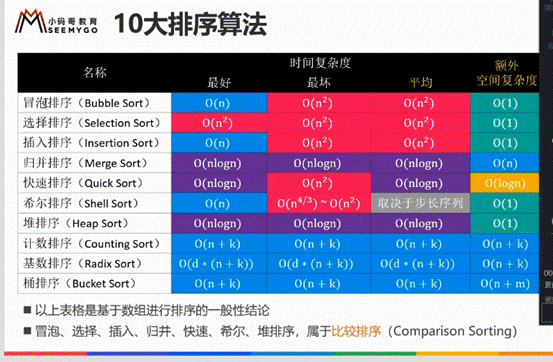
十大排序

十大排序

 

 

使用枚举法思想：

选择排序

简单选择排序实现过程

初始序列 【49 27 65 76 38 13】

第1趟排序结果 13【27 65 76 38 49】

第2趟排序结果 13 27【65 76 38 49】

第3趟排序结果 13 27 38【76 65 49】

第4趟排序结果 13 27 38 49【65 76】

第5趟排序结果 13 27 38 49 65 76

 

实现思想

分为有序区和无序区，在无序区查找值最小的记录并将它与无序区第一个记录做交换

也就是在无序区选择出最小的值，并放到有序区的最后

平均时间性能

O（n^2）

最好最坏的平均时间复杂度也是O（n^2）

平均性能优于冒泡

 

冒泡排序 bubble sort

简单冒泡排序实现过程

初始序列 【50 13 55 97 27 38 49 65】

第1趟排序结果 【13 50 55 27 38 49 65】97

第2趟排序结果 【13 50 27 38 49】55 65 97

第3趟排序结果 【13 27 38 49】50 55 65 97

第4趟排序结果 13 27 38 49 50 55 65 97

 

实现思想

分为有序区和无序区，对无序区从前向后一次比较相邻的值，从而使得较大的值向后移，较小的值向前移

就像水中的气泡，体积大的先浮上来，从前到后浮上来

 

平均时间性能

On^2

 

使用分治法思想 n*log2 n

归并排序

简单归并排序实现过程

初始序列 【8 3 6 7 1 5 4】

第1趟排序结果 【8 3 2 6】 【7 1 5 4】

第2趟排序结果 【8 3】【2 6】 【7 1】【5 4】

第log2 n趟排序 8 3 2 6 7 1 5 4 //拆成了长度为1的子序列，然后进行排序合并

第4趟排序结果 [3 8] [2 6] [1 7] [4 5]

第5趟排序结果 [2 3 6 8] [1 4 5 7]

最终趟排序结果 [1 2 3 4 5 6 7 8]

 

实现思想

划分： 将序列对半划分，直到划分为n个长度为1的子序列

求解子问题：分别对这两个子序列进行排序，得到两个有序的子序列

合并：将这两个有序的子序列合并成一个有序的序列，依次递归上去

合并实现原理：

在一开始的时候开辟一个一半长度的空间，用来复制储存第一部分序列来与第二部分序列进行比较和交换。

当右边的序列的值比左边的小得时候，将右移到左边，同时，复制的第三序列的该值移到右，（因为已经保证序列是升序了所以才可以这样做，这样时间复杂度仅为n）

平均时间性能

O(n*log2 n)

空间复杂度

O(n)

 

快速排序

简单快速排序实现过程

1.第一次划分，取到中位数，以中位数为轴，分成左右两个子序列，施行第二次划分

初始序列 【 i23】13 35 6 19 50【j28】

右侧扫描直到j<23 【i23】13 35 6【j19】50 28

r[i]与r[j]交换，i++ 19【i13】35 6【j23】50 28

左侧扫描直到r[i]>23 19 13【i35】6【j23】50 28

r[i]与r[j]交换,j-- 19 13【i23】【j6】35 50 28

右侧扫描直到j<23 19 13【i23】【j6】35 50 28

r[i]与r[j]交换，i++ 19 13 6【i j 23】35 50 28

当i==j，取得中值23 19 13 6 [23] 35 50 28

 

2.第二及之后的划分

第一次划分之后 【19 13 6】 23【35 50 28】

分别进行快速排序 【6 13】19 23【28】35【50】

6 【13】19 23 28【35】50

最终结果 6 13 19 23 28 35 50

 

 

实现思想

划分：第一次排序选定一个值作为轴值，以轴值为基准将整个序列划分为两个子序列

求解子问题：分别对划分后的每一个子序递归处理，直到子序列长度为1

合并：对子序列就地排序，因为已经排好了，直接合并不需要执行任何操作

平均时间性能

O(n*log2 n)

最坏时间复杂度，很少情况，基本可以避免

O（n^2）

空间复杂度

O(n)

 

使用减治法思想

插入排序

简单插入排序实现过程

初始序列 12 [15 9 20 10 6]

第1趟排序结果 12 15 [9 20 10 6]

第2趟排序结果 9 12 15 [20 10 6]

第3趟排序结果 9 12 15 20 [10 6]

第4趟排序结果 9 10 12 15 20 [6]

第5趟排序结果 6 9 10 12 15 20

 

实现思想

属于减治法的减--技术，每一趟排序后将问题规模减1，基本思想是：

一次将带排序序列中的每一个记录插入到一个已经排好序的序列中，直到全部记录都排好序。

插入方法：将这个值与前面的值进行挨个比较，直到最终找到合适的位置之后，将值复制，其他的值往后挪一位，这个值插入。也就是比我大的往右边挪

平均时间性能

O（n^2）

空间复杂度

O(n)

实现代码

其中的v称为哨兵

 

 

 

 

希尔排序 shell Sort(递减增量排序)

简单希尔排序实现过程

初始序列 8 7 6 5 4 3 2 1

第1趟排序4列 4 3 2 1 8 7 6 5

第2趟排序2列 2 1 4 3 6 5 8 7

第3趟排序1列 1 2 3 4 5 6 7 8

 

队列：4列

前

8 7 6 5

4 3 2 1

后

4 3 2 1

8 7 6 5

队列：2列

前

4 3

2 1

8 7

6 5

后

2 1

4 3

6 5

8 7

 

实现思想

把序列看成是一个矩阵，分成m列，逐列进行排序，具体有多少列，希尔这个人给出的标准是n/2^k，也就是16分成4列，1248这样子分,32分成5列，124816这样子分。以16为例子，先分成8列，每列2个进行排序，再分成4列，每个4列进行排序，在分成8列，每列2个进行排序，最后分成一个规则的1列，这一列是非常规则的（有点像归并排序）。规则到21,43,65,87,109这样，最后对这个1列进行排序，每趟之后逆序对的数量在逐渐减少就是希尔算法。其底层是一个插入排序，插入排序逆序对越少，效率越高，算是对插入排序的改进，即分列＋插入。

平均时间性能

O（nlog2 n）

最坏时间复杂度

O（n^2），改进后为O（n^3/4）

空间复杂度

O(1)

 

 

堆排序

 

 

平均时间性能

O（nlog2 n）+n 舍去n为简单大根堆排序实现过程

1.对序列进行原地建大根堆

初始序列 28 35 20 32 18 12

第1趟28与35交换 35 28 20 32 18 12

第2趟28与32交换 35 32 28 18 20 12

 

2.对建立好的大根堆进行堆升序排序

初始大根堆序列 35 32 28 18 20 12

去根节点与末尾交换 12 32 28 18 20 [35]

重塑堆 32 20 28 12 18 [35]

重复去根节点 18 20 28 12 [32 35]

重塑堆 28 20 18 12 [32 35]

去根节点 12 20 18 [28 32 35]

重塑堆 20 12 18 [28 32 35]

去根节点 18 12 [20 28 32 35]

最终 12 18 20 18 32 35

 

3.对建立好的大根堆进行堆升序排序

初始大根堆序列 35 32 28 18 20 12

去根节点重塑堆 [35] 32 28 18 20 12

去根节点重塑堆 [35 32] 28 18 20 12

去根节点重塑堆 [35 32 28] 20 18 12

去根节点重塑堆 [35 32 28 20 ] 18 12

去根节点重塑堆 [35 32 28 20 18 ] 12

最终 [35 32 28 20 18 12]

 

实现思想

堆是具有每个节点的值都大于或者等于（大根堆）其左右孩子节点的值得性质的完全二叉树

大根堆：47 35 26 20 18 7 13 10

小根堆：7 10 13 18 35 26 47 20

每个节点的子节点为2n与2n+1，如第一个节点的子节点为1*2与3

减治法思想：通过每次把根节点减去来解决整个排序问题

 

实现想法

将比节点值大的子节点的值进行互换，然后跟选择排序一样，将元素位置进行替换，算是更快速的选择排序：O（nlog2 n）

其中建立堆得时间复杂度为n

其中重塑堆的时间复杂度为log2 n

 

建堆和堆去顶重塑代码实现

 

 

 

重构堆

 

 

 

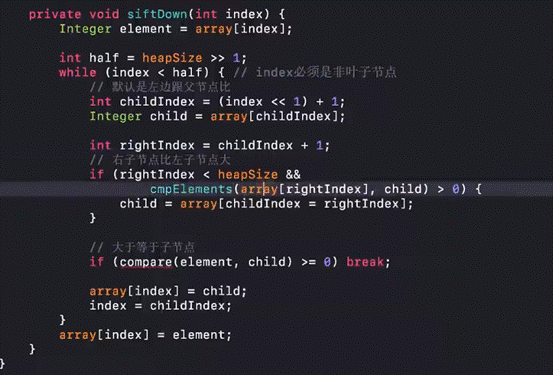
其他不是基于比较的排序算法，利用空间换时间

计数排序

实现思想1

适合对一定范围内的整数进行排序

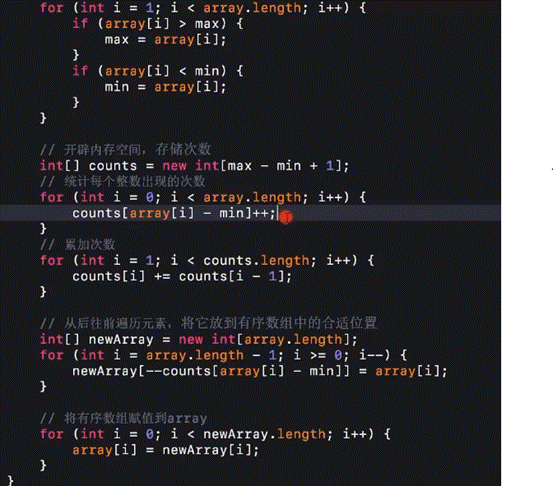
先遍历一次，找到最大值i，创建一个长度为序列中最大值i的序列（默认值都是0），然后统计每个整数在序列之后出现的次数（将整数变成新数组的索引，而其索引对应的内容则为词频，输出除去索引0之外的其他内容非0的索引就行了），然后按着次数输出到一个新的序列里面就可以了，就这样子就实现了排序。核心是统计每个整数出现的次数（有点像当初的凡科的面试题，也有点像hash表＋链表，也就是hashset或者hashmap）

 

 

 

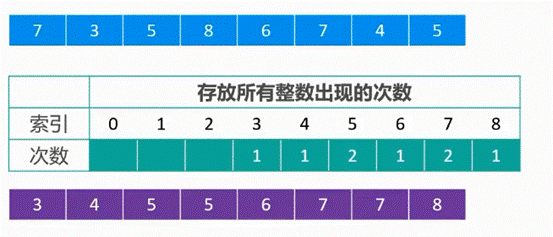
实现思想改进

根据最大值创建的数列长度：最大值减去最小值，数组下标加上最小值就是元素值。满足负数要求，如果最小数是100，则省了100个空间

将出现的次数变成也就是新序列的值变成原序列的长度，保证了更快的效率。并且可以保证稳定性！，因为我又创建了第二个新数组，第二个新数组通过第一个新数组的关系将原数组的内容赋值到第二新数组中，所以保持了稳定性。

遍历：从后往前遍历元素

 

 

 

 

 

 

简单技术排序实现过程

 

 

 

 

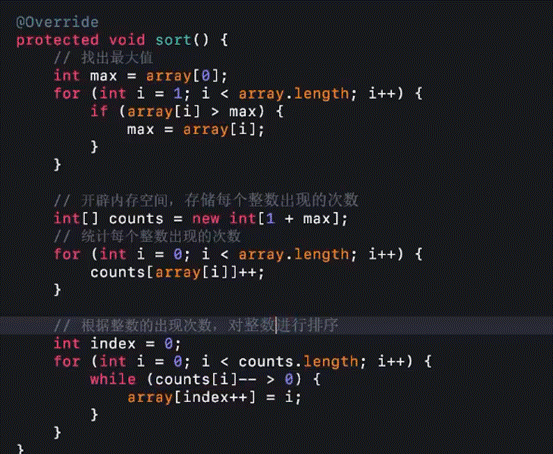
精髓是这个：

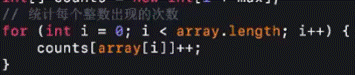
改进实现代码

 

 

 

 

 

平均时间性能

O（n+k）

空间复杂度

O（n+k）

 

 

基数排序

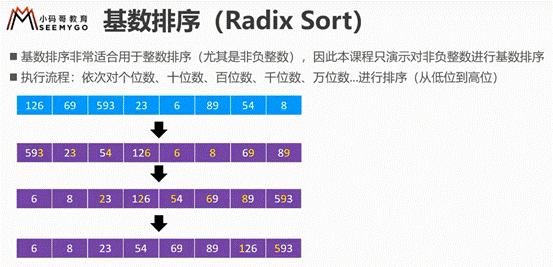
简单基数排序实现过程

 

 

 

另一种，但是空间复杂度会非常高，会很费空间

 

 

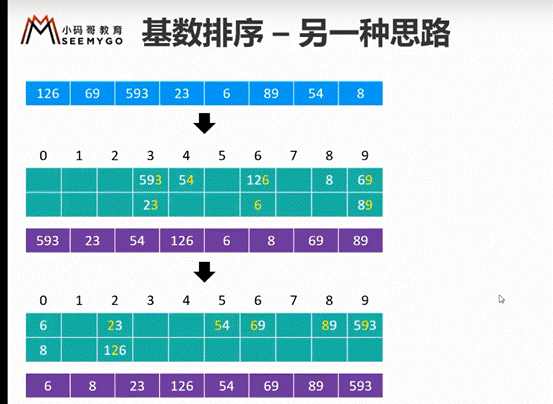
实现思想

针对非负整数进行排序

依次对个十百千位数进行排序，反过来不行，因为你不知道这个数到底有几位

底层因为只要排0-9，所以可以用计数排序，而计数的索引的值仍然是次数。

 

 

 

 

桶排序

简单桶排序实现过程

跟hash表也有点相似

 

 

 

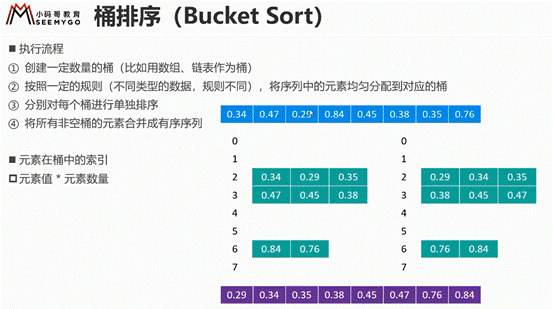
实现思想

 

 

平均时间性能

O（nlog2 n-nlogm）

其中分桶大概是n，对每个桶进行排序，假设用快速排序，将是nlog2 n级别，所以这个的时间复杂度有点难说，看你每个桶用什么排序

空间复杂度

O(n+m)

 

 

附件：

 

 

排序的稳定性

所以=号一般不要随便乱用，用了之后可能就不稳定了，也有可能变稳定了（选择排序）用=会尽量变稳定。

严格来说选择排序不是稳定的排序

冒泡排序不加=是稳定排序

 

 

原地算法

 

 

传说中的最强排序

new个数为数组的长度的线程，new了n和线程，每个线程睡眠的时间就是其值，这样值小的最会先醒过来抢时间片，并打印出结果，传说中的空间复杂度O1，时间复杂度On

 

 谢谢。