L1 和L2正则化在机器学习里面的应用,拉普拉斯分布和高斯分布
正则化是为了防止过拟合。
1. 范数
范数是衡量某个向量空间(或矩阵)中的每个向量以长度或大小。
范数的一般化定义:对实数p>=1, 范数定义如下:
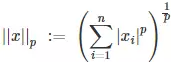
L1范数:
当p=1时,是L1范数,其表示某个向量中所有元素绝对值的和。
L2范数:
当p=2时,是L2范数, 表示某个向量中所有元素平方和再开根, 也就是欧几里得距离公式。
在二维情况下,不同范数的图形如下, q表示的是范数p的值:
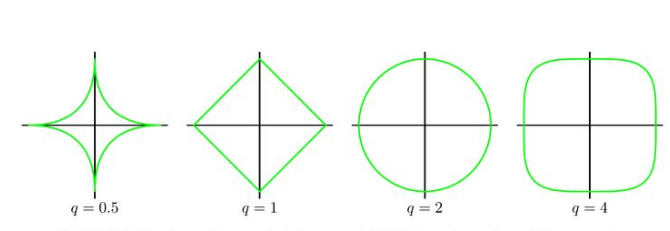
那么在机器学习中他们是什么区别呢?
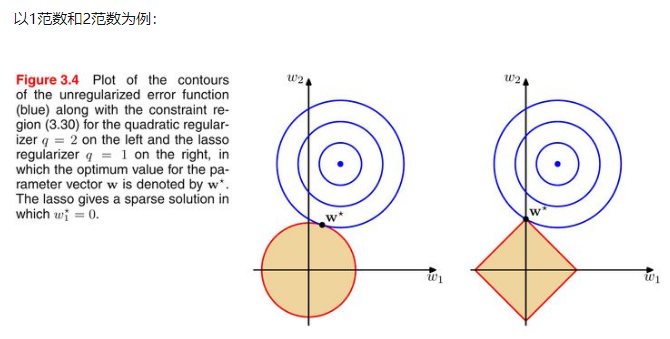
蓝色圈圈表示loss function求解的值,红色圈表示范数的正则,圆是2范数,方形是1范数。可以看到,
由于1范数是菱形(顶点是凸出来的),其相切的点更可能在坐标轴上,而坐标轴上的点有一个特点,其只有一个坐标分量不为零,其他坐标分量为零,即是稀疏的。
由于2范数解范围是圆,所以相切的点有很大可能不在坐标轴上, 比较容易是稠密值。
结论:1范数在机器学习中可以稀疏解。 2范数在机器学习中可以导致稠密解。
另外,2范数可以解决矩阵求逆病态问题,并且求解过程比梯度下降SGD要快。
2范数解决矩阵求逆病态问题: 矩阵求逆是一个病态问题,即矩阵并不是在所有情况下都有逆矩阵。所以在实际使用时会遇到问题。
为了解决这个问题,可以求其近似解。可以用SGD(梯度下降法)求一个近似解,或者加入正则项(2范数)。
加入正则项是我们这里要说的。加入2范数的正则项可以解决这个病态问题,并且也可以得到闭式解,在实际使用时要比用SGD快。
2范数的正则项还有其他好处: 比如控制方差和偏差的关系,得到一个好的拟合。
2. 拉普拉斯分布
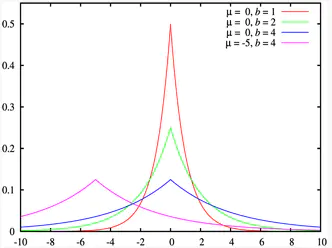
如果随机变量的概率密度函数分布为:
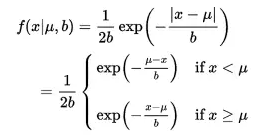
那么它就是拉普拉斯分布。其中,μ 是数学期望,b > 0 是振幅。如果 μ = 0,那么,正半部分恰好是尺度为 1/2 的指数分布。
3.高斯分布
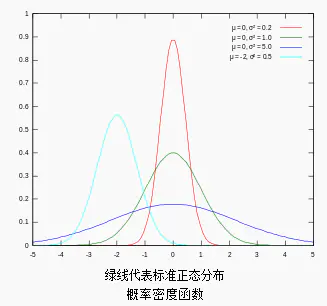
又叫正态分布,若随机变量X服从一个数学期望为μ、标准方差为σ2的高斯分布,记为:
X∼N(μ,σ2),
则其概率密度函数为:
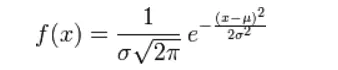





 浙公网安备 33010602011771号
浙公网安备 33010602011771号