神经网络[翻译|总结|第二课]
原文:cs229-notes2
生成学习算法(Generative Learning algorithms)
不同于判别式学习算法,生成学习算法是对特征的分布的建模。
步骤:对p(y)和p(x|y)进行建模之后,用贝叶斯公式来推导y的分布
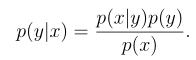
1.高斯判别分析(GDA)
1.1 多元正态分布(多变量高斯分布)
分布N(µ,Σ)中,μ是平均值向量,Σ是协方差矩阵。密度函数为:
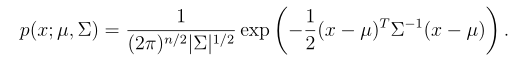
随着协方差矩阵Σ变大,高斯分布的形态就变得更宽平(spread-out),而如果协方差矩阵Σ变小,分布就会更加集中(compressed)
1.2 高斯判别分析模型
假如分类问题的输入特征X是一系列的连续值随机变量,我们可以使用GDA模型。
y ∼ Bernoulli(Φ)
x|y = 0 ∼ N(µ 0 ,Σ)
x|y = 1 ∼ N(µ 1 ,Σ)
概率密度函数分布式如下
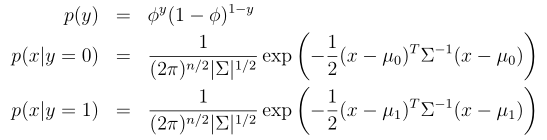
其中的参数是Φ、Σ、μ0、μ1(注意,虽然这里有两个不同方向的均值向量μ0 和 μ1,针对这个模型还是一般只是用一个协方差矩阵)
取对数的似然函数:
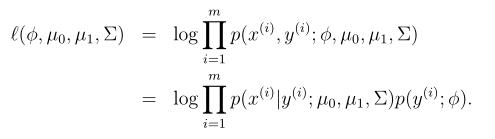
通过使 l 取得最大值,找到对应的参数组合,然后就能找到该参数组合对应的最大似然估计:

1.3 讨论:GDA和逻辑回归
把变量 p(y = 1|x;Φ,µ 0 ,µ 1 ,Σ)作为一个x的函数,它可以被表示为如下的形式:
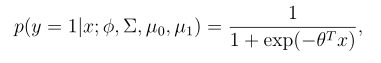
其中θ是Φ,Σ, μ0, μ1的某种函数,这就是逻辑回归对p (y = 1|x)建模的形式。
总结:高斯判别分析方法(GDA)能够建立更强的模型假设,并且在数据利用上更加有效(比如说,需要更少的训练集就能有“还不错的”效果),当然前提是模型假设争取或者至少接近正确。逻辑回归建立的假设更弱,因此对于偏离的模型假设来说更加健壮(robust)得多。然而,如果训练集数据的确是非高斯分布的(non-Gaussian),而且是有限的大规模数据(in the limit of large datasets),那么逻辑回归几乎总是比GDA要更好的。因此,在实际中,逻辑回归的使用频率要比GDA高得多
2.朴素贝叶斯方法
在GDA中,特征向量x是连续的,值为实数的向量,这一节是x是离散值时使用的一种算法。
1.选特征向量
2.建立生成模型
建模p(x|y)时做一个强假设:假设向量xi对于给定的y时独立的(朴素贝叶斯假设)
实际上,即使一些原始的输入值是连续的,也可以转换成一个小规模的朴素贝叶斯方法。例如,如果用特征向量xi表示住房面积,可以按下表方法来对输入变量进行离散化。

2.1 拉普拉斯光滑
在先前有限的训练数据集中没见过的一件事,就认为这种事件的概率为0,这不是一个好的方式。要避免因此产生的分子分母同时为0,要引入拉普拉斯光滑,对分子加1,对分母加k,此时的朴素贝叶斯对参数估计变成如下形式:
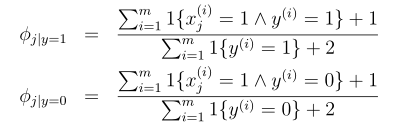



 浙公网安备 33010602011771号
浙公网安备 33010602011771号