[CTS2024] 多方计算

首先 \(\sum_{i=0}^{n-1}a_i\) 的位数 \(bit=m+\lceil\log_2n\rceil\)。我们以 \(n=m=5\) 为例。此时 \(bit=8\)。

我们把 \(\sum_{i=0}^ja_i\) 第 \(k\) 位的值累加为 \(b_{j,k}\)。考虑 \(b_{j,k-1},b_{j-1,k}\) 都确定之后可以确定 \(b_{j,k}\)，然后把它传输到下一个位置。如果 \(i<n\)，则该位清零。

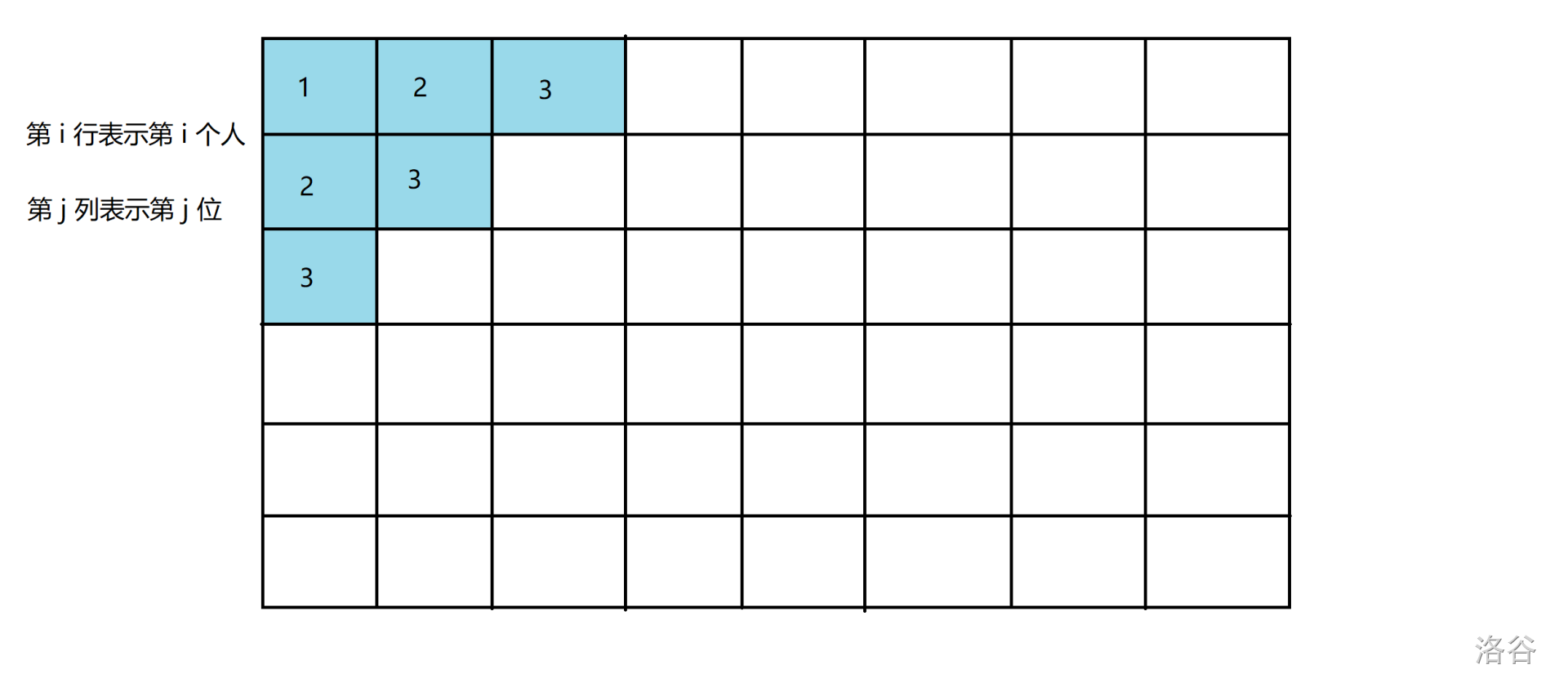
如图，浅蓝色区域确定了 \(b_{j,k}\)，其中数字表示第几轮被确定。设第 \(r\) 轮被确定，则 \(j+k+1=r,k=r-j-1\)。

这个做法的次数为 \(n+bit\)。

考虑让 \(r-j-1<0\) 的 \(j\) 也传输信息，传递第 \(bit+(r-j-1)\) 位。那么此时相当于两路并行传输，如图：

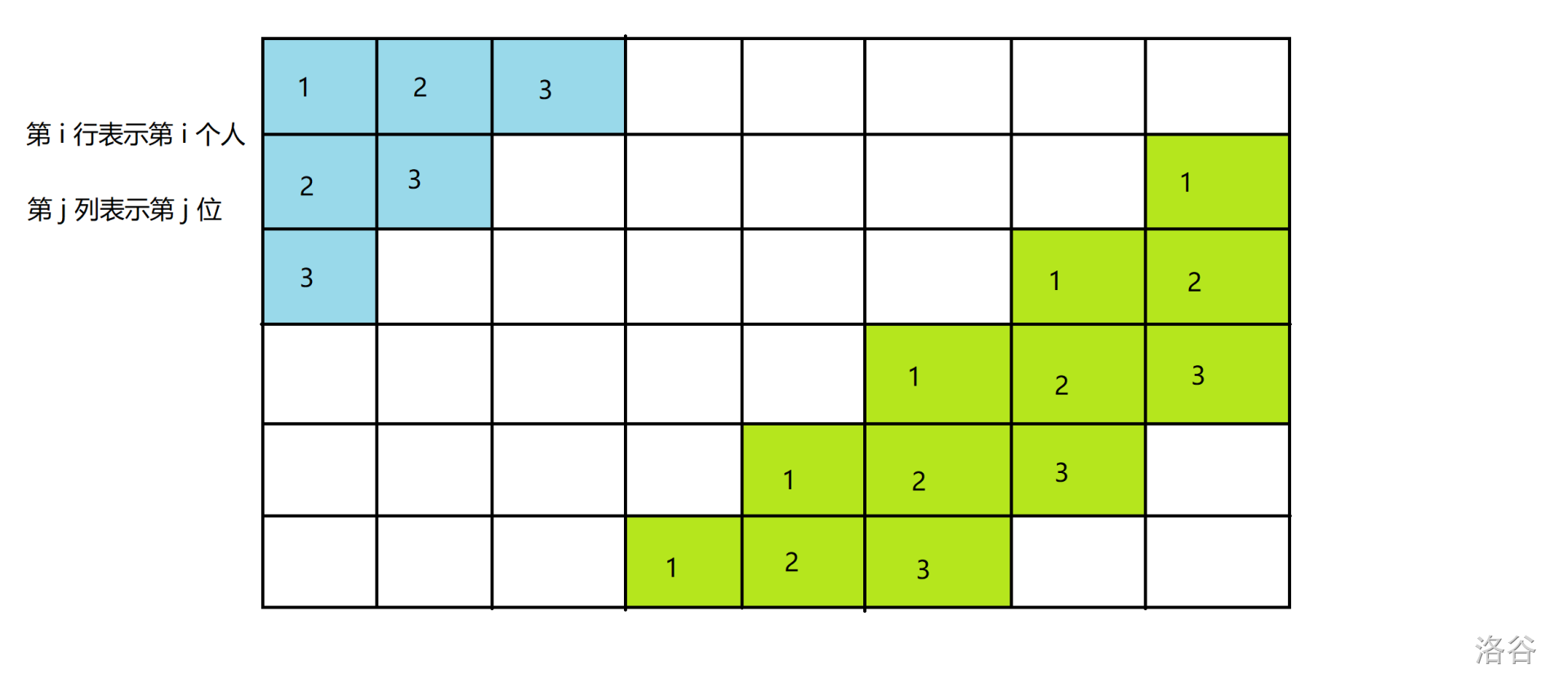
浅蓝色部分和浅绿色部分并行扩展。现在考虑这个做法的次数是多少。

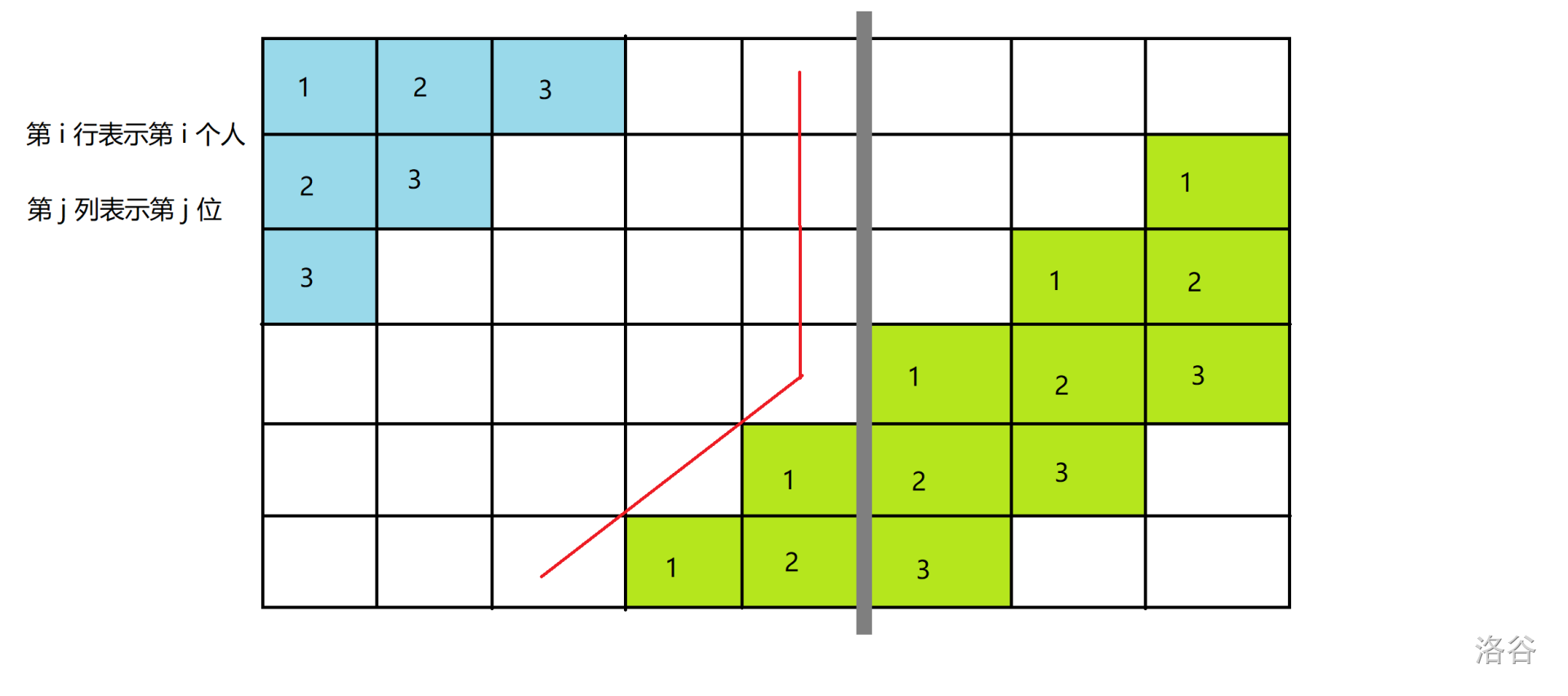
灰线分隔了低 \(m\) 位和高 \(\lceil\log_2n\rceil\) 位，注意浅绿色部分经过 \(n\) 轮扩展完毕后格子全部清零。对于浅蓝色部分扩展的总贡献总是在红线以内。

前 \(\lceil\log_2n\rceil+1\) 个人最多贡献 \(2^m-1\)，后面的人根据 \(2^k-1>2(2^{k-1}-1)\) 最多贡献 \(2^m-1\)，这样是 \((\lceil\log_2n\rceil+2)(2^m-1)\)，最多 \(m+\lceil\log_2(\lceil\log_2n\rceil+2)\rceil\) 位，总共要传输 \(n+m+4\) 轮。

考虑三路并行，大概这样：

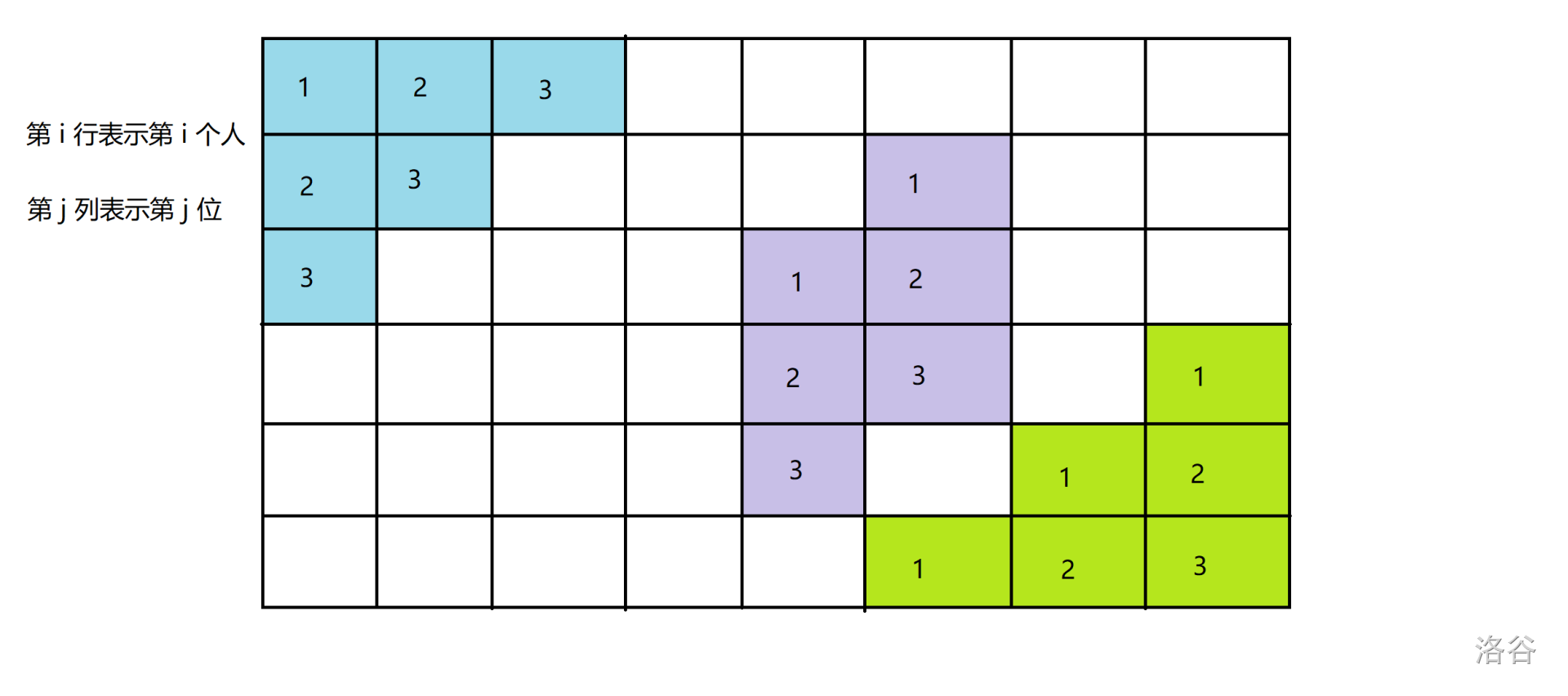
最终清零的位置为紫色和浅绿色扩展区域的并（第 \(n\) 行除外）。次数变为 \(n+m+3\)，可以通过。

https://uoj.ac/submission/793259