命题、
1. "x+5>0",这是一个命题。
2.设A,B,C,D为任意集合,则命题“若A⊆C且B⊆D,则有A×B⊆C×D”是真命题
<=> (((p∨q)→r)→s)∧(s→((p∨q)→r))
<=> (¬((p∨q)→r)∨s)∧(¬s∨((p∨q)→r))
<=> (¬(¬(p∨q)∨r)∨s)∧(¬s∨(¬(p∨q)∨r))
<=> (¬((¬p∧¬q)∨r)∨s)∧(¬s∨((¬p∧¬q)∨r))
<=> (¬((¬p∨r)∧(¬q∨r))∨s)∧(¬s∨((¬p∨r)∧(¬q∨r)))
<=> ((¬(¬p∨r)∨¬(¬q∨r))∨s)∧(¬s∨((¬p∨r)∧(¬q∨r)))
<=> (((p∧¬r)∨(q∧¬r))∨s)∧(r∨¬s∨(¬p∧¬q)∨(¬p∧r)∨(¬q∧r))
<=> (p∧¬r∧¬s)∨(q∧¬r∧¬s)∨(r∧s)∨(¬p∧¬q∧s)∨(¬p∧r∧s)∨(¬q∧r∧s) (析取范式) 极小
<=> (p∨q∨s)∧(p∨¬r∨s)∧(q∨¬r∨s)∧(¬r∨s)∧(¬p∨¬q∨r∨¬s)∧(¬p∨r∨¬s)∧(¬q∨r∨¬s) (合取范式)极大
一个命题是永真式当且仅当它的析取范式包含一个命题符号及其否定式
一个命题是永假式当且仅当它的合取范式包含一个命题符号及其否定式
在题目的情况下,原命题为可满足式
若令r=¬p,那么析取范式化为:
(p∧¬s)∨(p∧q∧¬s)∨(¬p∧s)∨(¬p∧¬q∧s)
再令s=¬p,化为:p∨(p∧q)∨¬p∨(¬p∧¬q)
此时,析取范式包含p和¬p,即为永真式。
<==> ┐(p∨(q ∧r))∨(p∧q∧r)
<==> (┐p∧(┐q∨┐r))∨(p∧q∧r)
<==> (┐p∧┐q)∨(┐p∧┐r)∨(p∧q∧r)
<==> (┐p∧┐q∧r)∨(┐p∧┐q∧┐r)∨(┐p∧q∧┐r)∨(┐p∧┐q∧┐r)∨(p∧q∧r)
<==> (┐p∧┐q∧┐r)∨(┐p∧┐q∧r)∨(┐p∧q∧┐r)∨(p∧q∧r)
<==> m0∨m1∨m2∨m7 (主析取范式)
<==> M3∧M4∧M5∧M6 (主合取范式)
由此可得成真赋值为000, 001, 010, 111,成假赋值为011, 100, 101, 110。
方法一是用真值表求主析取范式,找到成真赋值01,10,11,转化为十进制是1,2,3,所以主析取范式是m1∨m2∨m3。主合取范式是M0。
方法二就是一般做法,进行等值演算
( p→q)→( q∨p)
<=> ┐(┐p∨q)∨(p∨q)
<=> (p∧┐q)∨(p∨q) 前者即为m2
<=> (p∧┐q)∨(p∧1)∨(1∧q)
<=> (p∧┐q)∨(p∧(┐q∨q))∨((┐p∨p)∧q)
<=> (p∧┐q)∨(p∧┐q)∨(p∧q)∨ (┐p∧q)∨(p∧q)
<=> (p∧┐q)∨(p∧q)∨ (┐p∧q)
<=> m2∨m3∨m1
<=> m1∨m2∨m3
命题公式 ┐(p→q)∧q∧r的成真赋值是( )
000,001,010,011,100,101,111
无成真赋值,公式为矛盾式
公式为重言式,所有赋值均为真
000,010,011
令F(x):x是鸟;G(x):x会飞翔。则“鸟都会飞翔”这个命题可符号化为( )
∃x(F(x)→G(x))
∃x(F(x)∧G(x))
∀x(F(x)→G(x))
∀x(F(x)∧G(x))
!∀x(F(x)→G(x))
∀x(F(x)→┐G(x))
∀x(F(x)∧┐G(x))
∃x(F(x)→G(x))
∃x(F(x)∧G(x))
∀x(F(x)∧G(x))
∀x(F(x)→G(x))
令F(x):x是人;G(x):x爱看电影。则“没有不爱看电影的人”这个命题可符号化为( )
∃x(F(x)→G(x))
∀x(F(x)∧┐G(x))
∃x(F(x)∧G(x))
┐∃x(F(x)∧┐G(x))
命题:∃xF(x),其中F(x):5x=1,此命题在下列个体域中为假命题()
(1)自然数集合N(N中含0)
(2)整数集合Z
(3)实数集合R
(1)和(2)
(1)和(3)
(2)和(3)
(1),(2)和(3)都是
谓词公式∀x∃y(x•y=0)在下列哪个个体域中真值为1( )
(1)实数集合 R
(2)整数集合 Z
(3)正整数集合 Z+
(4)R-{0}(非零实数集合)
(1)和(2)
(1)和(3)
(2)和(3)
(3)和(4)
谓词公式∃x∀y(x•y=0)在下列哪个个体域中真值为1( )
(1)实数集合 R
(2)整数集合 Z
(3)正整数集合 Z+
(4)R-{0}(非零实数集合)
(1)和(3)
(2)和(3)
(1)和(2)
(1),(2)和(4)
谓词公式∀x∃y(x•y=1)在下列哪个个体域中真值为1( )
(1)实数集合 R
(2)整数集合 Z
(3)正整数集合 Z+
(4)R-{0}(非零实数集合)
(1),(2)和(3)
(1)和(4)
(4)
(3)
谓词公式∃x∀y(x•y=1)在下列哪个个体域中真值为1( )
(1)实数集合 R
(2)整数集合 Z
(3)正整数集合 Z+
(4)R-{0}(非零实数集合)
(1)
(2)
(3)
(1),(2),(3),(4)都不是
谓词公式∀x∃y(x•y=x)在下列哪个个体域中真值为1( )
(1)实数集合 R
(2)整数集合 Z
(3)正整数集合 Z+
(4)R-{0}(非零实数集合)
(1)和(2)
(3)和(4)
全部都不是
全部都是
谓词公式∃x∀y(x•y=x)在下列哪个个体域中真值为1( )
(1)实数集合 R
(2)整数集合 Z
(3)正整数集合 Z+
(4)R-{0}(非零实数集合)
(1)和(2)
(3)和(4)
(1)和(3)
(2)和(4)
设解释为:个体域 D={-2,3,6},a=3,一元谓词F(x):x≤3,G(x):x>5,R(x):x≤7,在此解释下,下面各式的真值为1的有( )
(1)∀x(F(x)∧G(x))
(2)∀x(R(x)→F(x))∨G(a)
(3)∃x(F(x)∨G(x))
(1)
(2)
(3)
(1)和(2)
从集合分类的角度看,命题公式可分为( )
永真式、矛盾式
永真式、可满足式、矛盾式
可满足式、矛盾式
永真式、可满足式
集合A={1,2,3},令R={<1,1>,<2,2>,<3,3>,<1,2>},则R具有( )
自反性
反自反性
对称性
传递性
设集合A={a,b,c},令关系 R={<b,c>,<c,b>},则R具有( )
自反性
反对称性
反自反性
传递性
集合A={1,2,3,4,5,6,7,8},等价关系R={<x,y>∧x≡y(mod 3)},A在R下的商集A/R=( )
{{1,4,7},{2,5,8},{3,6}}
{1,4,7,2,5,8,3,6}
{1,2,3}
{{1},{2},{3}}
设集合A={a,b,c,d,e},偏序关系R的哈斯图下图所示,则元素的关系不正确的是( )
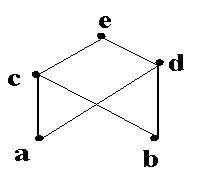
c ≤ d
a ≤ e
a < c
d ≤ e
已知A,B是集合│A│=15,│B│=10,│A∪B│=20,则│A∩B│=( )
10
5
20
13
集合X={a,b,c,d,e},Y={1,2,3,4},f从X到Y的映射,其中f(a)=2,
f(b)=4,f(c)=1,f(d)=3,f(e)=4,则f是( )
双射
满射
单射
不是单射也不是满射
下列命题中,( )是真命题。
若2+2=4,则3+3=6
若2+2=4,则3+3≠6
若2+2≠4,则3+3=6
若2+2≠4,则3+3≠6
取个体域为整数集,给定下列各式,真命题的为( )
∀x∃y(x•y=0)
∀x∃y(x•y=1)
∃y∃x(x•y=2)
x-y=-y+x
设 S = {Φ,{1},{1,2}},则有( )∈ S。
{1,2}
1
1,2
Φ,{1}
S1=Φ,S2 = {Φ},S3=P( {Φ}),S4=P( Φ),下列是真命题的有( )
S2∈S4
S1⊆S3
S4⊆S2
S4∈S3
笛卡尔积运算具有如下性质()
A×Φ=Φ×B=Φ
当A≠B且A,B都不是空集时,A×B≠B×A
当A,B,C都不是空集时,(A×B)×C≠A×(B×C)
A×(B∩C)=(A×B)∩(A×C)
集合A={1,2,3,4,5,6,7,8},等价关系R={<x,y>∧x≡y(mod 3)},关于等价类[x]
,如下结论正确的是( )
[1]=[4]=[7]={1,4,7}
[2]=[5]=[8]={2,5,8}
[3]=[6]={3,6}
[1]=[2]=[3]={1,2,3}
集合A={a,b,c,d},下列子集族是A的划分的是( )
{{a},{b,c},{d}}
{{a,b},{c},{a,d}}
{{a,b,c,d}}
{Φ,{a,b},{c,d}}
有100个程序员,其中47名熟悉C语言,35名熟悉Java语言,23名熟悉两种语言,那么,有
在1和1000之间不能被5或6,也不能被8整除的数的个数是
某班有25个学生,其中14人会打篮球,12人会打排球,6人会打篮球和排球,5人会打篮球和网球,还有2人会打这3种球,而6个会打网球的人都会打另外一种球(指篮球或排球),则不会打这3种球的人数是
一个班里有50个学生,在第一次考试中有26人得5分,在第二次考试中有21人得5分,如果两次考试中都没得5分的有17人,那么两次考试都得5分的有
设集合 A={{1},1},则幂集P(A)的基数|P(A)|=
集合 A={a,b},集合B={0,1,2},则A和B的笛卡尔积的基数|A×B|是
集合 A={a,b},则幂集P(A)和A的笛卡尔积的基数|P(A)×A|是
设S={1,2},则S上可以定义


 浙公网安备 33010602011771号
浙公网安备 33010602011771号