概率论02
作者:桂。
时间:2018-06-27 06:22:47
链接:https://www.cnblogs.com/xingshansi/p/9232042.html
接上文:概率论01
以下推理的基础是:切比雪夫不等式,且都要符合独立同分布。 而切比雪夫不等式的前提是:不同变量具有独立的分布即可。
第五章
1- 大数定律(Law of Large Numbers,LLN)
1)随机变量X1,X2,....相互独立
2)服从同一分布
3)数学期望E(Xk) = mu,k = 1,2,...
则有:
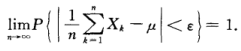
证明:
借助切比雪夫不等式:
P{|x-mu| >= epsilon} <= sigma^2/epsilon^2
假设方差存在,求解方差sigma^2:
【同一分布 + 独立性,才有该性质】
得出:
n->∞,夹逼准则:
大数定律:1)独立同分布;2)具有均值mu,在1)2)条件满足的情况下,随机变量样本数n很大时,他们的算术平均值非常接近期望【依概率收敛】。 大数定律理论上证明了该常识。
2- 伯努利大数定律(Bernoulli’s Law of Large Numbers)
对于n重伯努利试验,事件A的频率依概率收敛于其概率。 伯努利大数定律为
该问题针对的是n重伯努利试验
证明:
可知mu = np,又fA是事件A发生的次数
fA = X1 + X2 +...
则fA/n =
,期望为p,借助大数定律:
3- 中心极限定理(The Central Limit Theorem (CLT))
中心极限定理:客观实际通常是大量的相互独立的随机因素的综合影响,其中每一个别因素在总的影响中所起的作用都是微小的,这种随机变量往往近似服从正态分布,这种现象就是中心极限定理的客观背景。
3.1- 中心极限定理
1)独立同分布;2)均值、方差存在,则对于:
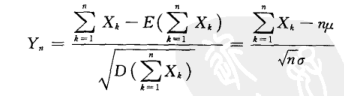
其分布函数为正态分布:
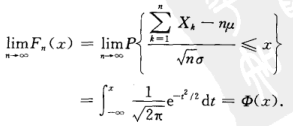
证明:
借助特征函数【见最后附录】
利用特征函数的三个基本性质【3个特性易证,细节略】
1)若n阶矩存在,
2)X = X1 +X2+X3+... Xi满足独立同分布,则特征函数 phei(X) = phei(∑Xi) = phei(X1)phei(X2)phei(X3)...
3)分布函数可由特征函数唯一确定【即傅里叶变换,时域、频域存在一一对应关系,特征函数为傅里叶变换的共轭】
定义:
以上性质由特征函数1)2)特性求得。
两边取对数,令
,根据洛必达法则【洛必达法则证明可由:拉格朗日中值定理或柯西中值定理证明】
又exp(-t^2/2)对应标准正态分布,根据特征函数3),得证。
特征函数与矩、分布函数,都可以建立联系,这方面的运算都可以借助特征函数。
理论细节可参考附件1。
3.2- 李雅普诺夫(Lyapunov)定理
基本没用到过,略。
该定理不要求具有同分布特性,即方差满足给定约束,大数(n很大)仍然服从正态分布。
3.3- 棣莫弗-拉普拉斯定理(De Moivre-Laplace)
该定理是3.1中心极限定理的特例,此处mu = np, D = sigma^2 = np(1-p),带入即可。该定理证明了大数情况下,二项分布与正态分布的关系。
附录:
特征函数定义:
最开始是母函数,主要为了方便N阶矩的计算而引入:
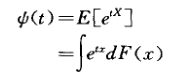
对于t = 0,有
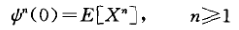
但母函数可能不存在,如引入特征函数,易证特征函数一定存在。特征函数:
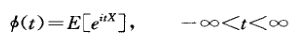 ,可以看出这是傅里叶变换的共轭。
,可以看出这是傅里叶变换的共轭。
对于性质2,可结合二维傅里叶变换来理解:
F(u,v) = 积分1 积分2 f(x,y)exp(-i[xu + yv]) dxdy对于独立的情况 = F(u)*F(v),多维变量依次类推。
另外,对于正态分布,特征函数为:
性质: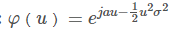
原始表达式为:

可借助常微分方程求解,细节略。
有了MATHMATICA这个工具,像这样的微分,可以借助工具完成:
支持指令输入:
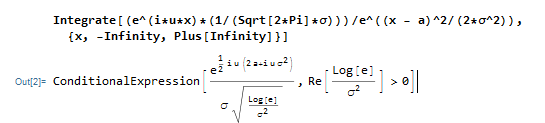
也可直接编辑公式:
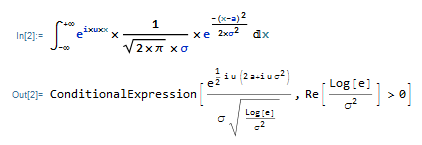
可见特征函数存在的前提是方差>0。


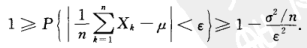
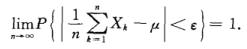
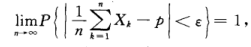
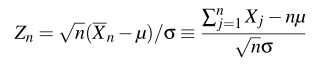
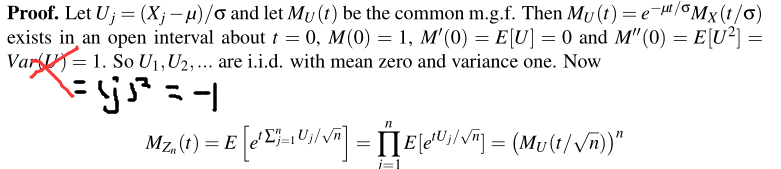


 浙公网安备 33010602011771号
浙公网安备 33010602011771号