机器学习入门——线性回归算法

什么是线性回归？

线性回归是一种用于预测连续值的监督学习算法。它假设输入（特征）和输出（目标）之间存在线性关系，模型公式为：

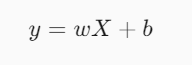
其中：

y：预测值。
X：输入特征。
w：权重（斜率）。
b：偏置（截距）。

损失函数：均方误差（MSE）​

为了衡量模型的预测效果，我们使用 ​均方误差（MSE）​ 作为损失函数：

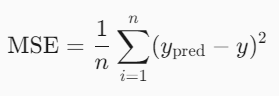
优化方法：梯度下降法

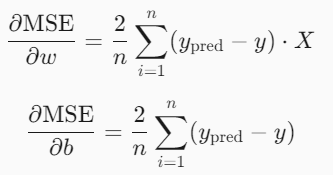
代码实现

import numpy as np
import matplotlib.pyplot as plt

# 生成数据
np.random.seed(42)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

# 初始化参数
w = np.random.randn(1)
b = np.random.randn(1)

# 定义超参数
learning_rate = 0.1
n_epochs = 100

# 训练模型
for epoch in range(n_epochs):
    # 预测值
    y_pred = w * X + b
    
    # 计算损失（MSE）
    loss = np.mean((y_pred - y) ​** 2)
    
    # 计算梯度
    dw = (2 / len(X)) * np.sum((y_pred - y) * X)
    db = (2 / len(X)) * np.sum(y_pred - y)
    
    # 更新参数
    w -= learning_rate * dw
    b -= learning_rate * db
    
    # 打印损失
    if epoch % 10 == 0:
        print(f"Epoch {epoch}, Loss: {loss}")

# 可视化结果
plt.scatter(X, y, color='blue', label='Data')
plt.plot(X, w * X + b, color='red', label='Linear Regression')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.show()

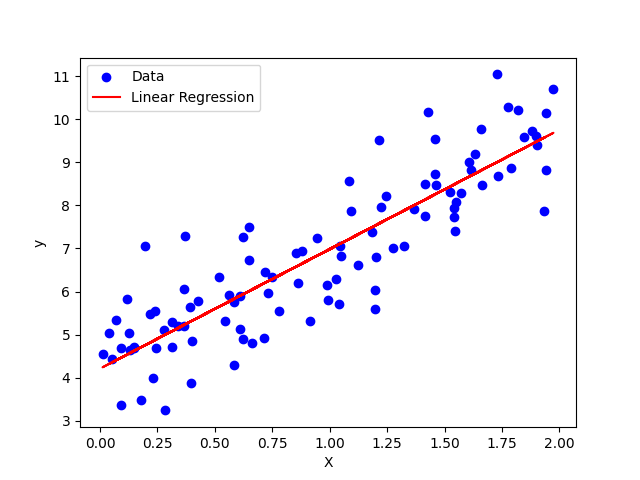
一些问题

1 为什么需要初始化参数？

• 初始化参数是模型训练的起点。
• 随机初始化可以避免模型陷入局部最优。

2 学习率的作用是什么？

• 学习率控制参数更新的步长。
• 如果学习率太大，模型可能无法收敛；如果学习率太小，模型收敛速度会很慢。

3 梯度是如何计算的？

• 梯度是损失函数对参数的偏导数。
• 通过梯度，我们可以知道参数应该往哪个方向调整才能使损失函数减小。

4 为什么损失函数是均方误差？

• 均方误差可以很好地衡量预测值与真实值之间的差距。
• 它是凸函数，便于优化。