★P1364 医院设置——图最短路径问题（Floyd算法）

题目描述

设有一棵二叉树，如图：

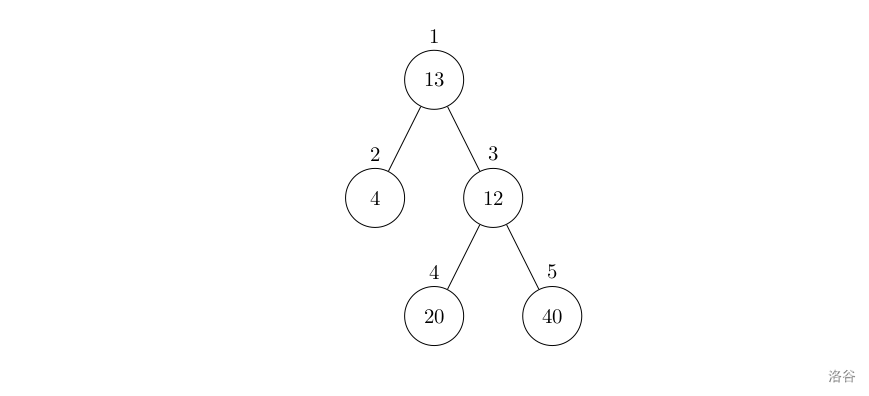
其中，圈中的数字表示结点中居民的人口。圈边上数字表示结点编号，现在要求在某个结点上建立一个医院，使所有居民所走的路程之和为最小，同时约定，相邻接点之间的距离为 \(1\)。如上图中，若医院建在 \(1\) 处，则距离和 \(=4+12+2\times20+2\times40=136\)；若医院建在 \(3\) 处，则距离和 \(=4\times2+13+20+40=81\)。

输入格式

第一行一个整数 \(n\)，表示树的结点数。

接下来的 \(n\) 行每行描述了一个结点的状况，包含三个整数 \(w, u, v\)，其中 \(w\) 为居民人口数，\(u\) 为左链接（为 \(0\) 表示无链接），\(v\) 为右链接（为 \(0\) 表示无链接）。

输出格式

一个整数，表示最小距离和。

输入输出样例 #1

输入 #1

5						
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0

输出 #1

81

说明/提示

数据规模与约定

对于 \(100\%\) 的数据，保证 \(1 \leq n \leq 100\)，\(0 \leq u, v \leq n\)，\(1 \leq w \leq 10^5\)。

P1364 医院设置

题目描述

设有一棵二叉树，如图：

其中，圈中的数字表示结点中居民的人口。圈边上数字表示结点编号，现在要求在某个结点上建立一个医院，使所有居民所走的路程之和为最小，同时约定，相邻接点之间的距离为 \(1\)。如上图中，若医院建在 \(1\) 处，则距离和 \(=4+12+2\times20+2\times40=136\)；若医院建在 \(3\) 处，则距离和 \(=4\times2+13+20+40=81\)。

输入格式

第一行一个整数 \(n\)，表示树的结点数。

接下来的 \(n\) 行每行描述了一个结点的状况，包含三个整数 \(w, u, v\)，其中 \(w\) 为居民人口数，\(u\) 为左链接（为 \(0\) 表示无链接），\(v\) 为右链接（为 \(0\) 表示无链接）。

输出格式

一个整数，表示最小距离和。

输入输出样例 #1

输入 #1

5						
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0

输出 #1

81

说明/提示

数据规模与约定

对于 \(100\%\) 的数据，保证 \(1 \leq n \leq 100\)，\(0 \leq u, v \leq n\)，\(1 \leq w \leq 10^5\)。

题解

#include <bits/stdc++.h>
using namespace std;
int main() {
    int n;
    cin>>n;
    vector<int> population(n+1);
    vector<int> left(n+1); vector<int> right(n+1);
    // 1.初始化邻接矩阵0，对角线INF
    int dist[110][110];
    for (int i=1;i<=n;i++) {
        for (int j=1;j<=n;j++) {
            if (i==j) dist[i][j]=0;
            else dist[i][j]=INT_MAX;
        }
    }
    // 2.构建边，默认权值（边长）1
    // （输入边的端点）
    for (int i=1;i<=n;i++) {
        cin>>population[i]>>left[i]>>right[i];
    }
    
    for (int i=1;i<=n;i++) {
        if (left[i]!=0) {
            dist[i][left[i]]=1;
            dist[left[i]][i]=1;
        }
        if (right[i]!=0) {
            dist[i][right[i]]=1;
            dist[right[i]][i]=1;
        }
    }
    // 3.Floyd三重循环分别求两点之间最短路径长
    for (int k=1;k<=n;k++) {
        for (int i=1;i<=n;i++) {
            for (int j=1;j<=n;j++) {
                if (dist[i][k]!=INT_MAX&&dist[k][j]!=INT_MAX) {
                    dist[i][j]=min(dist[i][j],dist[i][k]+dist[k][j]);
                }
            }
        }
    }
    // 4.根据题意，求最小和
    int min_sum=INT_MAX;
    for (int i=1;i<=n;i++) {
        int sum=0;
        for (int j=1;j<=n;j++) {
            sum+=dist[i][j]*population[j];
        }
        min_sum=min(min_sum,sum);
    }
    cout<<min_sum;
}