ZKY题解
P6772 [NOI2020] 美食家
ZKY解题思路
蒟蒻语
wtcl,只会最简单的题目
这道题目与 P6569 [NOI Online #3 提高组]魔法值(民间数据)类似,都是倍增优化矩阵乘法。
蒟蒻解
首先观察数据, 看到 \(w_{i} \leq 5\) , 可以想到储存下前 5 天的状态, 从而推出现在的状态。
显然着这样是 \(O(nwT)\) 的,不可通过次题。
但是考虑到 \(n\) 很小,可以使用矩阵乘法优化。然后按照图建立矩阵 \(a\) 。大概是这样子的:
原来的数组 (now表示转移结束后的状态):
| now-5 | now-4 | now-3 | now-2 | now-1 |
要变成:
| now-4 | now-3 | now-2 | now-1 | now |
转移矩阵 \(a\) :
| 0 | 0 | 0 | 0 | w=5的转移 |
| S | 0 | 0 | 0 | w=4的转移 |
| 0 | S | 0 | 0 | w=3的转移 |
| 0 | 0 | S | 0 | w=2的转移 |
| 0 | 0 | 0 | S | w=1的转移 |
\(S\) 表示单位矩阵
形如这样子的:
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
矩阵快速幂即可。时间复杂度为 \(O((nw)^3\log T)\)
但是这只是没有美食节的情况, \(k = 0\) 。对于每次美食节, 可以先把答案算到美食节的时间 -1 。然后对原来建立的矩阵进行矩阵快速幂, 时间复杂度 \(O(k(nw)^3 \log T)\) , 不可通过本题。
考虑继续优化。矩阵快速幂多次计算了一个矩阵的 \(2^{t}\) 次方,考虑优化调这个时间。倍增预处理出原矩阵的 \(2^{t}\) 次方。这部分的代码:
void build() {
btd[0] = a; // btd 是倍增矩阵。
for (int i = 1; i <= 30; i++) btd[i] = btd[i - 1] * btd[i - 1];
// 利用2^t-1矩阵的信息处理出2^t的矩阵。
}
求值时拿原来的序列乘以需要乘的矩阵。那么这部分的代码是:
void get(ll *f, int b) {
for (int i = 0; i <= 30; i++) if (b & (1 << i)) cf(f, btd[i]);
// cf: 乘法,代表数组(1*(nw)的矩阵)乘以矩阵
}
预处理时间复杂度是 \((nw^3)\log T\) ,而单次求值是 \((nw^2)\log T\) ,求 \(m\) 次就是 \(m(nw)^2\log T\) ,总时间复杂度是 \((nw^3)\log T + m(nw)^2\log T,\) 可以通过本题。
代码实现
点击查看代码
int mn;
struct M {
ll a[255][255];
} a;
M clear() {
M res;
for(int i = 1; i <= mn; i++) for(int j = 1; j <= mn; j++) res.a[i][j] = -inf;
return res;
}
M operator * (M aa, M bb) {
M res = clear();
for(int i = 1; i <= mn; i++)
for(int j = 1; j <= mn; j++)
for(int k = 1; k <= mn; k++)
res.a[i][j] = max(res.a[i][j], aa.a[i][k] + bb.a[k][j]);
return res;
}
M btd[33];
void cf(ll *f, M b) {
ll fz[255];
for(int i = 1; i <= mn; i++) fz[i] = f[i], f[i] = -inf;
for(int i = 1; i <= mn; i++)
for(int j = 1; j <= mn; j++)
f[i] = max(f[i], fz[j] + b.a[j][i]);
}
void get(ll *f, int b) {
for(int i = 0; i <= 30; i++) if(b & (1 << i)) cf(f, btd[i]);
}
void build() {
btd[0] = a;
for(int i = 1; i <= 30; i++) btd[i] = btd[i - 1] * btd[i - 1];
}
struct node {
int t, x, y;
} msj[2333];
bool cmp(node aa, node bb) {
return aa.t < bb.t;
}
int T, n, m, k, c[55];
ll ans[255];
int main() {
scanf("%d%d%d%d", &n, &m, &T, &k), mn = n * 5;
for(int i = 1; i <= n; i++) scanf("%d", &c[i]);
a = clear();
for(int i = 1; i <= 4 * n; i++) a.a[i + n][i] = 0;
for(int i = 1; i <= m; i++) {
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
a.a[u + n * (5 - w)][v + n * 4] = c[v];
}
build();
for(int i = 1; i <= k; i++)
scanf("%d%d%d", &msj[i].t, &msj[i].x, &msj[i].y);
sort(msj + 1, msj + k + 1, cmp);
for(int i = 1; i <= mn; i++) ans[i] = -inf;
ans[n * 4 + 1] = c[1];
for(int i = 1; i <= k; i++) {
get(ans, msj[i].t - msj[i - 1].t - 1);
M master = a;
for(int j = 1; j <= mn; j++) master.a[j][4 * n + msj[i].x] += msj[i].y;
cf(ans, master);
}
get(ans, T - msj[k].t);
if(ans[n * 4 + 1] < 0ll) puts("-1");
else printf("%lld\n", ans[n * 4 + 1]);
return 0;
}
CF830D Singer House
ZKY解题思路
首先考虑 dp 维护题目要求的深度为 i, 每个节点最多经过一次的不同有向路径数量 fi。
这样子这条路径是由原来的被蓝色圈圈包住的两个部分转移而来。
那么考虑记录 gi 为两条不相交的有向路径数量。
然后蒟蒻兴冲冲地去 尝试了, 并过了前两个样例,但是过不了第三个样例,这是为什么?
发现 gi 也有可能是由三条不相交的有向路径转移而来!
那么正解就浮出水面了:维护深度为 i, j 条不相交的有向路径数量 dpi,j。
转移如果想明白了状态其实很简单。这里还是说一下。
首先用背包求出深度为 i−1, 和为 j 条不相交的有向路径数量 : bb[j] += dp[i - 1][k] * dp[i - 1][j - k]
第一种转移:根结点独立,然后其他的路径让两个子树自由组合 : dp[i][j] += bb[j - 1] + 2 * dp[i - 1][j - 1]
第二种转移:路径不包括根结点,或根结点为路径起点或终点: dp[i][j] += (2 * j + 1) * bb[j] + (4 * j + 2) * dp[i - 1][j]
第三种转移:路径包括根结点,且连接两条原来在子树中是两条链: dp[i][j] += j * (j + 1) * bb[j + 1] + 2 * j * (j + 1) * dp[i - 1][j + 1]
代码实现
点击查看代码
#include<bits/stdc++.h>
#define L(i, j, k) for(int i = j; i <= k; i++)
#define R(i, j, k) for(int i = j; i >= k; i--)
using namespace std;
const int N = 444;
const int mod = 1e9 + 7;
int n, dp[N][N], bb[N];
int main() {
scanf("%d", &n);
dp[1][1] = 1;
L(i, 2, n) {
fill(bb, bb + n + 1, 0);
L(j, 1, n) L(k, 0, j) (bb[j] += 1ll * dp[i - 1][k] * dp[i - 1][j - k] % mod) %= mod;
dp[i][1] = 1;
L(j, 1, n) {
int t = 0;
(dp[i][j] += (2ll * j + 1) * bb[j] % mod) %= mod;
(dp[i][j] += (4ll * j + 2) % mod * dp[i - 1][j] % mod) %= mod;
(dp[i][j] += 1ll * j * (j + 1) % mod * bb[j + 1] % mod) %= mod;
(dp[i][j] += 2ll * j * (j + 1) % mod * dp[i - 1][j + 1] % mod) %= mod;
(dp[i][j] += bb[j - 1] % mod) %= mod;
(dp[i][j] += 2ll * dp[i - 1][j - 1] % mod) %= mod;
}
}
printf("%d\n", dp[n][1]);
return 0;
}
P6025 线段树
ZKY解题思路
这题十分在考场上十分坑,调了1个多小时后结果是题目出锅了,现在说一下我的做法。
10pts
暴力,在这里不展开了。
40pts
对于一珂线段树,我们只要走最大的那条路,并得到最终节点坐标即可。具体方法如下: 假设我们走到一个节点,它的子树共有x个节点,它的下标为y, 要求的是子树上最大下标:
- 首先如果
x==1,直接返回y - 否则,如果
x%2==0,返回的最大下标一定在右子树。 - 否则,如果
lowbit(x/2)==x/2表示左子树深度深,返回的最大下标一定在左子树。 - 否则,直接返回右子树(因为右子树相同深度下标一定比左子树大)
复杂度O(nlogn) n=(r-l+1)
在这里就不开longlong了反正也过不了
代码:
#include<bits/stdc++.h>
using namespace std;
int l,r,S,SS,ans;
int lowbit(int x) {
return x&-x;
}
int q(int x,int y) {
if(x==1) return y;
if(x%2==0) return q(x/2,y*2+1);
else if(lowbit(x/2)==x/2) return q(x/2+1,y*2);
else return q(x/2,y*2+1);
}
int main() {
scanf("%d%d",&l,&r);
S=l;
while(1) {
SS=S;
for(int i = 40; i >= 0; i--) {
int QwQ=(1ll<<i);
if(q(S,1)==q(S+QwQ,1)) S+=QwQ;
}
if(S>=r) {
if((r-SS+1)%2) ans^=q(S,1);
printf("%d",ans);
return 0;
}
if((S-SS+1)%2) ans^=q(S,1);
++S;
}
return 0;
}
100pts
然后我发现,有非常多的连续的f(i)相同,比如f(1536)~f(2047)均相同,于是就想到了倍增处理。
最终如果连续的个数为奇数那么将ans异或其中的f函数值。
代码长度短,时间复杂度很低但为O(玄学)
代码:
#include<bits/stdc++.h>
using namespace std;
long long l,r,S,SS,ans;
long long lowbit(long long x) {
return x&-x;
}
long long q(long long x,long long y) {
if(x==(1ll)) return y;
if(!(x&(1ll))) return q(x/(2ll),y*(2ll)+(1ll));
else if(lowbit(x/(2ll))==x/(2ll)) return q(x/(2ll)+(1ll),y*(2ll));
else return q(x/(2ll),y*(2ll)+(1ll));
}
int main() {
scanf("%lld%lld",&l,&r);
S=l;
while(1) {
SS=S;
for(long long i = (40ll); i >= (0ll); i--) {
long long QwQ=((1ll)<<i);
if(q(S,(1ll))==q(S+QwQ,(1ll))) S+=QwQ;
}
if(S>=r) {
if((r-SS+(1ll))%(2ll)) ans^=q(S,(1ll));
printf("%lld",ans);
return 0;
}
if((S-SS+(1ll))%(2ll)) ans^=q(S,(1ll));
++S;
}
return 0;
}
P2051 [AHOI2009] 中国象棋
ZKY解题思路
只有每行每列都只有 ≤2 个炮,才会不能互相攻击
于是对于第 i 行,我们可以记录在这一行和这一行之上的 有一个炮的列数 (记为 j) 和有两个炮的列数 (记为 k)。让 dpi,j,k 则表示这样放置的方案数
→ 表示转移
状态转移 1 : 增加 0 个炮
- dpi−1,j,k→dpi,j,k
保持原来的状态
状态转移2:增加1个炮
- dpi−1,j+1,k−1×(j+1)→dpi,j,k
有一列从一个炮增加到了两个炮
- dpi−1,j−1,k×(m−j−k+1)→dpi,j,k
有一列从零个炮增加到了一个炮
状态转移3:增加2个炮
- dpi−1,j−1,k×j×(m−j−k+1)→dpi,j,k
有一列从零个炮增加到了一个炮,有一列从一个跑增加到了两个炮(可以是上一次增加炮的那一列)
- dpi−1,j−2,k×(2m−i−k+2)→dpi,j,k
有两列从零个炮增加到了一个炮
- dpi−1,j+2,k−2×(2j+2)→dpi,j,k
有两列从一个炮增加到了两个炮
代码实现
点击查看代码
#include<bits/stdc++.h>
#define mod 9999973
using namespace std;
long long c(int a) {
return a*(a-1)/2;
}
int n,m;
long long dp[101][101][101];
int main() {
scanf("%d%d",&n,&m);
dp[0][0][0]=1;
for(int i = 1; i <= n; i++) {
for(int j = 0; j <= m; j++)
for(int k = 0; k <= m-j; k++)
dp[i][j][k]=dp[i-1][j][k];
for(int j = 0; j <= m; j++)
for(int k = 1; k <= m-j; k++)
dp[i][j][k]+=dp[i-1][j+1][k-1]*(j+1);
for(int j = 1; j <= m; j++)
for(int k = 0; k <= m-j; k++)
dp[i][j][k]+=dp[i-1][j-1][k]*(m-j-k+1);
for(int j = 2; j <= m; j++)
for(int k = 0; k <= m-j; k++)
dp[i][j][k]+=dp[i-1][j-2][k]*c(m-j-k+2);
for(int j = 0; j <= m; j++)
for(int k = 2; k <= m-j; k++)
dp[i][j][k]+=dp[i-1][j+2][k-2]*c(j+2);
for(int j = 0; j <= m; j++)
for(int k = 1; k <= m-j; k++)
dp[i][j][k]+=dp[i-1][j][k-1]*j*(m-k-j+1);
for(int j = 0; j <= m; j++)
for(int k = 0; k <= m-j; k++)
dp[i][j][k]%=mod;
}
int ans=0;
for(int j = 0; j <= m; j++)
for(int k = 0; k <= m-j; k++)
ans=(ans+dp[n][j][k])%mod;
printf("%lld",ans);
return 0;
}
P4285 [SHOI2008] 汉诺塔
ZKY解题思路
通过递推,得出从第i个柱子移动j个盘子会移动到哪个盘子上和要多少步
在这篇萌新的题解中,A盘为第一个柱子,B是第二个,C是第三个
具体方法:
初始化:
首先我们可以先简化条件
我们珂以只留下从A,B,C柱子上如果有一个盘子,会移动到哪个盘子。移动步数为1。
珂以定义数组dp[i][j]表示第i个柱子移动j个盘子要移动的步数,to[i][j]表示从第i个柱子移动j个盘子会移动到哪个盘子
递推:
设toa=to[j][i-1]表示j柱有i−1个盘子会移动到toa盘上
设tob=6-j-toa表示除toa,j这两个柱子外的柱子
① to[toa][i-1]==tob
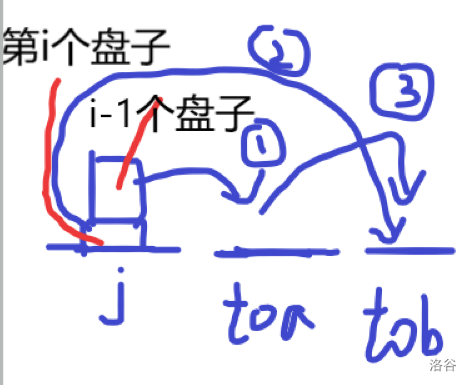
于是就有dp[j][i]=dp[j][i-1]+1+dp[toa][i-1],to[j][i]=tob;
②to[toa][i-1]==j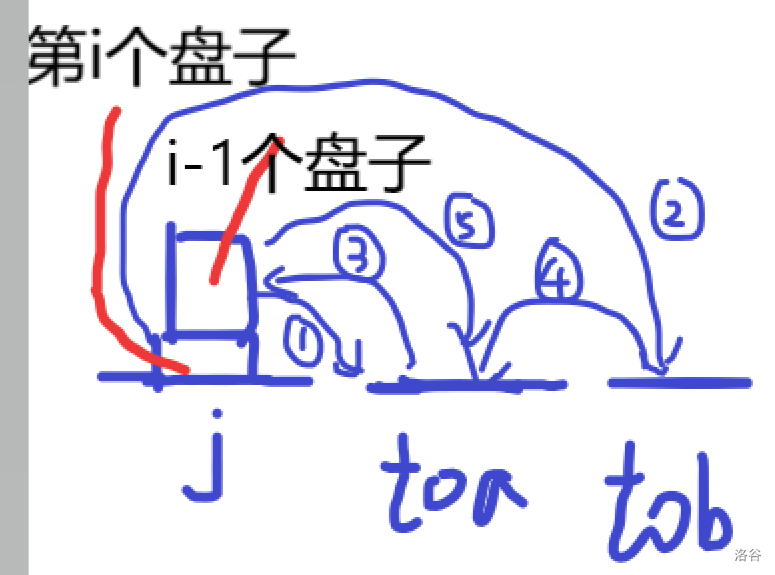
于是就有dp[j][i]=dp[j][i-1]+1+dp[toa][i-1]+1+dp[j][i-1],to[j][i]=toa;
代码实现
点击查看代码
#include<bit/stdc++.h>
long long dp[4][40],n,toa,tob,to[4][40],t[4][4];
char b[10];
int mian(){
scanf("%lld",&n);
for(int i = 1; i <= 6; i++) std::cin>>b,t[b[0]-'A'+1][b[1]-'A'+1]=7-i;
for(int i = 1; i <= 3; i++) toa=(i+1)%3+1,tob=i%3+1,to[i][1]=(t[i][toa]>t[i][tob]?toa:tob),dp[i][1]=1ll;
for(int i = 2; i <= n; i++) for(int j = 1; j <= 3; j++){
toa=to[j][i-1],tob=6-j-toa;
if(to[toa][i-1]==tob) dp[j][i]=dp[j][i-1]+1+dp[toa][i-1],to[j][i]=tob;
if(to[toa][i-1]==j) dp[j][i]=dp[j][i-1]+1+dp[toa][i-1]+1+dp[j][i-1],to[j][i]=toa;
}
printf("%lld",dp[1][n]);
}
CF724E Goods transportation
ZKY解题思路
题目就是说,有 \(n\) 个城市,1...n编号,每个城市生产 \(p_i\) 个货物,最多可卖掉 \(s_i\) 个货物。城市之间可以从编号小的往编号大的运输货物并卖出。求最大能卖出多少货物。
蒟蒻语
这是荀弱的第一道模拟费用流。
写个题解纪念以下吧。
蒟蒻解
首先是一个显然的网络流模型:
先建立一个超级源点与一个超级汇点。
然后把每一个点连向编号比它大的节点,流量为 \(c\) 。从超级源点向 \(i\) 连一条流量为 \(p_i\) 的边,从 \(i\) 向超级汇点连一条流量为 \(s_i\) 的边。最后求网络最大流。
这样显然不行,在见图方面就GG了。考虑到最大流 \(=\) 最小割,可以考虑到求解最小割。
显然可以把整张图分为两个集合,第一个集合包含超级源点 \(S\) ,向外输出流量;第二个集合包含超级汇点 \(T\) ,接受向该点流出的流量。
考虑到题目中说的从编号小的连向编号大的,说明了这是无后效性的。
所以可以考虑使用 \(dp_{i,j}\) 表示前 \(i\) 个节点中有 \(j\) 个节点是在第一个集合中的。
考虑 \(dp\) 转移方程:如果点 \(i\) 在第一个集合中,只要把该点到超级汇点 \(T\) 的边割掉即可;如果点 \(i\) 在第二个集合中,要把超级源点 \(S\) 到该店的边割掉,还要把之前向外输出流量的点(就是在第一个集合中的点)到该点的边割掉。
不难得到 \(dp\) 方程:
然而这样空间复杂度爆炸,只要把 \(dp\) 数组改称滚动数组即可
代码实现
点击查看代码
#include<bits/stdc++.h>
#define N 110000
using namespace std;
int n;
long long dp[2][N], c, s[N], t[N], Ans = 1e18;
int main() {
scanf("%d%lld",&n,&c);
for(int i = 1; i <= n; i++) scanf("%lld",&s[i]);
for(int i = 1; i <= n; i++) scanf("%lld",&t[i]);
for(int i = 1; i <= n; i++) dp[1][i] = 5e17;
for(int i = 1; i <= n; i++) {
dp[0][0] = dp[1][0] + s[i];
for(int j = 1; j <= i; j++) dp[0][j] = min(dp[1][j-1] + t[i], dp[1][j] + s[i] + c * j);
for(int j = 0; j <= i; j++) dp[1][j] = dp[0][j];
}
for(int i = 0; i <= n; i++) Ans = min(Ans, dp[1][i]);
printf("%lld\n", Ans);
return 0;
}
CF850F Rainbow Balls
ZKY解题思路
考虑最后变成哪一种颜色。
设 \(s = \sum_{i = 1}^{n}a_{i}\)
设现在有 \(k\) 种当前颜色,需要全部变成该种颜色,期望步数为 \(f_{k}\) 。
考虑状态转移。设 \(p\) 为取出两个球颜色不同的概率。
考虑 \(v_{i}\) 。由于我们考虑的 \(dp\) 是要求最后颜色是一定的,所以不能算上答案不是该颜色的答案。所以 \(v_{i}\) 就是最终颜色为这种颜色的概率。
如果颜色变动了,而让另一种颜色变成该颜色和该颜色变成另一种颜色的概率是一样的,所以 \(v_{i} = \frac{1}{2} (v_{i - 1} + v_{i + 1})\)
所以 \(2v_{i} = v_{i - 1} + v_{i + 1},v_{i + 1} - v_{i} = v_{i} - v_{i - 1}(= t)\)
又 \(v_{0} = 1, v_{s} = 1\)
所以 \(t = \frac{1}{s},v_{i} = \frac{i}{s}\)
所以 \(f_{i} = (f_{i + 1} + f_{i - 1})p + (1 - 2p)f_{i} + \frac{i}{s}\)
又 \(p = \frac{i(s - i)}{s(s - 1)}\)
当 \(i = 1\) 时,不需要考虑 \(f_{0} \circ 2f_{1} = f_{2} - 1\)
显然的, \(f_{s} = 0\)
而 \(f_{1} = f_{1} - f_{s} = \sum_{i - 2}^{s}f_{i} - f_{i - 1}\)
而 \(f_{1} - f_{2} = f_{1} - (2f_{1} - 1) = 1 - f_{1}\)
答案为 \(\sum_{i = 1}^{n}f_{a_i}\)
推到 \(\max(a_i)\) 即可。
代码实现
点击查看代码
#include<bits/stdc++.h>
#define N 2510
#define M 100010
#define mod 1000000007
using namespace std;
int qpow(int x, int y) {
if(x == 0) return 0;
int res = 1;
for(; y; x = 1ll * x * x % mod, y >>= 1) if(y & 1) res = 1ll * res * x % mod;
return res;
}
int n, s, qny, a[N], dp[M], cc, ans, maxn;
int main() {
scanf("%d", &n);
for(int i = 1; i <= n; i++) scanf("%d", &a[i]), s = (a[i] + s) % mod, maxn = max(maxn, a[i]);
dp[1] = 1ll * qpow(s, mod - 2) * (s - 1) % mod * (s - 1) % mod;
cc = (dp[1] - 1) % mod;
for(int i = 2; i <= maxn; i++) {
dp[i] = (cc + dp[i - 1]) % mod;
cc = (cc - 1ll * qpow((s - i + mod) % mod, mod - 2) * (s - 1) % mod + mod) % mod;
}
for(int i = 1; i <= n; i++) ans = (ans + dp[a[i]]) % mod;
printf("%d\n", ans);
return 0;
}
P6775 [NOI2020] 制作菜品
蒟蒻语
这题是真的不难, 蒟蒻同步赛上(反正是同步赛没关系)都想到背包了, 但是没看到 m≥n−2...
蒟蒻解
首先考虑 m≥n−1 的情况。
先说蒟蒻的贪心策略吧 :
每次取出最小的数, 如果他的值 <k, 再取出最小能和他加起来 ≥k 的数。
正确性如何呢?分两种情况考虑 : (以下 n>2)
- 没有比 k 小的数了。
那么就相当于从小到大排序后每次取出第一个数减 k,如果目前的值 x<k, 那么让第二个数 −(k−x), 由于第二个数 ≥k, 一定是可以减这么多的。所以一定可以取完。
2.有比 \(k\) 小的数。
取出数 \(x, x < k\) 。这时的最大数 \(\geq \frac{mk - x}{n - 1} = k * \frac{m}{n - 1} - \frac{x}{n - 1} \geq k - \frac{x}{n - 1}\)
而 \(k - \frac{x}{n - 1} + x = k + \frac{(n - 2)x}{n - 1} \geq k,\) 因此一定可以找到一个数加上他大于等于 \(k\) 。执行完该操作后 \(n - \dots, m - \dots,\) 所以仍然满足 \(m \geq n - 1\)
边界情况:
\(n = 1:m\) 次取完即可。
\(n = 2\) :若干次取完第一个数,若无剩余则 \(n = 1\) ,若有余数则取完第一个数然后取第二个数的一部分,然后就 \(n = 1\) 了。
该部分代码:
void work(int n, int m, int *d, int *tr) {
while(cnt < m) {
int minn = 0, mindy = 0;
for(int i = 1; i <= n; i++) if((d[i] < d[minn] || !minn) && d[i]) minn = i;
if(d[minn] >= k) {
++cnt;
ans[cnt][1] = tr[minn], ans[cnt][2] = k, d[minn] -= k;
continue;
}
for(int i = 1; i <= n; i++) if(i != minn && d[i] + d[minn] >= k && (d[i] < d[mindy] || !mindy)) mindy = i;
++cnt;
ans[cnt][1] = tr[minn], ans[cnt][2] = d[minn];
ans[cnt][3] = tr[mindy], ans[cnt][4] = k - d[minn];
d[mindy] -= k - d[minn], d[minn] = 0;
}
}
然后 \(m = n - 2\) 怎么弄/yiw
回想 \(m = n - 1\) 的情况。这种情况是 \(\sum_{i=1}^{n} a_i = (n - 1) * k\) 已经配好。这里是要求自己配出两个 \(\sum_{i=1}^{n} a_i = (n - 1) * k\) 。否则无解(这就说明如果将他划分之后再做,最大的那块还是 \(m \leq n - 2,\) 这时就考虑边界情况, \(n > 2, m = 1,\) 一定不行。再考虑因为不能划分了,所以每一次取是取两个数,而且取不完,一直保持 \(m \leq n - 2,\) 无解)。
那么怎么配呢?
考虑先把每一个数 \(-k\) ,就是要让几个数和为 \(-k\) 。
那么这样时间复杂度是 \(O(n^{2}m)\) , bitset 优化就是 \(O\left(\frac{n^{2}m}{w}\right)\) 了, 可以通过本题。
代码实现
点击查看代码
#include<bits/stdc++.h>
#define N 5100
#define FN 501
#define G 2000000
using namespace std;
int T, ans[N][5], k, cnt;
void work(int n, int m, int *d, int *tr) {
while(cnt < m) {
int minn = 0, mindy = 0;
for(int i = 1; i <= n; i++) if((d[i] < d[minn] || !minn) && d[i]) minn = i;
if(d[minn] >= k) {
++cnt;
ans[cnt][1] = tr[minn], ans[cnt][2] = k, d[minn] -= k;
continue;
}
for(int i = 1; i <= n; i++) if(i != minn && d[i] + d[minn] >= k && (d[i] < d[mindy] || !mindy)) mindy = i;
++cnt;
ans[cnt][1] = tr[minn], ans[cnt][2] = d[minn];
ans[cnt][3] = tr[mindy], ans[cnt][4] = k - d[minn];
d[mindy] -= k - d[minn], d[minn] = 0;
}
}
int n, m, d[N], pcnt, flag[FN], tr[N];
bitset<4000000> f[FN];
void dfs(int x, int wz) {
if(x == 0) return;
if(f[x - 1][wz] == 1) dfs(x - 1, wz);
else flag[x] = 1, dfs(x - 1, wz - d[x]);
}
int main() {
scanf("%d", &T);
while(T --> 0) {
scanf("%d%d%d", &n, &m, &k), cnt = 0;
for(int i = 1; i <= n; i++) scanf("%d", &d[i]), tr[i] = i;
if(m == n - 2) {
memset(f, 0, sizeof(f));
for(int i = 1; i <= n; i++) d[i] -= k;
f[0][G] = 1;
for(int i = 1; i <= n; i++) {
if(d[i] >= 0) f[i] = f[i - 1] | (f[i - 1] << d[i]);
else f[i] = f[i - 1] | (f[i - 1] >> -d[i]);
}
if(!f[n][G - k]) {
puts("-1");
continue;
}
else {
for(int i = 1; i <= n; i++) flag[i] = 0;
dfs(n, G - k), pcnt = 0;
for(int i = 1; i <= n; i++) d[i] += k;
for(int i = 1; i <= n; i++) if(flag[i] == 1)
++pcnt, swap(d[i], d[pcnt]), swap(tr[pcnt], tr[i]);
work(pcnt, pcnt - 1, d, tr);
work(n - pcnt, m, d + pcnt, tr + pcnt);
}
}
else work(n, m, d, tr);
for(int i = 1; i <= m; i++) {
printf("%d %d", ans[i][1], ans[i][2]);
if(ans[i][2] != k) printf(" %d %d", ans[i][3], ans[i][4]);
printf("\n");
}
}
return 0;
}
P6007 [USACO20JAN] Springboards G
解题思路
先将所有坐标的 \(y\) 坐标离散化。
然后把所有坐标按照 \(x\) 为第一关键字, \(y\) 为第二关键字排序。
从前往后遍历,用 \(dp_{i}\) 表示从 \((0,0)\) 到 \(x_{i}, y_{i}\) 的答案。
怎么更新信息?
考虑用 \(k\) 节点更新 \(i\) 节点。
如果 \(k\) 节点可以直接用跳板直接跳到 \(i\) 节点, 那么 \(dp\) 值相同。
否则要一步一步走过去。如果能更新, 那么 \(dp_{i} = dp_{k} + x_{i} - x_{k} + y_{i} - y_{k}\)
那么 \(dp_{i} - x_{i} - y_{i} = dp_{k} - x_{k} - y_{k}\)
如果设 \(f_{i} = dp_{i} - x_{i} - y_{i}\) ,那么 \(f_{i} = f_{k}!\)
那么现在丢掉 \(dp\) 数组然后使用 \(f\) 数组。
现在如果 \(k\) 节点可以直接用跳板直接跳到 \(i\) 节点
那么考虑谁能够更新他呢?
只有 \(x\) 坐标小于等于他而且 \(y\) 坐标小于等于他的节点可以更新。
这时显然 \(x\) 坐标小于等于 \(i\) 节点已经满足,而 \(y\) 坐标没有满足。现在要求 \(y\) 坐标处于 \(0 \dots y_{i}\) 的节点。
\(f_{i}\) 是 \(\min (f_{1,2\dots i - 1})\) ,显然每次把 \(f\) 值丢进树状数组里面就可以单次 \(O(\log n)\) 维护了
如果 \(i\) 是一个跳板的末端,直接更新一下就好了qwq
最后答案就是 \(\min (f_i + n + n)\) (如果把他当作一个节点,那么 \(f\) 值就是 \(\min (f_i)\) ,所以答案是 \(\min (f_i + n + n)\) )
代码实现
点击查看代码
#include<bits/stdc++.h>
#define N 200010
using namespace std;
int n, m, a[N], fr[N], to[N], Ans;
struct node {
int x, y, yy, id;
} p[N];
bool cmp(node aa, node bb) {
return aa.x == bb.x ? aa.y < bb.y : aa.x < bb.x;
}
bool ycmp(node aa, node bb) {
return aa.y < bb.y;
}
int ans[N];
void add(int x, int val) {
for(; x <= m * 2; x += (x & -x)) ans[x] = min(ans[x], val);
}
int qzh(int x) {
int Ans = 0;
for(; x; x -= (x & -x)) Ans = min(Ans, ans[x]);
return Ans;
}
int main() {
scanf("%d%d", &n, &m);
for(int i = 1; i <= m; i++) {
scanf("%d%d", &p[i].x, &p[i].y), p[i].id = i;
scanf("%d%d", &p[i + m].x, &p[i + m].y), p[i + m].id = i;
}
sort(p + 1, p + m * 2 + 1, ycmp);
p[0].y = -1;
for(int i = 1; i <= 2 * m; i++) p[i].yy = p[i - 1].yy + (p[i - 1].y != p[i].y);
sort(p + 1, p + m * 2 + 1, cmp);
for(int i = 1; i <= m * 2; i++) {
if(fr[p[i].id]) to[p[i].id] = i;
else fr[p[i].id] = i;
}
for(int i = 1; i <= m * 2; i++) {
a[i] = min(a[i], qzh(p[i].yy));
if(fr[p[i].id] == i) a[to[p[i].id]] = min(a[to[p[i].id]],
a[i] + p[i].x + p[i].y - p[to[p[i].id]].x - p[to[p[i].id]].y);
add(p[i].yy, a[i]);
Ans = min(Ans, a[i]);
}
printf("%d\n", Ans + n * 2);
return 0;
}
CF1137C Museums Tour
解题思路
本来不到 1 小时就写出来了, 数组却清空错了 QAQ
考虑到每一天博物馆开放情况是不相同的,可以把每一个博物馆一周的每一天的情况存下来,第 \(u\) 个博物馆 \(k\) 天的编号是 \(u + (k - 1)n\) 。每一条边 \((u, v)\) ,对于 \(\forall x \in [1, d]\) ,连一条 \((u + (x - 1)n, v + (x \mod d)n + v)\) 的边。
现在每一个点都对应着一个博物馆和一周中的某一天。
最后要求的是从1号点出发,能到达几个开着博物馆。
首先先缩点。
两个对应相同博物馆的要么缩完之后在统一个点,要么不联通
如何证明呢?sjy说很简单。
假设第 \(u\) 天对应的点能到第 \(v\) 天对应的点(不妨 \(v > u\) ),所以这个博物馆经过 \(v - u\) 天可以返回到自己。因此 \(lcm(n, v - u) - (v - u)\) 天后还是可以返回到这个博物馆。 \(lcm(u, v - u) - v - u \equiv (v - u) \pmod{n}\) 。
所以第 \(v\) 天对应的点可以到达 \(v - u\) 天前对应的点。所以第 \(v\) 天对应的点可以到达第 \(u\) 天到达的点。
所以现在只要先缩点, 然后统计一下缩了之后的点里面有多少种不同的博物馆开门的状态, 最后跑一遍最长路就好了。
代码实现
点击查看代码
#include<bits/stdc++.h>
#define N 100010
#define M 5000010
#define L(i, j, k) for(int i = j; i <= k; i++)
#define R(i, j, k) for(int i = j; i >= k; i--)
using namespace std;
bitset<M> vis, used;
bitset<N> day[55];
// bool [M];
int n, m, d, low[M], dfn[M], tot, bh[M], cnt, stot, st[M], dp[M], val[M];
int head[M], edge_id;
struct node {
int to, next;
} e[M];
void add_edge(int u, int v) { // 加边
++edge_id, e[edge_id].next = head[u], e[edge_id].to = v, head[u] = edge_id;
}
int gw(int x) { return (x - 1) % n + 1; } // 找这是哪一个点
int gd(int x) { return (x - 1) / n + 1; } // 找这是哪一天
inline void dfs(int x) { // tarjan 缩点, 已经手写栈了 QAQ
low[x] = dfn[x] = ++tot, st[++stot] = x, vis[x] = 1;
for(int i = head[x]; i; i = e[i].next) {
int v = e[i].to;
if(!dfn[v]) dfs(v), low[x] = min(low[x], low[v]);
else if(vis[v]) low[x] = min(low[x], dfn[v]);
}
if(low[x] == dfn[x]) {
int now = stot, pp;
++cnt;
while(st[now] != x) {
pp = st[now], bh[pp] = cnt, vis[pp] = 0, --now;
if(!used[gw(pp)] && day[gd(pp)][gw(pp)])
used[gw(pp)] = 1, val[cnt]++;
}
bh[x] = cnt, vis[x] = 0, --now;
if(!used[gw(x)] && day[gd(x)][gw(x)]) used[gw(x)] = 1, val[cnt]++;
L(i, now, stot) used[gw(st[i])] = 0;
stot = now;
}
}
int hd[M], eid;
struct ndeo {
int to, next;
} g[M];
void ad_edge(int u, int v) { // 加边
++eid, g[eid].next = hd[u], g[eid].to = v, hd[u] = eid;
}
inline int DFS(int x) { // DFS 找最长路
if(vis[x]) return dp[x];
for(int i = hd[x]; i; i = g[i].next) dp[x] = max(DFS(g[i].to), dp[x]);
vis[x] = 1, dp[x] += val[x];
return dp[x];
}
void rebuild() { // 缩点后建图
L(i, 1, n * d) for(int j = head[i]; j; j = e[j].next) {
int v = e[j].to;
if(bh[i] != bh[v]) ad_edge(bh[i], bh[v]);
}
}
char s[55];
int main() {
scanf("%d%d%d", &n, &m, &d);
L(i, 1, m) {
int u, v;
scanf("%d%d", &u, &v);
L(j, 1, d) add_edge(n * (j - 1) + u, n * (j % d) + v); // 连边
}
L(i, 1, n) {
scanf("%s", s + 1);
L(j, 1, d) day[j][i] = (s[j] == '1');
}
L(i, 1, n * d) if(!dfn[i]) dfs(i);
rebuild();
vis.reset();
printf("%d\n", DFS(bh[1]));
return 0;
}
CF1407D Discrete Centrifugal Jumps
蒟蒻语
到蒟蒻无人问津的博客园里看/kel
写了100行的线段树上ST表维护二分维护单调栈维护dp,结果最后发现只要俩单调栈就好了 \(= =\)
蒟蒻解
首先 \(dp_{i}\) 表示从1楼到 \(i\) 楼要跳几次。
题目中有3个条件,对三个条件分别设 \(dp\) 方程。
第一个很显然,就是 \(:dp_{i} = dp_{i - 1} + 1\)
第二个怎么弄呢?
考虑看有哪些点是可能来更新这个点的。
假设 \(x\) 位置可以来更新 \(i\) 位置。那么 \(h_x > \max(h_{x+1}, h_{x+2}, \ldots, h_{i-1})\) 。
考虑使用单调栈。单调栈里面的节点满足严格递增。这样 \(x\) 就一定是单调栈中的节点了
因为要求 \(h_i > \max(h_{x+1}, h_{x+2} \dots, h_{i-1})\) ,所以如果单调栈中有一个数比他大,那么单调栈中在他之后的节点就不能更新他了。
可以在单调栈中边弹点边更新答案。
第三个条件和第二个几乎一样,不说了。
蒟蒻码
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N = 3e5 + 7;
int n, m, s[N], dp[N], atot, a[N], btot, b[N];
int main() {
scanf("%d", &n);
for(int i = 1; i <= n; i++) scanf("%d", &s[i]);
memset(dp, 0x3f, sizeof(dp));
a[++atot] = 1, b[++btot] = 1, dp[1] = 0;
for(int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + 1;
while(atot && s[i] >= s[a[atot]]) {
if(s[i] != s[a[atot]]) dp[i] = min(dp[i], dp[a[atot - 1]] + 1);
--atot;
}
while(btot && s[i] <= s[b[btot]]) {
if(s[i] != s[b[btot]]) dp[i] = min(dp[i], dp[b[btot - 1]] + 1);
--btot;
}
a[++atot] = i, b[++btot] = i;
}
printf("%d\n", dp[n]);
return 0;
}
P6853 station
蒟蒻语
还是蒟蒻太菜了,这场 div1 竟然一题都没做出来/kk/kk/kk
蒟蒻解
首先我们把每 5 个点分为一组。然后分组结果大概是这样子:

可以看到首先下面需要有一条边来让整张图有一条支撑的路径。然后每一组内都有 6 条边。
那么这样子的图是可行的。原因:
- 对于每条线路,都至少经过两个车站,满足第一个条件。
- 对于所有点,经过他的路径数不超过 3,满足第二个条件。
- 对于任意两条边,都与最下面的那条边有交点,满足第三个条件。
那么可以先将边的数量-1,然后再按模6的余数分类,单独处理(细节看代码)。
小蒟蒻太菜了,不会证明这为什么这样点数是最小的。
蒟蒻码
点击查看代码
#include<bits/stdc++.h>
#define re register
#define L(i, j, k) for(re int i = j; i <= k; i++)
#define R(i, j, k) for(re int i = j; i >= k; i--)
#define db double
#define ll long long
using namespace std;
int n, m, tot;
void print(int x) { // 把每一个组内的点输出
L(i, 1, x) {
L(j, 1, 3) printf("2 %d %d\n", (i - 1) * 5 + 1, (i - 1) * 5 + 2 + j);
L(j, 1, 3) printf("2 %d %d\n", (i - 1) * 5 + 2, (i - 1) * 5 + 2 + j);
}
}
int main() {
scanf("%d", &n), n--; // 先在最下面放一条线
int ds = n / 6 * 5;
if(n % 6 == 0) {
printf("%d\n", ds);
printf("%d ", ds / 5 * 3);
L(i, 1, ds) if(i % 5 == 0 || i % 5 == 3 || i % 5 == 4) printf("%d ", i) // 输出这一个组内元素
puts("");
print(ds / 5);
}
else if(n % 6 == 1) {
ds -= 5; // 特别注意一下,为了让剩下的那条边有依靠,这里是把一个组再拆开来qwq
printf("%d\n", ds + 7);
printf("%d ", ds / 5 * 3 + 4);
L(i, 1, ds) if(i % 5 == 0 || i % 5 == 3 || i % 5 == 4) printf("%d ", i);
printf("%d %d %d %d\n", ds + 1, ds + 2, ds + 3, ds + 4);
print(ds / 5);
printf("2 %d %d\n", ds + 5, ds + 1); // 处理不属于那一组一组的那些边
printf("2 %d %d\n", ds + 5, ds + 2);
printf("2 %d %d\n", ds + 5, ds + 3);
printf("2 %d %d\n", ds + 6, ds + 2);
printf("2 %d %d\n", ds + 6, ds + 3);
printf("2 %d %d\n", ds + 7, ds + 1);
printf("2 %d %d\n", ds + 7, ds + 4);
} // 后面的分类讨论和上面的几乎一样
else if(n % 6 == 2) {
printf("%d\n", ds + 3);
printf("%d ", ds / 5 * 3 + 2);
L(i, 1, ds) if(i % 5 == 0 || i % 5 == 3 || i % 5 == 4) printf("%d ", i);
printf("%d %d\n", ds + 1, ds + 2);
print(ds / 5);
printf("2 %d %d\n", ds + 3, ds + 1);
printf("2 %d %d\n", ds + 3, ds + 2);
}
else if(n % 6 == 3) {
printf("%d\n", ds + 4);
printf("%d ", ds / 5 * 3 + 3);
L(i, 1, ds) if(i % 5 == 0 || i % 5 == 3 || i % 5 == 4) printf("%d ", i);
printf("%d %d %d\n", ds + 1, ds + 2, ds + 3);
print(ds / 5);
printf("2 %d %d\n", ds + 4, ds + 1);
printf("2 %d %d\n", ds + 4, ds + 2);
printf("2 %d %d\n", ds + 4, ds + 3);
}
else if(n % 6 == 4) {
printf("%d\n", ds + 4);
printf("%d ", ds / 5 * 3 + 2);
L(i, 1, ds) if(i % 5 == 0 || i % 5 == 3 || i % 5 == 4) printf("%d ", i);
printf("%d %d\n", ds + 1, ds + 2);
print(ds / 5);
printf("2 %d %d\n", ds + 3, ds + 1);
printf("2 %d %d\n", ds + 3, ds + 2);
printf("2 %d %d\n", ds + 4, ds + 1);
printf("2 %d %d\n", ds + 4, ds + 2);
}
else if(n % 6 == 5) {
printf("%d\n", ds + 5);
printf("%d ", ds / 5 * 3 + 3);
L(i, 1, ds) if(i % 5 == 0 || i % 5 == 3 || i % 5 == 4) printf("%d ", i);
printf("%d %d %d\n", ds + 1, ds + 2, ds + 3);
print(ds / 5);
printf("2 %d %d\n", ds + 4, ds + 1);
printf("2 %d %d\n", ds + 4, ds + 2);
printf("2 %d %d\n", ds + 5, ds + 1);
printf("2 %d %d\n", ds + 5, ds + 2);
printf("2 %d %d\n", ds + 5, ds + 3);
}
return 0;
}
CF1428F Fruit Sequences
蒟蒻语
蒟蒻7min切F,挽回了本一定掉分的局面/cy
| 342 | u repacui | 5114 | 499 00:01 | 981 00:06 | 968 00:10 | 1302 00:31 | 1364 01:09 | |
| 343 | zhoukangyang | 5109 | 494 00:04 | 883 00:21 | 911 00:28 | 1038 01:26 | 861 02:21 | 922 02:28 |
| 344 | cheetose | 5096 | 494 00:04 | 962 00:12 | 952 00:15 | 1268 00:38 | 1420 00:59 |
分竟然还没有别人5题高
(本题解为目前cf上的最短代码解!)
蒟蒻解
考虑计算对于每一个左端点的贡献。
所以可以考虑算这个左端点比后面的那个左端点多了多少贡献。
对于一个位置 \(l\)
- 这个位置是 0 : 没有多余贡献。
- 这个位置是 1 : 如果这个位置到这个联通块底部的长度为 \(k\) , 那么找到后面第一个出现连通块长度为 \(k\) 的位置 \(d\) , 那么右端点在 \([l, d - 1]\) 的答案都会加一, 比左端点为 \(l + 1\) 的贡献多了 \(d - l\) ; 如果找不到, 右端点在 \([d, n]\) 的答案都会加一, 那么比左端点为 \(l + 1\) 的贡献多了 \(n + 1 - l\) 。
给一张图以便理解:

然后考虑怎么维护这东西。
由于我们要找的是第一个出现联通块长的位置,那么我们可以在计算完长度为 \(k\) ,初始位置为 \(t\) 的连通块的贡献后,从左到右更新联通块长度为1到 \(k\) 的第一次出现的位置。长度为 \(p\) 第一次出现的位置更新为 \(t + p - 1\) 。
因此直接用数组维护就好啦!
蒟蒻码
点击查看代码
#include<bits/stdc++.h>
const int N = 1e6 + 7;
int n, f[N], now;
// f[i] : 记录联通块大小为 i 的第一次出现的位置
// now : 记录现在的连通块大小
long long ans, sum;
// ans : 记录答案
// sum : 目前这个左端点的答案
char s[N];
int main() {
scanf("%d%s", &n, s + 1);
for(int i = 1; i <= n; i++) f[i] = n + 1;
for(int i = n; i >= 1; i--) {
if(s[i] - '0') now++, sum += f[now] - i; // 联通块大小++, 计算比左端点为 i + 1 的贡献多了多少
else while(now) f[now] = i + now, now--; // 一个连通块的结束,更新 f 的值
ans += sum;
}
printf("%lld\n", ans);
return 0;
}
CF1428G1 Lucky Numbers (Easy Version)
蒟蒻语
这题没有压行就成Hard Version最短代码解了(
要知道这题那么 \(sb\) 就不啃 \(D\) 和 \(E\) 了。
蒟蒻解
首先有一个非常简单但是错误的多重背包的想法:
让分拆出来的 \(k\) 个数中,每一个数在十进制下每一位都是0,3,6或9,于是对于第 \(x\) 位把 \(3k\) 个大小为 \(3 \times 10^{x}\) ,价值为 \(F_{x}\) 的物品丢进多重背包里面,然后输出答案。
这样子显然是不对的,例如输入的数不是3的倍数就被卡掉了。因为还可能在某一位上价值是0。然后考虑贪心,我们肯定要让这些位置上不是0,3,6,9的位置越少越好。
有一个很显然的结论:一定可以让某一位上价不是0,3,6,9的个数减少到1。证明:如果有两个非0,3,6,9的数 \(a\) 和 \(b\) 。如果 \(a + b > 9\) ,那么可以变成9和 \(a + b - 9\) ;否则可以变成0和 \(a + b\) 。
那么我们只要对这不是0,3,6,9的那些位置进行特殊处理即可。为了方便,我们把这些位放在同一个数上。可以对于这些数提前统计他们的价值。然后对于剩下 \(k - 1\) 个数,按照前面所提到的错误做法,对于第 \(x\) 位把 \(3(k - 1)\) 个大小为 \(3 \times 10^{x}\) ,价值为 \(F_{x}\) 的物品丢进多重背包里面。但是这样子会TLE,然后改成二进制优化多重背包即可。不会二进制优化背包?毙了吧
蒟蒻码
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define L(i, j, k) for(int i = (j); i <= (k); i++)
#define R(i, j, k) for(int i = (j); i >= (k); i--)
#define ll long long
const int N = 1e6 + 7;
int n, m, k, sz, t, q;
ll p[6], f[N];
void Push(int v, ll w) { R(i, 1e6, v) f[i] = max(f[i], w + f[i - v]); }
void gg(int v, int w) {
int now = min(k, (int)1e6 / v);
for(int i = 1; i < now; i <<= 1) now -= i, Push(v * i, 1ll * w * i);
Push(v * now, 1ll * w * now);
}
int main() {
scanf("%d", &k), sz = 1, k = 3 * (k - 1);
L(i, 0, 5) scanf("%d", &p[i]);
L(i, 0, 1e6) {
int now = 0, x = i, s = x % 10;
while(x) {
if(s % 3 == 0) f[i] += 1ll * p[now] * (s / 3);
x /= 10, ++now, s = x % 10;
}
}
L(i, 0, 5) gg(sz * 3, p[i]), sz *= 10;
scanf("%d", &q);
while(q--) scanf("%d", &t), printf("%lld\n", f[t]);
return 0;
}
[P5336 CF1437G Death DBMS
蒟蒻语
这题感觉不是很难,但是既然放在 EDU 的 G 题,那么还是写写题解吧。
蒟蒻解
首先看到 "子串",那么想到 ACAM 和 SAM。本篇题解就使用 ACAM。
然后我们先对于最开始给定的 n 个串建立一个 ACAM。
然后考虑对于每一个串在 ACAM 上对应的位置赋上这个串的值。
查询其实就是在 fail 树上查询一些节点到根的最大值。
这个其实就是要求在 fail 树上单点修改,求链上最大值。这个东西树剖很好维护。
然后注意以下一个细节:一个串可能出现多次。这个 multiset 维护一下最大值就好了
蒟蒻码
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define L(i, j, k) for(int i = (j), i##E = (k); i <= i##E; i++)
#define R(i, j, k) for(int i = (j), i##E = (k); i >= i##E; i--)
#define ll long long
#define db double
#define mp make_pair
const int N = 3e5 + 7;
const int M = N * 4;
const int inf = 1e9;
int n, m, endid[N], VAL[N];
int ch[N][26], fa[N], tot = 1;
multiset<int> st[N];
int insert(char *s, int n) {
int now = 1;
L(i, 0, n - 1) {
if(!ch[now][s[i] - 'a']) ch[now][s[i] - 'a'] = ++tot;
now = ch[now][s[i] - 'a'];
}
return now;
}
void bfs() {
queue<int> q;
L(i, 0, 25) if(ch[1][i]) fa[ch[1][i]] = 1, q.push(ch[1][i]); else ch[1][i] = 1;
while(!q.empty()) {
int u = q.front();
q.pop();
L(i, 0, 25) {
int v = ch[u][i];
if(!v) ch[u][i] = ch[fa[u]][i];
else fa[v] = ch[fa[u]][i], q.push(v);
}
}
}
int head[N], edge_id;
struct node { int to, next; } e[N << 1];
void add_edge(int u, int v) {
++edge_id, e[edge_id].next = head[u], e[edge_id].to = v, head[u] = edge_id;
}
int siz[N], maxto[N], dep[N], uid[N], idtot, heavy[N];
void dfs1(int x) {
siz[x] = 1;
for(int i = head[x]; i; i = e[i].next) {
int v = e[i].to;
fa[v] = x, dep[v] = dep[x] + 1, dfs1(v), siz[x] += siz[v];
if(siz[v] > siz[heavy[x]]) heavy[x] = v;
}
}
void dfs2(int x) {
uid[x] = ++idtot;
if(heavy[x]) maxto[heavy[x]] = maxto[x], dfs2(heavy[x]);
for(int i = head[x]; i; i = e[i].next) {
int v = e[i].to;
if(v == heavy[x]) continue;
maxto[v] = v, dfs2(v);
}
}
int maxn[M];
void build(int x, int l, int r) {
maxn[x] = -1;
if(l == r) return;
int mid = (l + r) / 2;
build(x << 1, l, mid), build(x << 1 | 1, mid + 1, r);
}
void add(int id, int L, int R, int wz, int val) {
// if(id == 1) cout << wz << " is : " << val << endl;
if(L == R) return maxn[id] = val, void();
int mid = (L + R) / 2;
if(wz <= mid) add(id << 1, L, mid, wz, val);
else add(id << 1 | 1, mid + 1, R, wz, val);
maxn[id] = max(maxn[id << 1], maxn[id << 1 | 1]);
}
int query(int id, int L, int R, int l, int r) {
if(l <= L && R <= r) return maxn[id];
int mid = (L + R) / 2, res = -1;
if(l <= mid) res = max(res, query(id << 1, L, mid, l, r));
if(r > mid) res = max(res, query(id << 1 | 1, mid + 1, R, l, r));
// if(id == 1) cout << l << " to " << r << "'s max = " << res << endl;
return res;
}
int get(int x) {
int res = -1;
while(x) res = max(res, query(1, 1, tot, uid[maxto[x]], uid[x])), x = fa[maxto[x]];
return res;
}
char s[N];
int main() {
scanf("%d%d", &n, &m);
L(i, 1, n) scanf("%s", s), endid[i] = insert(s, strlen(s));
bfs();
L(i, 2, tot) add_edge(fa[i], i);
dfs1(1), maxto[1] = 1, dfs2(1);
build(1, 1, tot);
L(i, 1, n) add(1, 1, tot, uid[endid[i]], 0), st[endid[i]].insert(0);
while(m--) {
int opt, x, val;
scanf("%d", &opt);
if(opt == 1) {
scanf("%d%d", &x, &val);
int now = endid[x];
st[now].erase(st[now].lower_bound(VAL[x]));
st[now].insert(val), VAL[x] = val;
add(1, 1, tot, uid[now], *st[now].rbegin());
}
else {
int maxn = -1, now = 1;
scanf("%s", s);
L(i, 0, strlen(s) - 1) now = ch[now][s[i] - 'a'], maxn = max(maxn, get(now));
printf("%d\n", maxn);
}
}
return 0;
}
CF830D Singer House
蒟蒻语
蒟蒻解
首先考虑dp维护题目要求的深度为 \(i,\) 每个节点最多经过一次的不同有向路径数量 \(f_{i}\) 。
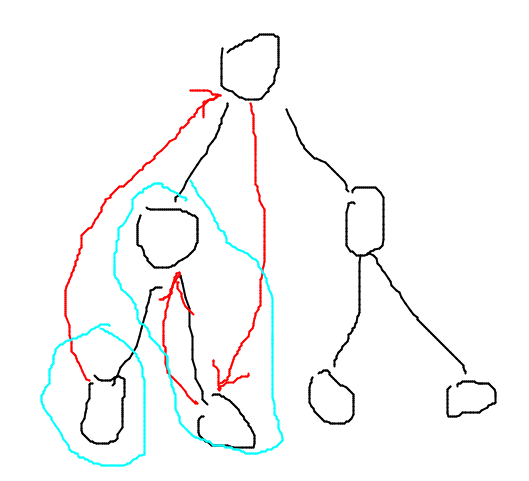
明显的,只维护这个东西是不对的,因为忽视了这样的情况:

这样子这条路径是由原来的被蓝色圈圈包住的两个部分转移而来。
那么考虑记录 \(g_{i}\) 为两条不相交的有向路径数量。
然后蓟翊兴冲冲地去尝试了,并过了前两个样例,但是过不了第三个样例,这是为什么?
发现 \(g_{i}\) 也有可能是由三条不相交的有向路径转移而来!
那么正解就浮出水面了:维护深度为 \(i, j\) 条不相交的有向路径数量 \(dp_{i,j}\) 。
转移如果想明白了状态其实很简单。这里还是说一下。
首先用背包求出深度为 \(i - 1\) ,和为 \(j\) 条不相交的有向路径数量:bb[j] += dp[i - 1][k] * dp[i - 1][j - k]
第一种转移:根结点独立,然后其他的路径让两个子树自由组合:dp[i][j] += bb[j - 1] + 2 * dp[i - 1][j - 1]
第二种转移:路径不包括根结点,或根结点为路径起点或终点:dp[i][j] += (2 * j + 1) * bb[j] + (4 * j + 2) * dp[i - 1][j]
第三种转移:路径包括根结点,且连接两条原来在子树中是两条链:dp[i][j] += j * (j + 1) * bb[j + 1] + 2 * j * (j + 1) * dp[i - 1][j + 1]
时间复杂度 \(O(n^{3})\) ,可以卷积劣化到 \(O(n^{2}\log n)\) ,空间复杂度 \(O(n^{2})\) ,可以滚动数组优化到 \(O(n)\) 。
蒟蒻码
点击查看代码
#include<bits/stdc++.h>
#define L(i, j, k) for(int i = j; i <= k; i++)
#define R(i, j, k) for(int i = j; i >= k; i--)
using namespace std;
const int N = 444;
const int mod = 1e9 + 7;
int n, dp[N][N], bb[N];
int main() {
scanf("%d", &n);
dp[1][1] = 1;
L(i, 2, n) {
fill(bb, bb + n + 1, 0);
L(j, 1, n) L(k, 0, j) (bb[j] += 1ll * dp[i - 1][k] * dp[i - 1][j - k] % mod) %= mod;
dp[i][1] = 1;
L(j, 1, n) {
int t = 0;
(dp[i][j] += (2ll * j + 1) * bb[j] % mod) %= mod;
(dp[i][j] += (4ll * j + 2) % mod * dp[i - 1][j] % mod) %= mod;
(dp[i][j] += 1ll * j * (j + 1) % mod * bb[j + 1] % mod) %= mod;
(dp[i][j] += 2ll * j * (j + 1) % mod * dp[i - 1][j + 1] % mod) %= mod;
(dp[i][j] += bb[j - 1] % mod) %= mod;
(dp[i][j] += 2ll * dp[i - 1][j - 1] % mod) %= mod;
}
}
printf("%d\n", dp[n][1]);
return 0;
}
CF1062E Company
蒟蒻语
蒟蒻解
数据结构学傻的蒟蒻来写一个新思路
这题的正解是利用多个结点的 \(lca\) 是 \(df\) s 序最大的结点和 \(df\) s 序最小的结点的 \(lca\) 。但是这里考虑如何不用这种方法。
首先用线段树合并处理出在每一个结点的子树里面的点。
答案分为两种情况:
- 包含结点 \(l\) 。
那么我们可以以 \(l\) 为起点向上跳。找到第一个大小 \(\geq r - l\) 的结点 \(p\) 。然后在结点 \(p\) 上面二分找到是没有选哪个结点。
- 包含除了结点 \(l\) 外的所有结点。
那么我们可以以 \(l\) 为起点向上跳。找到第一个大小 \(\geq r - l\) 的结点 \(p\) 。这样子的答案就是 \(l\) 。
蒟蒻码
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define L(i, j, k) for(int i = (j), i##E = (k); i <= i##E; i++)
#define R(i, j, k) for(int i = (j), i##E = (k); i >= i##E; i--)
#define ll long long
#define db double
#define mkp make_pair
const int N = 2e5 + 7;
const int M = 8e6 + 7;
int n, m, fa[N], siz[N], dep[N], jp[20][N];
int head[N], edge_id;
int hd[N], sum[M], ch[M][2], tot;
struct node { int to, next; } e[N << 1];
void add_edge(int u, int v) { ++edge_id, e[edge_id].next = head[u], e[edge_id].to = v, head[u] = edge_id; }
void add(int &x, int L, int R, int wz) {
if(!x) x = ++tot;
sum[x]++;
if(L == R) return;
int mid = (L + R) / 2;
if(wz <= mid) add(ch[x][0], L, mid, wz);
else add(ch[x][1], mid + 1, R, wz);
}
int merge(int x, int y) {
if(!x || !y) return x | y;
int nw = ++tot;
sum[nw] = sum[x] + sum[y];
ch[nw][0] = merge(ch[x][0], ch[y][0]);
ch[nw][1] = merge(ch[x][1], ch[y][1]);
return nw;
}
int query(int x, int L, int R, int l, int r) {
if(!x) return 0;
if(l <= L && R <= r) return sum[x];
int mid = (L + R) / 2, res = 0;
if(l <= mid) res += query(ch[x][0], L, mid, l, r);
if(r > mid) res += query(ch[x][1], mid + 1, R, l, r);
return res;
}
void dfs(int x) {
siz[x] = 1, add(hd[x], 1, n, x);
for(int i = head[x]; i; i = e[i].next) {
int v = e[i].to;
dep[v] = dep[x] + 1, dfs(v), siz[x] += siz[v];
// cout << " ? \n";
hd[x] = merge(hd[x], hd[v]);
// cout << " ! \n";
}
}
int get(int x, int l, int r, int y) {
int nowans = query(hd[x], 1, n, l, r);
if(nowans > y) return 0;
if(nowans == y) return x;
int now = x;
R(i, 18, 0) if(jp[i][now] && query(hd[jp[i][now]], 1, n, l, r) < y) now = jp[i][now];
now = fa[now];
if(query(hd[now], 1, n, l, r) != y) return 0;
return now;
}
int main() {
scanf("%d%d", &n, &m);
L(i, 2, n) scanf("%d", &fa[i]), add_edge(fa[i], i), jp[0][i] = fa[i];
L(i, 1, 18) L(j, 1, n) jp[i][j] = jp[i - 1][jp[i - 1][j]];
dfs(1);
while(m--) {
int l, r;
scanf("%d%d", &l, &r);
int resa = get(l + 1, l + 1, r, r - l), resb = get(l, l, r, r - l);
// 1 : not contain l
if(dep[resa] >= dep[resb]) printf("%d %d\n", l, dep[resa]);
// 2 : contain l
else {
int L = l, R = r;
while(L < R) {
int mid = (L + R) / 2;
if(query(hd[resb], 1, n, L, mid) != mid - L + 1) R = mid;
else L = mid + 1;
}
printf("%d %d\n", L, dep[resb]);
}
}
return 0;
}
P5279 [ZJOI2019] 麻将
蒟蒻语
这题非常的神啊。。。
蒟蒻解
首先考虑如何判定一副牌是否是“胡”的。
不要想着统计几个值 \(O(1)\) 算,可以考虑复杂度大一点的。
首先先把 7 个对子的状态判掉。然后考虑 4 个面子和 1 个对子的情况。
记录一个 \(dp_{i,j,k}\) : \(i\) 表示现在有没有留出对子, \(j\) 表示现在形如 \(i, i - 1\) 的牌的多余的个数, \(k\) 表示现在形如 \(i\) 的牌对的个数, 整个状态的值表示在这种情况下产生的面子数量的最大值。
使用dp套dp,对于这个 \(dp_{i,j,k}\) 分别是多少给压缩起来。这个状态以及转移可以 \(bfs\) 找。
最后进行一个期望 \(dp\) , \(f_{i,j,k}\) 表示算了前 \(i\) 种牌,现在总共有 \(j\) 个牌,目前是第 \(j\) 个 \(dp\) 状态的方案数。最后拆贡献,对于每一个 \(j\) 算有多少概率还会继续加牌。
蒟蒻码
点击查看代码
#include<bits/stdc++.h>
#define L(i, j, k) for(int i = j, i##E = k; i <= i##E; i++)
#define R(i, j, k) for(int i = j, i##E = k; i >= i##E; i--)
#define ll long long
#define ull unsigned long long
#define db double
#define pii pair<int, int>
#define mkp make_pair
using namespace std;
const int N = 405;
const int M = 2200;
const int mod = 998244353;
int qpow(int x, int y) {
if(x == 0) return 0;
int res = 1;
for(; y; x = 1ll * x * x % mod, y >>= 1) if(y & 1) res = 1ll * res * x % mod;
return res;
}
int ny(int x) { return qpow(x, mod - 2); }
int n, winid, ans;
int max(int a, int b) { return a > b ? a : b; }
void Max(int &a, int b) { a = max(a, b); }
struct DPAM {
int f[3][3];
void clear() { L(i, 0, 2) L(j, 0, 2) f[i][j] = -1; }
};
DPAM operator + (DPAM aa, int bb) {
DPAM res; res.clear();
L(i, 0, 2) L(j, 0, 2) if(aa.f[i][j] != -1)
L(k, 0, 2) if(bb >= i + j + k) Max(res.f[j][k], min(aa.f[i][j] + i + (bb - i - j - k) / 3, 4));
return res;
}
void FMAX(DPAM &aa, DPAM bb) {
L(i, 0, 2) L(j, 0, 2) Max(aa.f[i][j], bb.f[i][j]);
}
struct node {
int cnt; DPAM dp[2];
void clear() { cnt = 0; dp[0].clear(), dp[1].clear(); }
};
node win() { node res; res.clear(), res.cnt = 114514; return res; }
bool check(node aa) {
if(aa.cnt >= 7) return 1;
L(i, 0, 2) L(j, 0, 2) if(aa.dp[1].f[i][j] >= 4) return 1;
return 0;
}
bool operator < (node aa, node bb) {
L(t, 0, 1) L(i, 0, 2) L(j, 0, 2) if(aa.dp[t].f[i][j] ^ bb.dp[t].f[i][j]) return aa.dp[t].f[i][j] < bb.dp[t].f[i][j];
return aa.cnt < bb.cnt;
}
node operator + (node aa, int bb) {
if(aa.cnt == 114514) return aa;
node res;
res.clear(), res.cnt = aa.cnt + (bb >= 2);
FMAX(res.dp[0], aa.dp[0] + bb);
FMAX(res.dp[1], aa.dp[1] + bb);
if(bb >= 2) FMAX(res.dp[1], aa.dp[0] + (bb - 2));
if(check(res)) return win();
return res;
}
int tot, dp[2][N][M];
map<node, int> mp;
int G[M][5], jc[N], njc[N];
int C(int x, int y) { return 1ll * jc[x] * njc[x - y] % mod * njc[y] % mod; }
void bfs() {
queue<node> q;
node gg;
gg.clear(), gg.cnt = 0, gg.dp[0].f[0][0] = 0;
mp[gg] = ++tot, q.push(gg);
while(!q.empty()) {
node u = q.front(); int id = mp[u];
q.pop();
L(i, 0, 4) {
node v = u + i;
if(!mp.count(v)) {
G[id][i] = mp[v] = ++tot, q.push(v);
if(v.cnt == 114514) winid = tot;
}
else G[id][i] = mp[v];
}
}
}
int cnt[N];
void work() {
dp[0][0][1] = 1;
L(i, 1, n) {
int now = (i & 1);
memset(dp[now], 0, sizeof(dp[now]));
L(j, 1, tot) L(k, 0, (i - 1) * 4) L(t, 0, 4 - cnt[i])
(dp[now][k + t][G[j][t + cnt[i]]] += 1ll * dp[now ^ 1][k][j] * C(4 - cnt[i], t) % mod) %= mod;
}
L(i, 0, n * 4 - 13) L(j, 1, tot) if(j != winid) (ans += 1ll * ny(C(4 * n - 13, i)) * dp[n & 1][i][j] % mod) %= mod;
}
int mian() {
bfs();
scanf("%d", &n);
jc[0] = njc[0] = 1;
L(i, 1, n * 4) jc[i] = 1ll * jc[i - 1] * i % mod, njc[i] = ny(jc[i]);
L(i, 1, 13) {
int x, y;
scanf("%d%d", &x, &y), cnt[x]++;
}
work();
printf("%d\n", ans);
return 0;
}
CF611H New Year and Forgotten Tree
蒟蒻语
不过怎么证明那个结论是对的啊,蒟蒻思考了好久还是不懂,求解 /kel
蒟蒻解
提供一种新思路。
首先考虑如何判断一个状态是否合法。
考虑把所有十进制长度一样的数缩成一个点。
这样的点的个数 ≤5。
蒟蒻猜了一个结论:只要满足对于所有缩出来的点的子集的点的个数 > 子集内边的个数,那么就是有解的。
这时 SegmentTree 会下凡告诉你:这是对的!卡不掉!
但是这样只能判断可不可行啊,不能输出方案啊。。。
发现这个东西判断的时间复杂度很小,可以多次判断。
那么我们可以删叶子,对于每一种边尝试一下可不可以删,然后连边(在原图上,让最后每一个长度只剩下一个点,剩下的特殊处理)。
蒟蒻码
点击查看代码
#include<bits/stdc++.h>
#define L(i, j, k) for(int i = j, i##E = k; i <= i##E; i++)
#define R(i, j, k) for(int i = j, i##E = k; i >= i##E; i--)
#define ll long long
#define db double
#define pii pair<int, int>
#define mkp make_pair
using namespace std;
const int N = 100;
const int M = 2e6 + 7;
const int inf = 1e9;
int n, m, mx, p[N], minn[N], D[M][2], sum = 0;
int a[N][N];
bool check() {
L(t, 0, (1 << mx) - 1) {
int ds = 0, bs = 0;
L(i, 1, mx) if(t & (1 << (i - 1))) ds += p[i];
if(!ds) continue;
L(i, 1, mx) if(t & (1 << (i - 1))) L(j, 1, mx) if(t & (1 << (j - 1))) bs += a[i][j];
if(bs >= ds) return 0;
}
return 1;
}
int Cnt(int x) { return x == 0 ? 0 : Cnt(x / 10) + 1; }
char sa[N], sb[N];
bool get() {
L(x, 1, mx) L(i, 1, mx) if(a[x][i]) {
if(p[x] > 1) {
a[x][i] --, p[x] --;
if(check()) return printf("%d %d\n", minn[x] + p[x], minn[i]), 1;
a[x][i] ++, p[x] ++;
}
if(p[i] > 1) {
a[x][i] --, p[i] --;
if(check()) return printf("%d %d\n", minn[x], minn[i] + p[i]), 1;
a[x][i] ++, p[i] ++;
}
}
return 0;
}
int main() {
scanf("%d", &n), mx = Cnt(n);
L(i, 1, n) p[Cnt(i)]++;
minn[1] = 1;
L(i, 2, mx) minn[i] = minn[i - 1] * 10;
L(i, 1, n - 1) scanf("%s%s", sa, sb), D[i][0] = strlen(sa), D[i][1] = strlen(sb), a[D[i][0]][D[i][1]] ++;
if(!check()) return puts("-1"), 0;
while(get()) sum ++;
L(x, 1, mx) L(i, 1, mx) if(a[x][i]) printf("%d %d\n", minn[x] + p[x] - 1, minn[i] + p[i] - 1), sum ++ ;
if(sum != n - 1) assert(0);
return 0;
}
CF1458D Flip and Reverse
蒟蒻语
来菜园采菜啊
\(T\) 组询问,每次给定一个字符串,每次可以选择一个1和0数量相等的字符串,然后把字符串前后翻转并01翻转。求最后得到的字典序最小的字符串。
数据范围: \(T,n\leq 5\times 10^{5},\sum n\leq 5\times 10^{5}\)
蒟蒻解
刚才有个群友问我乙菜鸡发生肾摸事了,我说怎么回事?给我发了几张CF分数对比图,我一看!嗷!原来是昨天,我打了一场CF,爆零了,掉分到newbie,又被嘲讽了。
首先假设我们有一个 \(x\) 值,遇到 0,让 \(x\) 减少 1;遇到 1 让 \(x\) 增加 1。
考虑按照原字符串建立一张图。对于每一个 \(x\) 值建立一个点。例如说现在的 \(x\) 值为 \(t\) , 遇到了一个 1, 然后我们从 \(t\) 到 \(t + 1\) 连一条无向边。
选择一个1和0数量相等的字符串,前后的x值一定相等。于是这就形成了一个环。
考虑将这个字符串取反,其实相当于从这个点绕着这个环走一圈。
然后我们要求的是这张图的最小字典序的欧拉路径。
可以考虑贪心,能向小的数走就往小数的走。
怎么判定数 \(t\) 能不能往小数 \(t - 1\) 走?首先一定要有 \(t\) 到 \(t - 1\) 的这条边,如果 \(t\) 有到 \(t + 1\) 的边那么 \(t\) 到 \(t - 1\) 的边数至少为 2(肯定要返回 \(t\) )。
时间复杂度 \(O(\sum n)\)
蒟蒻码
点击查看代码
#include<bits/stdc++.h>
#define L(i, j, k) for(int i = j, i##E = k; i <= i##E; i++)
#define R(i, j, k) for(int i = j, i##E = k; i >= i##E; i--)
#define ll long long
#define ull unsigned long long
#define db double
#define pii pair<int, int>
#define mkp make_pair
using namespace std;
const int N = 5e5 + 7;
const int inf = 1e9 + 7;
int n, cnt[N << 1];
char s[N];
void Main() {
scanf("%s", s + 1), n = strlen(s + 1);
int now = 0;
L(i, 1, n) {
if(s[i] == '1') cnt[N + now] ++, now ++;
else now --, cnt[N + now] ++;
}
now = 0;
L(i, 1, n) {
if(cnt[N + now - 1] > 0 && (!cnt[N + now] || cnt[N + now - 1] > 1)) --now, cnt[N + now] --, putchar('0');
else cnt[N + now] --, now ++, putchar('1');
}
puts("");
L(i, -n, n) cnt[N + i] = 0;
}
int main() {
int T; scanf("%d", &T);
while(T--) Main();
return 0;
}
P5043 【模板】树同构([BJOI2015]树的同构)
蒟蒻语
蒟蒻解
听说题解里全是 \(O\left(n^{2} m\right)\) 的, 今天神 @hehezhou 介绍了一种优秀的方法。
用多项式哈希,记录走过的结点的顺序。
首先如果是有根树,而且儿子结点有先后遍历顺序这样子就是对的。
然后如果儿子结点没有顺序就按照儿子的哈希值排序,然后再哈希。
有根树拓展到无根树只要找到重心然后再做即可。(两个重心也是可以的,比较的时候看看两个哈希值能否对应上即可)
于是得出了哈希值,最后暴力比较即可。
时间复杂度 \(\Theta (mn\log n)\) ,时间复杂度瓶颈再于对哈希值排序。
神仙 Forever_Pursuit 说他用基数排序,因此是 \(\Theta(mn)\) 。
蒟蒻码
点击查看代码
#include<bits/stdc++.h>
#define L(i, j, k) for(int i = j, i##E = k; i <= i##E; i++)
#define R(i, j, k) for(int i = j, i##E = k; i >= i##E; i--)
#define ll long long
#define ull unsigned long long
#define db double
#define pii pair<int, int>
#define pil pair<int, lonf long>
#define mkp make_pair
using namespace std;
const int N = 55;
const int mod = 1019260817;
const int G = 19491001;
int Pow[N];
int n, m;
struct Tree {
int A, B;
} f[N];
bool operator == (Tree aa, Tree bb) {
return aa.A == bb.A && aa.B == bb.B;
}
int head[N], edge_id;
struct edge {
int to, next;
} e[N << 1];
void add_edge(int u, int v) {
++edge_id, e[edge_id].to = v, e[edge_id].next = head[u], head[u] = edge_id;
}
int has[N], siz[N], dep[N], rt, rrt, rtm;
void findrt(int x, int fa) {
siz[x] = 1;
int maxn = 0;
for(int i = head[x]; i; i = e[i].next) {
int v = e[i].to;
if(v == fa) continue;
findrt(v, x), siz[x] += siz[v], maxn = max(maxn, siz[v]);
}
maxn = max(maxn, n - siz[x]);
if(maxn < rtm) rtm = maxn, rt = x, rrt = 0;
else if(maxn == rtm) rrt = x;
}
int tot;
pii sav[N];
void dfs(int x, int fa) {
has[x] = 1ll * dep[x] * Pow[1] % mod, siz[x] = 1;
for(int i = head[x]; i; i = e[i].next) {
int v = e[i].to;
if(v == fa) continue;
dep[v] = dep[x] + 1, dfs(v, x);
}
tot = 0;
for(int i = head[x]; i; i = e[i].next) {
int v = e[i].to;
if(v == fa) continue;
sav[++tot] = mkp(has[v], siz[v]);
}
sort(sav + 1, sav + tot + 1);
L(i, 1, tot) (has[x] += 1ll * sav[i].first * Pow[siz[x]] % mod) %= mod, siz[x] += sav[i].second;
}
void In(int x) {
rtm = mod, rrt = 0;
scanf("%d", &n);
L(i, 1, n) {
int v; scanf("%d", &v);
if(v) add_edge(i, v), add_edge(v, i);
}
findrt(1, -1);
dep[rt] = 1, dfs(rt, -1), f[x].A = has[rt];
if(rrt) dep[rrt] = 1, dfs(rrt, -1), f[x].B = has[rrt];
if(f[x].A < f[x].B) swap(f[x].A, f[x].B);
L(i, 1, n) head[i] = 0;
edge_id = 0;
}
int mian() {
Pow[0] = 1;
L(i, 1, 50) Pow[i] = 1ll * Pow[i - 1] * G % mod;
scanf("%d", &m);
L(i, 1, m) In(i);
L(i, 1, m) L(j, 1, i) if(f[i] == f[j]) {
printf("%d\n", j);
break;
}
return 0;
}
CF1466G Song of the Sirens
蒟蒻语
蒟蒻解
SAM学傻了,看到子串,直接把Hash解决的问题用SAM做了,于是成功没调出来 \(100+\) 行的代码。让 \(s_{l,r}\) 表示 \(s\) 的第 \(l\) 个字符到第 \(r\) 个字符形成的串,len \((s)\) 表示 \(s\) 的字符串长度。
考虑对于一个串 \(s_i\) 对 \(\boldsymbol{\varpi}\) 的贡献,要么是从 \(s_{i - 1}\) 中得到的,要么是从跨越 \(t_i\) 的子串中得到的。
跨越 \(t_i\) 的贡献就是 \(s_{len(s) - len(w) + 2, len(s)} t_i s_{1, len(w) - 1}\) 中 \(w\) 出现的次数。这个可以 hash 解决。
设在 \(s_i\) 中跨越 \(t_i\) 的贡献是 \(g_i\) (特别的,在 \(s_0\) 中就是整个串的贡献),那么答案就是 \(\sum_{i=0}^{d} 2^{d-i} g_i\)
于是只要暴力这样做 \(+hash\) ,就得到了一个 \(\sum len(w_i)\times k_i\) 的算法。
然后考虑有很多重复的计算:如果 \(s_i\) 和 \(s_j\) 长度都比 \(w\) 长度大,而且 \(t_i = t_j\) ,那么他们跨越 \(t_i\) 的贡献是相同的!
那么可以考虑先计算前几个 \(s_i\) 对 \(\boldsymbol{w}\) 的贡献直到 \(s_i\) 的长度大于 \(\boldsymbol{w}\) ,然后后面贡献,对于每一个字符的答案是一样的,按照最开始的哈希方法处理以下即可。
显然这个哈希也可以用KMP来代替。
代码还是很好写的。
蒟蒻码
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define L(i, j, k) for(int i = (j), i##E = (k); i <= i##E; i++)
#define R(i, j, k) for(int i = (j), i##E = (k); i >= i##E; i--)
#define ll long long
#define db double
#define mkp make_pair
const int N = 2e6 + 7;
const int tN = 1e5 + 7;
const int mod = 1e9 + 7;
const int p = 1019260817;
const int G = 19491001;
const int inv2 = (mod + 1) / 2;
int n, Q, has[N], Len, sPow[N];
void Init(string s) { Len = s.size(); L(i, 1, Len) has[i] = (has[i - 1] + 1ll * (s[i - 1] - 'a' + 1) * sPow[i] % p) % p; }
int d[tN];
string g[tN], s[23], ms, t, now;
int calc(int x) {
int nowlen = g[x].size(), Hs = 0, res = 0;
L(i, 1, nowlen) (Hs += 1ll * (g[x][i - 1] - 'a' + 1) * sPow[i] % p) %= p;
L(i, 0, Len - nowlen) res += (has[i + nowlen] - has[i] + p) % p == 1ll * Hs * sPow[i] % p;
return res;
}
int tmp, maxn;
int Pow[N], iPow[N], ans[tN];
int qz[tN][26];
int main() {
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin >> n >> Q;
cin >> s[0] >> t;
Pow[0] = iPow[0] = sPow[0] = 1;
L(i, 1, n) Pow[i] = Pow[i - 1] * 2 % mod, iPow[i] = 1ll * iPow[i - 1] * inv2 % mod;
L(i, 1, 2000001) sPow[i] = 1ll * sPow[i - 1] * G % p;
L(i, 1, Q) cin >> d[i] >> g[i], maxn = max(maxn, (int)g[i].size());
now = s[0], Init(s[0]);
L(i, 1, Q) (ans[i] += 1ll * Pow[d[i]] * calc(i) % mod) %= mod;
int tmp = 0;
while(1) {
if((int)s[tmp].size() > maxn) break;
L(i, 1, Q) if(d[i] > tmp) {
ms.clear();
int tlen = min((int)s[tmp].size(), (int)g[i].size() - 1);
L(_i, (int)s[tmp].size() - tlen, (int)s[tmp].size() - 1) ms.push_back(s[tmp][_i]);
ms.push_back(t[tmp]);
L(_i, 0, tlen - 1) ms.push_back(s[tmp][_i]);
Init(ms);
(ans[i] += 1ll * Pow[d[i] - tmp - 1] % mod * calc(i) % mod) %= mod;
}
s[tmp + 1] = s[tmp] + t[tmp] + s[tmp], ++tmp;
}
// 计算了前 tmp 位
L(i, 1, n) {
L(j, 0, 25) qz[i][j] = qz[i - 1][j];
(qz[i][t[i - 1] - 'a'] += iPow[i]) %= mod;
}
int Len = now.size();
L(i, 1, Q) {
if(d[i] <= tmp) continue;
int orz = g[i].size() - 1;
L(j, 0, 25) {
ms.clear();
L(_i, (int)s[tmp].size() - orz, (int)s[tmp].size() - 1) ms.push_back(s[tmp][_i]);
ms.push_back(j + 'a');
L(_i, 0, orz - 1) ms.push_back(s[tmp][_i]);
Init(ms);
(ans[i] += 1ll * (qz[d[i]][j] - qz[tmp][j] + mod) % mod * Pow[d[i]] % mod * calc(i) % mod) %= mod;
}
}
L(i, 1, Q) printf("%d\n", ans[i]);
return 0;
}
CF1266F Almost Same Distance
蒟蒻语
蒟蒻解
看到其他题解里面全是什么 bfs 序上线段树啊,什么根号的奇怪东西啊,蒟蒻用一个非常好写的 O(n) 做法(这里实现的时候用了 vector,所以比较慢),写篇题解来造福社会
目前在 cf 上是最短解
如果 \(k = 1\) ,答案是 \(\max (deg_i + 1)\)
考虑有3个点的情况:

洛谷
通过放缩法可以证明(证明比较简单而繁琐略去)。考虑在这种情况下的链长(图中的 \(a, b, c\) ):
- \(k\) 为奇数:有一个中心结点,旁边的链最多只有一个长为 \(\frac{k - 1}{2}\) 的,其他都是 \(\frac{k + 1}{2}\) 。
- \(k\) 为偶数:有一个中心结点,旁边的都是长为 \(\frac{k}{2}\) 的链。
但是这样会发现在样例2挂掉了。漏掉了下面的情况:

因此有了第3种情况:在 \(k\) 为偶数的时候,有两个中心结点,旁边链长要求为 \(\frac{k}{2}\) 。
在这3种情况下,我们发现一定满足 \(ans_{x} \geq ans_{x+2}\) 。
对于前两个情况,每一个结点我们记录以他为根时的子树深度,然后把这个深度进行排序。 \(k\) 为偶数时第 \(i\) 大数 \(t\) 的则表示 \(ans_{2t} \geq i\) 。奇数稍微麻烦点,第 \(i\) 大数 \(t\) 的则表示 \(ans_{2t-1} \geq i\) ,如果不和排在前面的数相同,那么我们发现长度为 \(ans_{2t+1} \geq i\) (用这条链和之前面的几条链放在一起,就是长度为 \(t\) 和一堆 \(t+1\) )。这里都很显然。
第3种情况,显然可以把所有相邻的两个位置 \(A, B\) 的子树深度数组给合并在一起,然后再按照第一种情况做就行了,可惜是 \(n^2\) 的。
考虑从后到前,对于这个子树深度数组扫描线,扫到 \(k\) 时更改每一个数的时候判一下和相邻结点的点的和sum-2(sum会算到 \(B\) 做 \(A\) 子树和 \(A\) 做 \(B\) 子树的贡献,因此sum要减2)是否可以更新 \(\text{ans}_k\) 。
这个可以套路地看作是计算父亲结点和子树结点的最大值,额外记录一下子树sum的最大值 \(m \times s\) ,在修改一个结点的时候更新父亲结点的 \(m \times s\) ,同时用 \(\max (sum_{fa}, mxs)\) 来更新答案。
具体实现时,第1和第2种情况也可以把排序换成扫描线做到 \(O(n)\)
蒟蒻码
点击查看代码
#include<bits/stdc++.h>
#define L(i, j, k) for(int i = j, i##E = k; i <= i##E; i++)
#define R(i, j, k) for(int i = j, i##E = k; i >= i##E; i--)
using namespace std;
const int N = 5e5 + 7;
void Max(int &x, int y) { if(x < y) x = y; }
int n, deg[N], Fa[N], f1[N], f2[N], sum[N], mx1[N], mx2[N], up[N], mxs[N], las, u, v;
vector<int> G[N], e[N];
void dfs1(int x) {
Max(f1[0], deg[x] + 1), mxs[x] = -1e9;
for(int v : e[x]) if(v ^ Fa[x]) {
Fa[v] = x, dfs1(v);
if(mx1[v] + 1 > mx1[x]) mx2[x] = mx1[x], mx1[x] = mx1[v] + 1; else Max(mx2[x], mx1[v] + 1);
}
}
void dfs2(int x) {
if(x ^ 1) G[up[x]].push_back(x);
for(int v : e[x]) if(v ^ Fa[x]) G[mx1[v] + 1].push_back(x);
for(int v : e[x]) if(v ^ Fa[x]) up[v] = max(up[x], mx1[v] + 1 == mx1[x] ? mx2[x] : mx1[x]) + 1, dfs2(v);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n, f1[n] = f2[n] = 1;
L(i, 1, n - 1) cin >> u >> v, deg[u] ++, deg[v] ++, e[u].push_back(v), e[v].push_back(u);
dfs1(1), dfs2(1);
R(i, n, 1) {
las = 0;
for(int t : G[i]) {
sum[t] ++, Max(mxs[Fa[t]], sum[t]);
Max(f2[i], sum[t] + mxs[t] - 2), Max(f2[i], sum[t] + sum[Fa[t]] - 2); // case 3
Max(f2[i], sum[t]); // case 1
Max(f1[i - 1], sum[t]); // case 2
if(las != t) Max(f1[i], sum[t]); las = t; // case 2
}
}
R(i, n, 1) Max(f1[i - 1], f1[i]), Max(f2[i - 1], f2[i]);
L(i, 1, n) cout << (i % 2 ? f1[i / 2] : f2[i / 2]) << " ";
cout << endl;
return 0;
}
CF1483F Exam
蒟蒻语
来 cnblogs 里看
给定 \(n\) 个不同的字符串 \(S_{1}, S_{2}, \ldots, S_{n}\) ,求数对 \((i, j)\) 的个数,满足 \(S_{i}\) 是 \(S_{j}\) 的子串,且不存在一个不等于 \(i\) 和 \(j\) 的 \(k\) ,满足 \(S_{i}\) 是 \(S_{k}\) 的子串且 \(S_{k}\) 是 \(S_{j}\) 的子串。
数据范围: \(n,\sum |S|\leq 10^6\)
蒟蒻解
我还是学傻了啊,经过神sjy的提醒才发现在这儿ACAM和SAM是等价的。
考虑枚举长的字符串,短的字符串必然在长的字符串中出现。
枚举短串的右端点,对答案有贡献的字符串一定是左端点最靠左边的。
然后还要求没有其他的字符串包含这个字符串,可以简单地判掉。
可以结合这张图理解

但是这样会算重,如何解决?
发现只有算到的次数 = 在长串中出现的次数的情况对答案有 1 的贡献。
算到的次数可以轻松维护,在长串中出现的次数可以用树状数组 + ACAM 来维护。时间复杂度和空间复杂度都是 \(\Theta((\sum |S|) \log (\sum |S|))\) 。
蒟蒻码
点击查看代码
#include<bits/stdc++.h>
#define L(i, j, k) for(int i = j, i##E = k; i <= i##E; i++)
#define R(i, j, k) for(int i = j, i##E = k; i >= i##E; i--)
#define ll long long
#define pii pair<int, int>
#define x first
#define y second
#define sz(a) ((int) (a).size())
using namespace std;
const int N = 1e6 + 7;
template<typename T> inline void cmax(T &x, T y) { if(x < y) x = y; }
template<typename T> inline void cmin(T &x, T y) { if(y < x) x = y; }
using namespace std;
int ns, cnt[N], tot, fa[N];
vector< int > change[N], e[N], qet[N];
int ch[N][26], sz[N];
void ad(int x, int y) {
for(; x <= tot + 1; x += (x & -x)) sz[x] += y;
}
int query(int x) {
int res = 0;
for(; x; x -= (x & -x)) res += sz[x];
return res;
}
int qry(int l, int r) {
return query(r) - query(l - 1);
}
int n, m, siz[N], hv[N], St[N], En[N], idtot, mx[N], sx[N], lef[N], sG[N];
void dfs(int x) {
St[x] = ++idtot;
for(int v : e[x]) {
if(!sx[v]) sx[v] = sx[x];
mx[v] = max(mx[v], mx[x]), dfs(v);
}
En[x] = idtot;
}
void ins(string s) {
int now = 0;
L(i, 0, sz(s) - 1) {
if(!ch[now][s[i] - 'a']) ch[now][s[i] - 'a'] = ++tot;
now = ch[now][s[i] - 'a'];
}
}
void build() {
queue<int> q;
L(i, 0, 25) if(ch[0][i]) q.push(ch[0][i]);
while(!q.empty()) {
int u = q.front();
q.pop();
L(i, 0, 25)
if(ch[u][i]) fa[ch[u][i]] = ch[fa[u]][i], q.push(ch[u][i]);
else ch[u][i] = ch[fa[u]][i];
}
}
string s[N];
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> n;
L(i, 1, n) cin >> s[i], ins(s[i]);
L(i, 1, n) {
int now = 0;
L(j, 0, sz(s[i]) - 1) now = ch[now][s[i][j] - 'a'], change[now].push_back(i);
cmax(mx[now], sz(s[i])), sx[now] = now;
}
build();
L(i, 1, tot) e[fa[i]].push_back(i);
dfs(0);
L(i, 1, n) {
L(j, 1, sz(s[i])) qet[j].clear();
int now = 0;
L(j, 0, sz(s[i]) - 1) {
now = ch[now][s[i][j] - 'a'], ad(St[now], 1);
if(j == sz(s[i]) - 1) now = fa[now];
lef[j] = j - mx[now] + 1, sG[j] = sx[now];
}
lef[sz(s[i])] = 1e9;
R(j, sz(s[i]) - 1, 0) {
if(lef[j] <= j && lef[j] < lef[j + 1]) qet[j - lef[j] + 1].push_back(sG[j]);
lef[j] = min(lef[j], lef[j + 1]);
}
L(j, 1, sz(s[i])) {
for(int x : qet[j]) cnt[x] ++;
for(int x : qet[j]) if(cnt[x]) ns += (qry(St[x], En[x]) == cnt[x]),
cnt[x] = 0;
}
now = 0;
L(j, 0, sz(s[i]) - 1) now = ch[now][s[i][j] - 'a'], ad(St[now], -1);
}
cout << ns << "\n";
return 0;
}
CF1514E Baby Ehab's Hyper Apartment
蒟蒻语
能在场上想出来自己不怎么擅长的交互题还是比较开心的
但是因为不了解 Extra Registration(在 30 分钟之后就不能报名了),没能交上去...
给定一张 \(n\) 个点竞赛图, 你可以进行一些询问, 询问有两种:
- \(1a b\) : 查询是否有从 \(a\) 到 \(b\) 的有向边。这种询问次数 \(\leqslant 9n\) 。
- \(2xks_1s_2\ldots s_k\) :查询 \(\pmb{x}\) 到 \(s_1,s_2,\dots ,s_k\) 是否存在一条有向边。这种询问次数 \(\leq 2n\) 。
最后要求输出对于所有 \((i,j)\) , 是否有 \(i\) 到 \(j\) 的路径。多测。
蒟蒻解
因为把竞赛图缩点之后形成的强联通分量是一条链,如果知道了这些强联通分量就可以得出答案。
接下来分成两个步骤:
- 找到一条包括 \(1,2,\ldots ,n\) 的路径。
- 在这条路径上进行缩点。
步骤1
考虑增量,设这条链原先是 \(v_{1}, v_{2}, \ldots, v_{k}\) ,现在要加入点 \(k\) 。
因此要找出一个位置 \(p\) ( \(1 \leq p \leq k + 1\) )满足有一条从 \(v_{p-1}\) 到 \(k\) 的边且有一条从 \(k\) 到 \(v_p\) 的边,并在 \(p\) 之前插入 \(k\) 。
发现如果有从 \(v_{l-1}\) 到 \(k\) 的边且有从 \(k\) 到 \(v_r\) 的边,那么可以在 \([l, r]\) 找到答案。
考虑二分答案,如果有 \(k\) 到 \(v_{mid}\) 的边,那么在 \([l, mid]\) 中可以找到答案,否则在 \([mid + 1, r]\) 中可以找到答案。
需要 \(n\log n\) 个询问1。
步骤2
设目前缩出来的链是 \(S_{1}\rightarrow S_{2}\rightarrow \dots \rightarrow S_{k}\)
从后往前缩点,对于一个 \(S_{t}\) 中的点 \(z\) ,如果存在一条从 \(z\) 到 \(S_{1}, S_{2}, \ldots, S_{t-1}\) 中的点的边,那么 \(S_{t}\) 和 \(S_{t-1}\) 必然在一个集合中。
不停地这样缩点即可得到最终答案。需要 \(2n\) 个询问 2。
蒟蒻码
点击查看代码
#include<bits/stdc++.h>
#define L(i, j, k) for(int i = j, i##E = k; i <= i##E; i++)
#define R(i, j, k) for(int i = j, i##E = k; i >= i##E; i--)
#define ll long long
#define pii pair<int, int>
#define db double
#define x first
#define y second
#define ull unsigned long long
#define sz(a) ((int) (a).size())
#define vi vector<int>
using namespace std;
const int N = 233;
int n, tot, v[N];
set < int > S[N];
void merge(int x, int y) {
for(int k : S[y]) S[x].insert(k);
S[y].clear();
}
int getin() {
int k;
return cin >> k, k;
}
bool check(int x, int y) {
return cout << 1 << " " << x << " " << y << endl, getin();
}
bool all[N][N], vis[N];
int rmain() {
memset(all, 0, sizeof(all)), memset(vis, 0, sizeof(vis)), memset(v, 0, sizeof(v));
L(i, 1, tot) S[i].clear();
tot = 0;
cin >> n;
L(i, 0, n - 1) {
int l = 1, r = tot + 1;
while(l < r) {
int mid = (l + r) >> 1;
if(mid == tot + 1 || check(i, v[mid])) r = mid;
else l = mid + 1;
}
R(i, tot, l) v[i + 1] = v[i];
++tot, v[l] = i;
}
L(i, 1, tot) S[i].insert(v[i]);
int now = tot;
while(now > 1) {
for(int v : S[now]) if(!vis[v]) {
cout << 2 << " " << v << " ";
int cnt = 0;
L(i, 1, now - 1) cnt += sz(S[i]);
cout << cnt << " ";
L(i, 1, now - 1) for(int u : S[i]) cout << u << " ";
cout << endl;
if(getin()) {
merge(now - 1, now);
break;
}
vis[v] = true;
}
--now;
}
L(i, 1, tot) L(j, i, tot) for(int u : S[i]) for(int v : S[j]) all[u][v] = true;
cout << 3 << endl;
L(i, 0, n - 1) {
L(j, 0, n - 1) cout << all[i][j];
cout << endl;
}
return getin(), 0;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int T;
cin >> T;
while(T--) rmain();
return 0;
}
P7722 [Ynoi2007] tmpq
蒟蒻解
首先这个问题太诡异了,我们把问题看作可以对 \(a, b, c\) 都单点修改。要求 \(i < j < k\) 的 \(b_i = a_j = c_k\) 的对数。
考虑对于 \(b_{i} = a_{j} = c_{k} = w\) 的 \(w\) 进行根号分治。考虑 \(w\) 在 \(a, b, c\) 中的总出现次数。
- 对于出现了 \(< B\) 次的数,每次对这个数进行修改的时候暴力 DP,在 \(k\) 处加即可。
- 对于出现了 \(\geq B\) 次的数, 这样的数只有 \(\Theta\left(\frac{n + q}{B}\right)\) 个。所以对于每个数维护个动态 DP 即可。
取 \(B = \Theta (\sqrt{n + q})\) ,这两种情况都容易平衡到单次 \(\Theta (\sqrt{n + q})\) ,所以这种做法时间复杂度是 \(\Theta (q\sqrt{n + q})\) 。
目前是 Luogu 最优解。
P8351 [SDOI/SXOI2022] 子串统计
蒟蒻语
题出的好!难度不适中,覆盖知识点广,题目又着切合实际的背景,解法比较自然。
给出题人点赞 !
给定长度为 \(n\) 的字符串 \(s\) 。你有一个字符串 \(t = s\) ,你每次操作可以在前面或在后面删除一个字符,直到字符串中只有一个字符。设每次操作后得到的字符串分别是 \(a_1, a_2, \ldots, a_{n-1}\) ,那么这种操作的权值就是 \(\prod_{1 \leq i < n} \operatorname{occ}(a_i)\) 。其中 \(\operatorname{occ}(a)\) 表示字符串 \(a\) 在 \(s\) 中的出现次数。求对于所有操作序列的权值和。
数据范围: \(n\leq 10^5\)
蒟蒻解
首先考虑一下有哪些本质不同的串,满足从左边或右边删除一个字符,能使得在整个串中出现的次数变大了。称这样的串为“好串”。
不妨仅考虑从左删除一个字符,有多少出现次数变了:只有parent tree的节点 \(x\) 上,长度恰好为 \(maxlen_{fa_x} + 1\) 的串。因此满足这种条件的串只有 \(\Theta (n)\) 个。
我们把“好串”和“好串”从前或从后删除一个字符后得到的串称为“关键串”。我们已经知道了出现次数不同的串之间的转移了,因此现在我们只用关心出现次数相同的关键串之间的转移了。
我们只关心每个串第一次出现时的位置。由于每个串在整个串中出现的次数相同,因此这样做,串间的包含关系不变。
接下来我们就可以写一份暴力了,可以直接树状数组暴力枚举每个串 \([l,r]\) 的子串 \([x,y]\) ,从 \([l,r]\) 走到 \([x,y]\) 的权值是 \(\binom{x-l+r-y}{x-l}c^{r-l+1}c^{-(y-x)}\) 。这样可以拿到40分。
考虑优化。我们显然可以把 \(c^{r - l + 1}c^{-(y - x)}\) 直接在两个区间处直接处理掉,因此我们就只用考虑从 \([l,r]\) 走到 \([x,y]\) 的方案数了。
直接算方案数很难算,我们不妨先打个表看看关键串出现的位置有没有什么规律:

可以发现,对于每种颜色的每一块,围成的区域很规整。可以看作是一个长度为 \(m\) 的序列 \(a\) 满足 \(a_{i} \leq a_{i+1}\) ,表示有 \(i\) 列,第 \(i\) 列从上到下有连续 \(a_{i}\) 个元素。
为什么是这个形状的呢?首先容易发现如果一个点下面和右边都在连通块内,那么这个点也在连通块内。
其次就是这个图形满足只有一个点是“极点”的(也就是满足上面和右边都不在连通块内),这个可以考虑如果存在两个,这两个同时包含串 \(t\) ,而这两个串不相交,说明串 \(t\) 的出现次数并不一样。因此就只有一个“极点”了。
接下来考虑怎么求解。我们要从右上角的元素转移到左下角边界上的元素。这个东西可以用类似 gym102978J 的分治算法,每次取出 mid 划分,中间用 4 次卷积转移,然后分裂成两个问题。具体如下图:

P8351 [SDOI/SXOI2022] 子串统计
蒟蒻语
蒟蒻解
蒟蒻码
点击查看代码
P8351 [SDOI/SXOI2022] 子串统计
蒟蒻语
蒟蒻解
蒟蒻码
点击查看代码
P8351 [SDOI/SXOI2022] 子串统计
蒟蒻语
蒟蒻解
蒟蒻码
点击查看代码



 浙公网安备 33010602011771号
浙公网安备 33010602011771号