【ZJOI2017】线段树

题目描述

线段树是九条可怜很喜欢的一个数据结构，它拥有着简单的结构、优秀的复杂度与强大的功能，因此可怜曾经花了很长时间研究线段树的一些性质。

最近可怜又开始研究起线段树来了，有所不同的是，她把目光放在了更广义的线段树上：在正常的线段树中，对于区间 $[l, r]$，我们会取 $m = \lfloor \frac{l+r}{2} \rfloor$，然后将这个区间分成 $[l, m]$ 和 $[m + 1, r]$ 两个子区间。在广义的线段树中，$m$ 不要求恰好等于区间的中点，但是 $m$ 还是必须满足 $l \le m < r$ 的。不难发现在广义的线段树中，树的深度可以达到 $O(n)$ 级别。

例如下面这棵树，就是一棵广义的线段树：

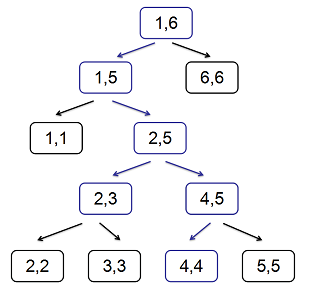
sigmoid

为了方便，我们按照先序遍历给线段树上所有的节点标号，例如在上图中，$[2, 3]$ 的标号是 $5$，$[4, 4]$ 的标号是 $9$，不难发现在 $[1, n]$ 上建立的广义线段树，它共有着 $2n − 1$ 个节点。

考虑把线段树上的定位区间操作（就是打懒标记的时候干的事情）移植到广义线段树上，可以发现在广义的线段树上还是可以用传统的线段树上的方法定位区间的，例如在上图中，蓝色节点和蓝色边就是在定位区间 $[2, 4]$ 时经过的点和边，最终定位到的点是 $[2, 3]$ 和 $[4, 4]$。

如果你对线段树不熟悉，这儿给出定位区间操作形式化的定义：给出区间 $[l, r]$，找出尽可能少的区间互不相交的线段树节点，使得它们区间的并集恰好是 $[l, r]$。

定义 $S_{[l,r]}$ 为定位区间 $[l, r]$ 得到的点集，例如在上图中，$S_{[2,4]} = \{5, 9\}$。定义线段树上两个点 $u, v$ 的距离 $d(u, v)$ 为线段树上 $u$ 到 $v$ 最短路径上的边数，例如在上图中 $d(5, 9) = 3$。

现在可怜给了你一棵 $[1, n]$ 上的广义的线段树并给了 $m$ 组询问，每组询问给出三个数 $u, l, r (l \le r)$，可怜想要知道 $\sum_{v \in S_{[l, r]}} d(u, v)$。

输入格式

第一行输入一个整数 $n$。

接下来一行包含 $n - 1$ 个空格隔开的整数：按照标号递增的顺序，给出广义线段树上所有非叶子节点的划分位置 $m$。不难发现通过这些信息就能唯一确定一棵 $[1, n]$ 上的广义线段树。

接下来一行输入一个整数 $m$。

之后 $m$ 行每行输入三个整数 $u, l, r(1 \le u \le 2n − 1, 1 \le l \le r \le n)$，表示一组询问。

输出格式

对于每组询问，输出一个整数表示答案。

样例一

限制与约定

测试点编号	$n$	$m$	其他约定
1	$\le 100$	$\le 100$	无
2	$\le 2 \times 10^5$	$\le 20$	无
3		$\le 2 \times 10^5$	$r = n$
4			$r = n$
5			$u = 1$
6			$u = 1$
7			无
8
9
10

对于 100% 的数据，保证 $n \ge 2, m \ge 1$。

时间限制：$2\texttt{s}$

空间限制：$512\texttt{MB}$

现在看来思路不是很难想啊.....但写起来像翔一样难受，细节这么多，拍一组改一组.....怪不得范老师在现场写挂了QAQ

分析

我们可以对区间询问$[l,r]$，用节点$l-1$和节点$r+1$去走，前者像$lca$走的过程中，记录路径上的右孩子，后者记录左孩子，那么得到的这些孩子，就是我们要的区间，具体的可以看一下下面这张图，从mls的视频中抠出来的

例如我们要查询的是黑竖线所包含的区间，那么蓝线就是走上去的路径，红色的点就是记录下的孩子，这些孩子就是要和$u$求距离的点

那么单点$x$和$u$的区里的求法就是$d_x+d_u-2*d_{lca(x,u)}$

显然，我们可以把所有的点合在一起做，即$dist=\sum d_x+num_x*d_u-2*\sum d_{lca(u,x)}$

$\sum d_x+num_x*d_u-2$，我们可以通过$O(n)$大力预处理一波得到

那么最后一个怎么办，我们可以根据上图中黄线所连接的上端点成为悬挂点，我们可以通过$lca(u,l-1)$和$lca(u,r+1)$的深度把链分成两段，在$lca$先的所有端点的$\sum d_{lca(u,x)}=num_x*d_lca$,，上半部分点的$lca$就是其悬挂点，则可以通过前面得到的预处理求得

还有最后一个问题是，$l=1$或者$r=n$的时候怎么办，大力特判一波

这道题目是一道完完整整的细节题啊QAQ

思路不难，调试起来还是有点略蛋疼啊.....

#include<cstdio>  
#include<iostream>  
#include<algorithm>  
#include<cstdlib>  
#include<cstring>
#include<string>
#include<climits>
#include<vector>
#include<cmath>
#include<map>
#include<set>
#define LL long long
 
using namespace std;
 
inline char nc(){
  static char buf[100000],*p1=buf,*p2=buf;
  if (p1==p2) { p2=(p1=buf)+fread(buf,1,100000,stdin); if (p1==p2) return EOF; }
  return *p1++;
}
 
inline void read(int &x){
  char c=nc();int b=1;
  for (;!(c>='0' && c<='9');c=nc()) if (c=='-') b=-1;
  for (x=0;c>='0' && c<='9';x=x*10+c-'0',c=nc()); x*=b;
}
 
inline void read(LL &x){
  char c=nc();LL b=1;
  for (;!(c>='0' && c<='9');c=nc()) if (c=='-') b=-1;
  for (x=0;c>='0' && c<='9';x=x*10+c-'0',c=nc()); x*=b;
}

inline int read(char *s)
{
	char c=nc();int len=0;
	for(;!(c>='A' && c<='Z');c=nc()) if (c==EOF) return 0;
	for(;(c>='A' && c<='Z');s[len++]=c,c=nc());
	s[len++]='\0';
	return len;
}

inline void read(char &x){
  for (x=nc();!(x>='A' && x<='Z');x=nc());
}

int wt,ss[19];
inline void print(int x){

	if (x<0) x=-x,putchar('-');
	if (!x) putchar(48); else {
	for (wt=0;x;ss[++wt]=x%10,x/=10);
	for (;wt;putchar(ss[wt]+48),wt--);}
}
inline void print(LL x){
	if (x<0) x=-x,putchar('-');
	if (!x) putchar(48); else {for (wt=0;x;ss[++wt]=x%10,x/=10);for (;wt;putchar(ss[wt]+48),wt--);}
}

int n,m,s,S,T1,T2,duan[200010],b[200010];
struct data
{
	int l,r,fa,d,c;
	LL rnum,rsum,lnum,lsum;
	vector<int> b;
}a[400010];
int p[400010][25];
struct tepan
{
	int id,x; 
}t1[400010],t2[400010];
 
void dfs(int u)
{
    a[u].c=1;
	for (int i=0;i<a[u].b.size();i++)
    {
        if (!a[a[u].b[i]].d)
        {
            a[a[u].b[i]].d=a[u].d+1;
            p[a[u].b[i]][0]=u;
            dfs(a[u].b[i]);
            a[u].c+=a[a[u].b[i]].c;
        }
    }
}

void pre(int x,int y)
{
	a[x].rsum=a[y].rsum;a[x].lsum=a[y].lsum;
	a[x].lnum=a[y].lnum;a[x].rnum=a[y].rnum;
	if (x==y+1) a[x].rnum++,a[x].rsum+=(LL)a[y].d;
	else a[x].lnum++,a[x].lsum+=(LL)a[y].d;
	if (a[x].l==a[x].r) return ;
	else pre(a[x].b[0],x),pre(a[x].b[1],x);
}
 
void init()
{
    for (int j=1;(1<<j)<=2*n-1;j++)
        for (int i=1;i<=2*n-1;i++)
            if (p[i][j-1]!=-1) p[i][j]=p[p[i][j-1]][j-1];
	for (int i=0;i<a[1].b.size();i++)
		pre(a[1].b[i],1);
}
 
int lca(int x,int y)
{
    if (a[x].d<a[y].d) swap(x,y);
    int i;
    for (i=0;(1<<i)<=a[x].d;i++);i--;
    for (int j=i;j>=0;j--)
        if (a[x].d-(1<<j)>=a[y].d) x=p[x][j];
    if (x==y) return x;
    for (int j=i;j>=0;j--)
        if (p[x][j]!=-1 && p[x][j]!=p[y][j])
            x=p[x][j],y=p[y][j];
    return p[x][0];
}
 
int Find(int x,int y)
{
    y=a[x].d-y;
    int i;
    for (i=0;(1<<i)<=a[x].d;i++);i--;
    for (int j=i;j>=0;j--)
        if (a[x].d-(1<<j)>=y) x=p[x][j];
    return x;
}

void build(int l,int r)
{
	S++;
	if (l==r) {b[l]=S;a[S].l=l,a[S].r=r;return ;}
	s++;a[S].l=l,a[S].r=r;
	int t=S,p=s;
	a[t].b.push_back(S+1);a[S+1].fa=t;
	build(l,duan[p]);
	a[t].b.push_back(S+1);a[S+1].fa=t;
	build(duan[p]+1,r);
}

LL calc(int x,int y,int z,int LCA)
{
	int t;LL res=0;
	if (y!=-1)
	{
		t=lca(x,y);
		if (a[t].d<a[LCA].d) res+=(a[y].rnum-a[a[LCA].b[0]].rnum)*a[t].d;
		else res+=(a[y].rnum-a[t].rnum)*a[t].d+a[t].rsum-a[a[LCA].b[0]].rsum;
		if (a[t].b.size()>0)if (lca(y,a[t].b[1])==t && a[t].d-1>=a[LCA].d && t!=x) res++;
	}
	if (z!=-1)
	{ 
		t=lca(x,z);
		if (a[t].d<a[LCA].d) res+=(a[z].lnum-a[a[LCA].b[1]].lnum)*a[t].d;
		else res+=(a[z].lnum-a[t].lnum)*a[t].d+a[t].lsum-a[a[LCA].b[1]].lsum;
		if (a[t].b.size()>0)if (lca(z,a[t].b[0])==t && a[t].d-1>=a[LCA].d && t!=x) res++;
	}
	return res;
}

void pan1(int x)
{
	t1[++T1].id=x,t1[T1].x=a[x].r;
	if (a[x].l==a[x].r) return ;
	pan1(a[x].b[0]);
}

void pan2(int x)
{
	t2[++T2].id=x,t2[T2].x=a[x].l;
	if (a[x].l==a[x].r) return ;
	pan2(a[x].b[1]);
}

void pre_tepan()
{
	T1=0;pan1(1);
	T2=0;pan2(1);
}

int Find1(int x)
{
	int l=1,r=T1,mid,res;
	while (l<=r)
	{
		mid=l+r>>1;
		if (t1[mid].x<=x) r=mid-1,res=mid;else l=mid+1;
	}
	return t1[res].id;
}

int Find2(int x)
{
	int l=1,r=T2,mid,res;
	while (l<=r)
	{
		mid=l+r>>1;
		if (t2[mid].x>=x) r=mid-1,res=mid;else l=mid+1;
	}
	return t2[res].id;
}

int main()
{
	read(n);
	for (int i=1;i<n;i++)
		read(duan[i]);
	s=0;S=0;
	build(1,n);
	a[1].d=1;dfs(1);
	init();
	pre_tepan();
	read(m);
	int x,y,z;
	while (m--)
	{
		read(x);read(y);read(z);
		LL res=0;int t;
		if (y==1 && z==n) print(a[1].d+a[x].d-2*a[1].d),puts("");
		else if (y==1)
		{
			y=Find1(z);
			t=lca(y,b[z+1]);
			res+=a[y].d+a[x].d-2LL*a[lca(x,y)].d;
			res+=a[b[z+1]].lsum-a[a[t].b[1]].lsum;
			res+=(a[b[z+1]].lnum-a[a[t].b[1]].lnum)*(LL)(a[x].d+1);
			res-=2LL*calc(x,-1,b[z+1],t);
			print(res),puts("");
		}
		else if (z==n)
		{
			z=Find2(y);
			t=lca(z,b[y-1]);
			res+=a[z].d+a[x].d-2LL*a[lca(x,z)].d;
			res+=a[b[y-1]].rsum-a[a[t].b[0]].rsum;
			res+=(a[b[y-1]].rnum-a[a[t].b[0]].rnum)*(LL)(a[x].d+1);
			res-=2LL*calc(x,b[y-1],-1,t);
			print(res),puts("");
		}
		else
		{ 
			t=lca(b[y-1],b[z+1]);
			res=a[b[y-1]].rsum-a[a[t].b[0]].rsum+a[b[z+1]].lsum-a[a[t].b[1]].lsum;
			res+=(a[b[y-1]].rnum-a[a[t].b[0]].rnum+a[b[z+1]].lnum-a[a[t].b[1]].lnum)*(LL)(a[x].d+1);
			res-=2LL*calc(x,b[y-1],b[z+1],t);
			print(res),puts("");
		}
	}
	return 0;
}

posted @ 2017-05-05 09:24 Xiejiadong 阅读(1419) 评论(0) 编辑收藏举报

刷新页面返回顶部

Xiejiadong

人生一场，何不放手一搏，但求青春无悔！

【ZJOI2017】线段树

题目描述

输入格式

输出格式

样例一

限制与约定

分析

公告