判断质数的几种方法

　　根据维基百科定义，质数（Prime number），又称素数，指在大于1的自然数中，除了1和此整数自身外，无法被其他自然数整除的数（也可定义为只有1和本身两个因数的数）。比1大但不是素数的数称为合数。1和0既非素数也非合数。质数在公钥加密算法（如RSA）中有重要的地位。

　　下边将会介绍几种较为常见的判断质/素数的方法：

　 1. 法一：最直接也最笨的方法

　　法一是按照质数的定义来考虑的，具体程序见下：

//*********************************** method 1 ***********************************//
bool IsPrime::isPrime_1(uint num)
{
    bool ret = true;
    for (uint i = 2; i < num - 1; i++)
    {
        if (num % i == 0)
        {
            ret = false;
            break;
        }
    }

    return ret;
}

　 2. 法二：将循环判断次数减少一半（大约）

　　对于一个正整数num而言，它对(num/2, num)范围内的正整数是必然不能够整除的，因此，我们在判断num的时候，没有必要让它除以该范围内的数。代码如下：

//*********************************** method 2 ***********************************//
bool IsPrime::isPrime_2(uint num)
{
    bool ret = true;
    uint ubound = num / 2 + 1;
    for (uint i = 2; i < ubound; i++)
    {
        if (num % i == 0)
        {
            ret = false;
            break;
        }
    }

    return ret;
}

　 3. 法三：在法二的基础上继续提高

　　对于一个小于num的正整数x，如果num不能整除x，则num必然不能整除num/x （num = num/x * x）。反之相同。我们又知num =√num*√num。 如果n除以大于√num的数，必得到小于√num的商，而小于√num的整数已经在2到√num的整数试过了，因为就没有必要再试（√num, num）范围内的数了。代码如下：

　　注：经常会看到别人说“一个数 n 如果是合数，那么它的所有的因子不超过sqrt(n)”。这句话是错误的。举一个例子，16的因子包括了1、2、4、8，但很明显8>√16。另外，因子跟因数是不一样的，因数还会包括数本身，如16的因数为1、2、4、8、16。

//*********************************** method 3 ***********************************//
bool IsPrime::isPrime_3(uint num)
{
    bool ret = true;
    uint ubound = sqrt(num) + 1;
    for (uint i = 2; i < ubound; i++)
    {
        if (num % i == 0)
        {
            ret = false;
            break;
        }
    }

    return ret;
}

　 4. 法四：考虑偶数的因素

　　我们都知道，除了2之外，其他所有的偶数（正整数）全都不是质数，因为它们都能被2整除。代码改进如下：

//*********************************** method 4 ***********************************//
bool IsPrime::isPrime_4(uint num)
{
    bool ret = true;
    if (num == 2)
        return ret;

    // it is no need to consider even numbers larger than 2
    if (num % 2 != 0)
    {
        uint ubound = sqrt(num) + 1;
        for (uint i = 2; i < ubound; i++)
        {
            if (num % i == 0)
            {
                ret = false;
                break;
            }
        }
    }
    else
    {
        ret = false;
    }

    return ret;
}

　 5. 法五：埃拉托斯特尼筛选法

　　当我们判断某个取值范围内的素数有哪些的时候，有一个方法非常可行，就是埃拉托斯特尼筛选法。这个算法效率很高，但占用空间较大。

　　我们知道，一个素数p只有1和p这两个约数，并且它的约数一定不大于其本身。因此，我们下边方法来筛选出来素数：

　　1）把从2开始的、某一范围内的正整数从小到大顺序排列；
　　2）剩下的数中选择最小的素数，然后去掉它的倍数。

　　3）依次类推，直到循环结束。

　　这种筛选法动态图如下：

　　

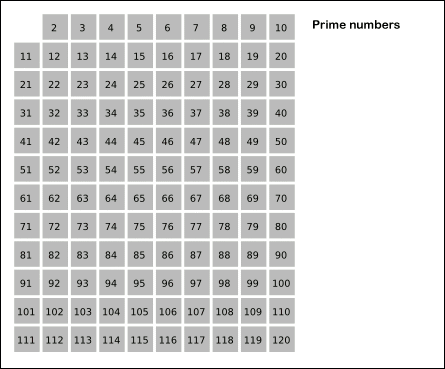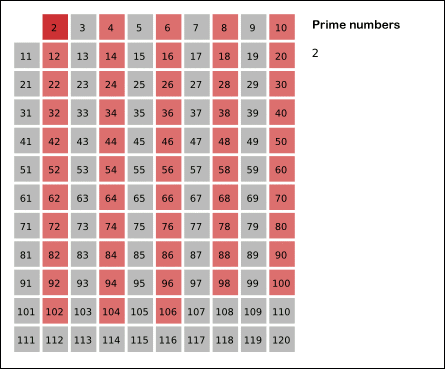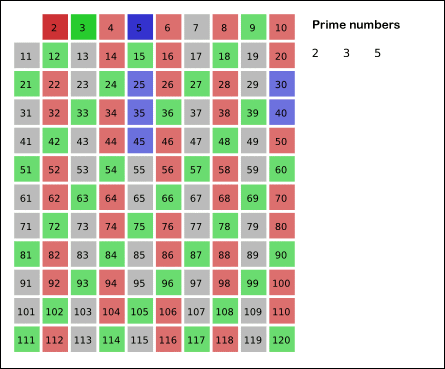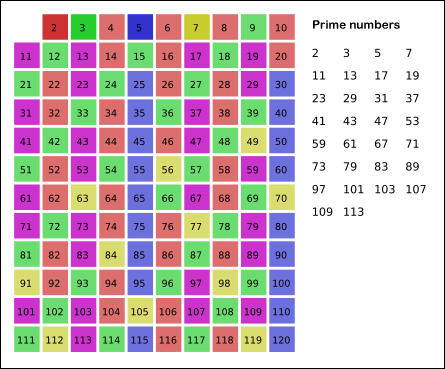
　　程序如下：

//*********************************** method 5 ***********************************//
// find prime numbers between [lower bound, upper bound)
vector<uint> IsPrime::retPrime_5(uint lbound, uint ubound)
{
    assert(lbound >= 0);
    assert(ubound >= 0);
    assert(lbound <= ubound);

    vector<bool> isprime;
    for (int i = 0; i < ubound; i++)
        isprime.push_back(true);

    for (int i = 2; i < ubound; i++)
    {
        for (int j = i + i; j < ubound; j += i)
        {
            isprime[j] = false;
        }
    }

    vector<uint> ret;
    for (int i = lbound; i < ubound; i++)
    {
        if (i != 0 && i != 1 && isprime[i])
            ret.push_back(i);
    }

    return ret;
}

 　6. 法六：去除法五中不必要的循环

　　对于法五来说，即使isprime中已经被判断为false的元素，它以及它的倍数还会被重新赋值为false（可能会有很多遍），而实际上已经没有必要这样子做。例如，第2个元素的倍数第4、6、8、10...个元素已经被判定为false，但循环到第4个元素的时候，第8、12、16...个元素还会被重新赋值，这有点重复。因此，我们要去掉这些重复的工作。代码比较简单，只需要加一语句即可，见下：

//*********************************** method 6 ***********************************//
// find prime numbers between [lower bound, upper bound)
vector<uint> IsPrime::retPrime_6(uint lbound, uint ubound)
{
    assert(lbound >= 0);
    assert(ubound >= 0);
    assert(lbound <= ubound);

    vector<bool> isprime;
    for (int i = 0; i < ubound; i++)
    {
        if (i < 2)
            isprime.push_back(false);
        else
            isprime.push_back(true);
    }

    for (int i = 2; i < ubound; i++)
    {
        if (isprime[i])
        {
            for (int j = i + i; j < ubound; j += i)
            {
                isprime[j] = false;
            }
        }
    }

    vector<uint> ret;
    for (int i = lbound; i < ubound; i++)
    {
        if (isprime[i])
            ret.push_back(i);
    }

    return ret;
}

　 7. 法七：大综合（结合法三及法六）

 　　法七是结合了法三及法六，代码如下：

//*********************************** method 7 ***********************************//
// find prime numbers between [lower bound, upper bound)
vector<uint> IsPrime::retPrime_7(uint lbound, uint ubound)
{
    assert(lbound >= 0);
    assert(ubound >= 0);
    assert(lbound <= ubound);

    vector<bool> isprime;
    for (int i = 0; i < ubound; i++)
    {
        if (i < 2)
            isprime.push_back(false);
        else
            isprime.push_back(true);
    }

    uint ulimit = sqrt(ubound) + 1;
    for (int i = 2; i < ulimit; i++)
    {
        if (isprime[i])
        {
            uint repeat = ubound / i;
            for (int j = 2; j < repeat; j++)
            {
                isprime[i * j] = false;
            }
        }
    }

    vector<uint> ret;
    for (int i = lbound; i < ubound; i++)
    {
        if (isprime[i])
            ret.push_back(i);
    }

    return ret;
}

 

　　整个程序代码（包括单元测试代码）见Github.

　　更多的方法请参见百度文库上的一篇文章。