CF2127游记
前言
CF2127 \(Div.1+Div.2\) 难度,场切 \(T1-T3\)
A.Mix Mex Max
题面
共 \(t\) 组数据,每组数据:
给定一个长度为 \(n\) 的数组,其中有一些未赋值的元素,标记为 \(-1\) 。
现在你需要确定是否存在一种赋值方式,使得:
\(\forall i,mex(a_i,a_{i+1},a_{i+2})=\max(a_i,a_{i+1},a_{i+2})+\min(a_i+a_{i+1}+a_{i+2})\)
思路
- 若 \(mex(a_i,a_{i+1},a_{i+2})=0\) 则一定有 \(a_i=a_{i+1}=a_{i+2}\)
- 若 \(mex(a_i,a_{i+1},a_{i+2})=k>0\) ,则一定有 \(a_i,a_{i+1},a_{i+2}\in{0,1,2,...,k-1}\) ,
而 \(\max(a_i,a_{i+1},a_{i+2})-\min(a_i,a_{i+1},a_{i+2})\le (k-1)-0=k-1<k\) 矛盾。
于是 \(mex(a_i,a_{i+1},a_{i+2})=0\) ,只需判断 \(a\) 中是否有 \(0\) ,以及 \(a\) 中有几种元素即可。
实现
#include<iostream>
using namespace std;
int t,n,x,y,flag;
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
cin>>t;
while(t--){
cin>>n;
x=-1;
flag=1;
for(int i=1;i<=n;++i){
cin>>y;
if(y!=-1){
if(x==-1)x=y;
else if(y!=x)flag=0;
}
}
if(flag&&x!=0)cout<<"YES\n";
else cout<<"NO\n";
}
return 0;
}
B.Hamiiid, Haaamid... Hamid?
题面
\(Alice\) 和 \(Bob\) 共进行 \(t\) 次游戏,每次游戏:
\(Bob\) 在有一个 \(n\) 个格子构成的走廊里,一些格子有墙壁,一个些格子是空着的。他们会在上面进行若干次操作:
每次操作,会发生两个事件:
- \(Alice\) 选择一个空格子在上面建一堵墙(不能是 \(Bob\) 在的格子)。
- \(Bob\) 选择一个方向,然后若该方向没有墙,则逃离走廊;否则他将击毁最近的墙壁并站在那个位置。
\(Alice\) 会选择最佳策略阻止 \(Bob\) ,求 \(Bob\) 最少需要多少天才能逃出走廊。
思路
非常简单的贪心。
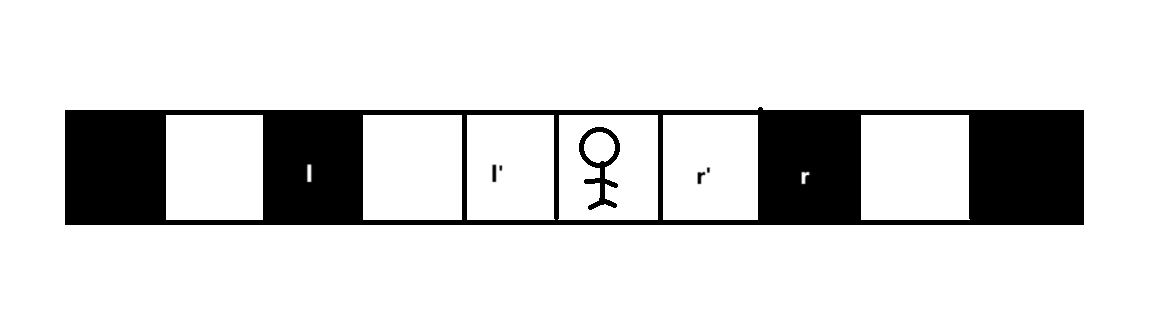
显然 \(Bob\) 只会向着一个方向破坏墙壁。
从 \(Bob\) 的位置向左右两端搜索,记 \(l,r\) 分别为两侧最近的墙壁到走廊边界的格子数,不难证明,从最近的墙壁开始破坏所需要最少的时间是 \(l,r\)。
然后 \(Alice\) 可以在 \(Bob\) 开始行动之前在他左右面前放一个墙壁,那么放完墙壁之后所需最少时间为 \(l',r'\) 。
那么答案为 \(\max(\min(l',r),\min(l,r'))\) 。
实现
#include<iostream>
using namespace std;
int t,n,x,l,r,fl,fr,ans;
string s;
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
cin>>t;
while(t--){
cin>>n>>x>>s;
s=" "+s+" ";
fl=s[x-1]=='.';
fr=s[x+1]=='.';
l=r=0;
for(int i=x-1;i>=1;--i)if(s[i]=='#'){l=i;break;}
for(int i=x+1;i<=n;++i)if(s[i]=='#'){r=n-i+1;break;}
ans=min(l,r)+1;
if(fl)ans=max(ans,min(x-1,r)+1);
if(fr)ans=max(ans,min(n-x,l)+1);
cout<<ans<<endl;
}
return 0;
}
C.Trip Shopping
题面
\(Alice\) 和 \(Bob\) 进行共 \(k\) 次游戏,每次游戏:
给定两个大小为 \(n\) 的数组 \(a,b\) ,进行 \(k\) 轮操作:
- \(Alice\) 选择 \(2\) 个引索 \(i,j\)
- \(Bob\) 将 \(a_i,a_j,b_i,b_j\) 任意排列。
\(\displaystyle v=\sum_i^n|a_i-b_i|\) 为游戏结果, \(Alice\) 希望最小化 \(v\) ,而 \(Bob\) 希望最大化 \(v\) 。
求最优情况下的花费。
思路
先将 \(a,b\) 调整为 \(a_i>b_i\) 。
显然, \(Alice\) 只会选择一对引索,因为每次选择一对引索, \(v\) 会只大不小。
那么我们只需要找到对应的那一组 \((i,j)\) 即可。
我们将 \((a_i,b_i)\) 抽象为数轴上的线段, \(v\) 即为线段的长度和。
那么对应的那一组即为间距最小的线段对,设其间距为 \(x\) ,那么 \(\Delta v=2\times\min(0,x)\) ,\(v=\Delta v+v_0\)。
我们按先 \(b\) 后 \(a\) 排序,贪心地依次遍历线段,即可得到其距离。
实现
#include<iostream>
#include<algorithm>
using namespace std;
#define ll long long
const int N=2e5+5;
int t,n,k,r;ll ans;
struct node{
int a,b;
bool operator < (const node t)const{
return (b^t.b)?a<t.a:b<t.b;
}
}p[N];
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
cin>>t;
while(t--){
cin>>n>>k;
for(int i=1;i<=n;++i)cin>>p[i].a;
for(int i=1;i<=n;++i){
cin>>p[i].b;
if(p[i].a<p[i].b)swap(p[i].a,p[i].b);
}
sort(p+1,p+1+n);
r=-1,ans=1e9+10;
for(int i=1;i<=n;++i){
if(r!=-1){
ans=min(ans,(ll)p[i].b-r);
r=max(r,p[i].a);
}
else r=p[i].a;
}
ans=max(0ll,ans);
ans*=2;
for(int i=1;i<=n;++i)ans+=p[i].a-p[i].b;
cout<<ans<<endl;
}
return 0;
}
另附
原来这一题是 \(Alice\) 和 \(Bob\) 轮流操作,求最优情况下的 \(v\)。
将会放到文章最后求解。
D.Root was Built by Love, Broken by Destiny
题面
共 \(t\) 组数据,每组数据:
给定 \(n\) 所房子,其分布在河的两岸,以及 \(m\) 座桥,将河对岸的两所房子 \(u_i,v_i\) 相连接。
求桥没有交叉的房子排列方案数 \(p\) 。
思路
记房子与桥形成的图为 \(G\)
我们需要先找到什么样的图 \(P_G\) 不为 \(0\) 。称 \(p_G=0\) 的 \(G\) 为无效的。
引理1
若 \(G\) 的子图 \(H\) 为无效的图,则 \(H\) 一定有桥相交或有桥连接了河同侧的房子。
故 \(G\) 一定也连接了河同侧的房子或有桥相交,即 \(G\) 也是无效的。
引理2
设 \(G\) 中包含任意长度的环。
我们不妨取其中只包含环的子图 \(H\) ,假设其是有效的。
我们取 \(H\) 中河北岸最左边的房子 \(u\) ,其必然连着河对岸的两个房子 \(L,R\) ( \(L\) 更靠左)。
那么考察 \(L\) ,其亦必然连接着河对岸的两个房子 \(u,v\) 。
而由于 \(u\) 是北岸最左侧的房子,所以 \(v\) 一定在 \(u\) 的右边。
则 \(u-R\) 桥会与 \(L-v\) 桥相交,与假设矛盾。
于是 \(H\) 是无效的,所以包含环的图 \(G\) 是无效的。
即有效的 \(G\) 一定是一棵树。
引理3
设 \(G\) 中有顶点拥有至少 \(3\) 个非叶邻居。
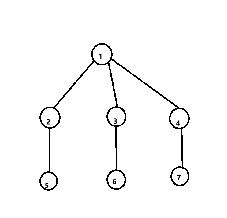
取其中如下的子图 \(H\) :
不妨假设 \(1\) 位于河北岸, \(2,3,4\) 依次排列于河南岸。
那么 \(5\)(\(7\)) 一定位于 \(1\) 的左(右)侧。
再考虑 \(6\) 节点,若其位于 \(1\) 左侧,则会有 \(1-2,3-6\) 交叉;
若位于 \(1\) 右侧,则会有 \(1-4,3-6\) 交叉。
于是 \(H\) 是无效的,所以包含环的图 \(G\) 是无效的。
\(G\) 去掉叶子节点后,所有节点的度数变为至多 \(2\) 所以其必定变为一条路径。
设 \(G\) 去掉叶子节点后的子图为 \(G'\)
- \(G'\) 为空。
那么 \(G\) 只有一条边,答案为 \(2\) 。 - \(G'\) 只有 \(1\) 个节点。
\(G\) 为一个星状图,答案取决于根节点在哪岸以及子节点的排列,答案为 \(2\times(n-1)!\) 。 - \(G'\) 为长度至少为 \(2\) 的路径。
\(G\) 关于河道翻转和东西翻转后方案不同。
于是答案为 \(\displaystyle 4\times\prod_{i\in S}(TS_i)!\) ,其中 \(TS_i\) 为 \(i\) 连接的叶子节点个数。
实现
#include<iostream>
using namespace std;
#define ll long long
const int N=2e5+5;
const ll mod=1e9+7;
int tt,n,m;
int f[N],nxt[N<<1],to[N<<1],cnt,deg[N];
bool vis[N],flag;
ll fac[N],ans;
void add(int u,int v){
++deg[u];
nxt[++cnt]=f[u];
f[u]=cnt;
to[cnt]=v;
}
void dfs0(int u,int fa){
vis[u]=1;
for(int i=f[u];i;i=nxt[i]){
if(to[i]==fa)continue;
if(vis[to[i]]){
flag=1;
return;
}
dfs0(to[i],u);
if(flag)return;
}
}
int main(){int x,y;
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
cin>>tt;
fac[0]=1;
for(int i=1;i<=2e5;++i)fac[i]=fac[i-1]*i%mod;
while(tt--){
cin>>n>>m;
flag=cnt=0;
for(int i=1;i<=n;++i)vis[i]=deg[i]=f[i]=0;
for(int i=1;i<=m;++i){
cin>>x>>y;
add(x,y);add(y,x);
}
if(n==2){
cout<<"2\n";continue;
}
dfs0(1,0);
if(flag){
cout<<"0\n";continue;
}
y=0;
for(int i=1;i<=n;++i){
y+=deg[i]>1;
x=0;
for(int j=f[i];j;j=nxt[j]){
x+=deg[to[j]]>1;
if(x>2){flag=1;break;}
}
if(flag)break;
}
if(flag)cout<<"0\n";
else if(y==1)cout<<2*fac[n-1]%mod<<endl;
else{
ans=4;
for(int u=1;u<=n;++u){
if(deg[u]==1)continue;
x=0;
for(int i=f[u];i;i=nxt[i])x+=deg[to[i]]==1;
ans=ans*fac[x]%mod;
}
cout<<ans<<endl;
}
}
return 0;
}
E.Ancient Tree
题面
共 \(t\) 组数据,每组数据:
给定一颗大小为 \(n\) 的树,以及一个正整数 \(k\) 。
树上每个节点有一种颜色 \(c_i\in[1,k]\) ,和权值 \(v_i\) 。
如果存在两个节点 \(l\) 和 \(r\) ,满足:
- \(lca(l,r)=v\)
- \(c_l=c_r\ne c_v\)
则称 \(v\) 为可爱节点。
定义一颗树的价值 \(v\) 为可爱节点的权值和。
现在树上有一些颜色褪去的节点 \(c_i=0\) ,需要你为他们染上颜色,并求最小的权值 \(v\) 。
思路
首先,我们会发现一些点无论其他的点如何染色,其一定是可爱节点。
所以答案至少是这些节点的权值和。
用于处理同一颜色的节点的 \(lca\) 我们可以通过虚树来处理。
我们为每个颜色建立一颗虚树,那么每个节点就会出现 \(3\) 种情况:
1.不属于任意一颗虚树;
2.属于 \(1\) 颗虚树;
3.属于至少 \(2\) 颗虚树。
显然, \(3.\) 节点一定是可爱节点。
那么我们每次 DFS 到未染色的节点 \(u\) 的时候,若:
- 其为 \(2.\) 节点:为其染上对应虚树颜色,这样其就不为可爱节点;
- 其为 \(3.\) 节点:为其染上任意对应虚树颜色,因为无论如何其均为可爱节点;
- 其为 \(1.\) 节点,且其子树中有含有颜色 \(c\) 的节点:为其染成颜色 \(c\) ,因为这样不会改变其祖先是否为可爱节点;
- 其为 \(1.\) 节点,且其字数中所有节点均无颜色:为其染成其父亲的颜色,这样也不会改变其祖先是否为可爱节点。
那么,最终答案即为所有 \(3.\) 节点的权值和。
实现
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
#define ll long long
#define max1(x,y) dfn[x]<dfn[y]?x:y
const int N=2e5+5,lgN=20;
int tt,n,k,w[N],c[N],cnt[N],col[N];
int dep[N],st[N][lgN],lg[N],dfn[N],DFN;
vector<int>g[N],cols[N],V;
bool mrk[N],cut[N];
void dfs0(int u,int ft){
st[dfn[u]=++DFN][0]=ft;
dep[u]=dep[ft]+1;
for(auto v:g[u]){
if(v==ft)continue;
dfs0(v,u);
}
}
void dfs1(int u,int cc){
if(c[u])cc=c[u];else c[u]=cc;
for(int v:g[u])if(v!=st[dfn[u]][0])dfs1(v,cc);
}
void init(){
for(int j=1;j<=lg[n];++j)
for(int i=1;i<=n-(1<<j)+1;++i)
st[i][j]=max1(st[i][j-1],st[i+(1<<j-1)][j-1]);
}
int lca(int x,int y){
if(x==y)return x;
if((x=dfn[x])>(y=dfn[y]))swap(x,y);
int d=lg[y-x++];
return max1(st[x][d],st[y-(1<<d)+1][d]);
}
void solve(){int x,y,L;bool flg=1;
cin>>n>>k;
DFN=0;
for(int i=1;i<=n;++i){
cin>>w[i];
g[i].clear();
col[i]=cnt[i]=cut[i]=0;
}
for(int i=1;i<=n;++i){
cin>>c[i];
if(c[i]){
flg=0;
cols[c[i]].push_back(i);
}
}
for(int i=1;i< n;++i){
cin>>x>>y;
g[x].push_back(y);
g[y].push_back(x);
}
if(flg){
cout<<"0\n";
for(int i=1;i<=n;++i)cout<<"1 ";
cout<<endl;
return;
}
dfs0(1,0);
init();
for(int i=1;i<=k;++i){
if(!cols[i].size())continue;
sort(cols[i].begin(),cols[i].end(),[&](int u,int v){
return dfn[u]<dfn[v];
});
for(int j=0;j<cols[i].size()-1;++j){
x=cols[i][j],y=cols[i][j+1],L=lca(x,y);
if(!mrk[L]){
if(c[L]){
if(c[L]!=i)cut[L]=1;
continue;
}
mrk[L]=1;
++cnt[L];
col[L]=i;
V.push_back(L);
}
}
for(auto v:V)mrk[v]=0;
V.clear();
cols[i].clear();
}
ll ans=0;
for(int i=1;i<=n;++i){
if(cut[i]||cnt[i]>1)ans+=w[i];
if(!c[i]&&cnt[i])c[i]=col[i];
}
for(int i=1;i<=n;++i)if(c[i]){dfs1(1,c[i]);break;}
cout<<ans<<endl;
for(int i=1;i<=n;++i)cout<<c[i]<<" ";
cout<<endl;
}
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
cin>>tt;
lg[0]=-1;for(int i=1;i<=2e5;++i)lg[i]=lg[i>>1]+1;
while(tt--)solve();
return 0;
}
后面几题难度有点高,我就等后面再写。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号