四小孩追逐问题及其拓展

四小孩追逐问题

有一个边长为 \(l\) 的正方形，四个顶点各有一个小孩，在运动过程中，小孩的速度始终向着其顺时针方向的下一个小孩，且大小始终为 \(v\) ，所有小孩碰到一起后运动结束，求时间。
对其中一个小孩分析

设小孩间距离为 \(x\)
则 \(dt\) 内两小孩距离的减少量为 $ dx = v_1 dt \times \cos 0 + v_2 dt \times \cos \frac{\pi}{2} =v_1 dt = v dt$
所以两小孩距离减少的速度为 \(v\) 。
又刚开始两小孩间距离为 \(l\) ，所以时间为 \(\frac{l}{v}\)

\(n\) 小孩追逐问题

有一个边长为 \(l\) 的正 \(n\) 边形，四个顶点各有一个小孩，在运动过程中，小孩的速度始终向着其顺时针方向的下一个小孩，且大小始终为 \(v\) ，所有小孩碰到一起后运动结束，求时间。
同上 \(dt\) 内两小孩距离的减少量为 \(dx = v_1 dt \times \cos 0 + v_2 dt \times \cos \frac{(n-2)\pi}{n}=v dt (1+\cos \frac{(n-2)\pi}{n})\)
则 \(t=\frac{l}{v(1+\cos \frac{(n-2)\pi}{n})}\)

平面追及问题

一条直线上有两个点，相距 \(l\) ，其中一个点沿着垂直于直线方向以 \(v_1\) 的速度运动，另一个点则以 \(v_2\) 的速度向着第一个点运动，求运动时间。
对某一时刻分析：

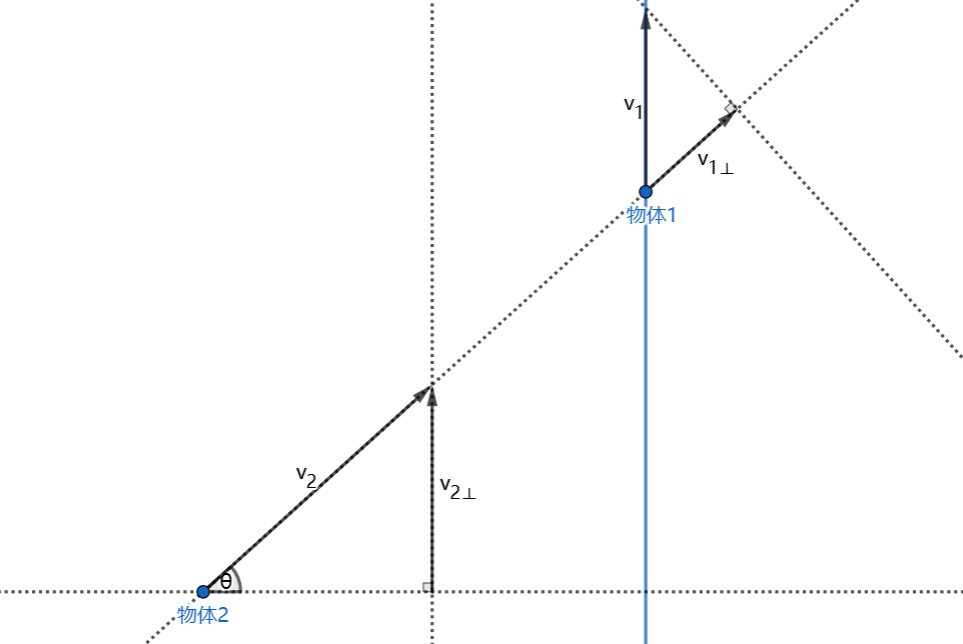
\(dt\) 内两者距离的减少量 $ dx = (v_2-v_{1\perp}) = ( v_2 - v_1 \times \sin \theta ) dt$
由定义： $ \displaystyle l=\int dx = \int (v_2-v_1\times \sin \theta) dt =v_2\int dt-v_1\int \sin \theta dt$
又两者最终相遇 \(\displaystyle \int v_{2\perp}dt=\int v_1dt\) 即 \(\displaystyle \int v_2 \sin \theta dt = \int v_1 dt\) 则 \(\displaystyle \int \sin \theta dt= \frac{v_1t}{v2}\)
所以 \(l=v_2t-\frac{v_1^2}{v_2}t\) ， \(t=\frac{v_2l}{v_2^2-v_1^2}\)