电磁学

电荷，库仑力与电场

起电方式

使物体带电称为起电，起电一般有一下几种方式：
1.摩擦起电
两种物体相互摩擦，可能使其带电
2.接触起电
一个带电的物体与另一个物体接触，可以使其带电
3.感应起电
通过静电感应方式使另一个物体带电

电荷量

描述物体所带电荷的多少的物理量称为电荷量，简称电量，符号 \(Q\) 或 \(q\) ，单位为库伦，简称库，符号 \(C\) 。
通过实验发现，任何物体的电量均为电子电量的整数倍，所以将一个电子的电量称为元电荷，符号为 \(e\) 。
$ e \approx 1.60 \times 10^{-19} C$ 。
电子电量与其质量之比称为电子的比荷。电子的比荷 \(\frac{e}{m_e} \approx 1.76 \times 10^{11} C/kg\)

电荷守恒定律

物体的电荷不会凭空产生，消失。只会在物体间转移。

点电荷

与质点相同，若在计算时，物体的形状对电荷的影响可以忽略不计，我们可以将此物体抽象成一个点，称为点电荷

库仑定律

在真空中两个静止点电荷之间的相互作用力，与两电荷间距离的平方成反比，且与两电荷电量的乘积成正比，作用力方向在它们的连线上，同号电荷相斥，异号电荷相吸。
用矢量形式表示：
\(\displaystyle F=k_e\frac{q_1q_2 \vec{r}}{r^3}\)
若两点电荷电荷符号相同，则 \(q_1q_2>0\) ， \(F\) 与 \(\vec{r}\) 方向相同，表现为斥力。
反之，表现为吸引力。
其中 \(k_e\) 为静电力常量，约为 \(9.0 \times 10^9 N \cdot m^2/C^2\) 。
在大学教材中，\(k\) 通常会写成 \(\frac{1}{4\pi\varepsilon_0}\) 的形式，其中 \(\varepsilon_0=8.85\times 10^{-12} C^2/(N\times m^2)\) 成为真空中的电介常数。
这个力称之为静电力，又称库仑力。
与万有引力公式对比：
\(\displaystyle F=-G\frac{m_1m_2\vec{r}}{r^3}\)
两者有着很大的相似性。

静电场

场是物理学中一种重要的概念。
凡是有电荷的地方就存在电场。
电场会对其中的电荷产生力，称之为电场力。
静置电荷所产生的电场称为静电场。
我们可以向其中放入一个电荷量极小，体积忽略不计的点电荷，此点电荷基本不会堆电场造成影响，来研究电场各处的大小。这个电荷称之为试探电荷。

电场强度

电场强度，是衡量电场能施加力能力的物理量，简称场强，符号 \(E\)，定义为 \(E=\frac{F}q\) ，单位为 \(N/C\)
电场强度(矢量)处处相等的磁场称为匀强磁场。

点电荷的电场强度

由库仑定律，\(\displaystyle E=\frac{F}{q}=\frac{k_e\frac{Qq\vec{r}}{r^3}}{q}=k_e\frac{Q\vec{r}}{r^3}\)
可以看出，点电荷的电场强度与位矢方向相同，与位矢大小的平方成反比，与点电荷电量成正比。

电场线

在电场中每个位置画一条极短曲线，此曲线与该位置电场强度方向相切。

电势能与电势

电场力会对物体做功，我们先来研究匀强磁场电场力做的功。
如下图(图源粤教版必修三P19)

因为在匀强磁场中
\(E,q\) 不变，所以 \(F=Eq\) 不变。
\(\displaystyle W=\int_{t_1}^{t_2} F \cdot d\vec{x}(t) =F \cdot \int_{t_1}^{t_2} d\vec{x}(t) = F \cdot \Delta \vec{x}\)
所以电场力做功只与位移有关。
而与移动路径无关。
教材中也表示，这个结论在非匀强电场中也成立。但是此处的非匀强电场不能随意指定其形态，而是由若干点电荷电场的叠加。
证明略。

电势能

既然电场力做功只与试探电荷的位移有关，那么类似于重力势能，我们定义电势能，符号 \(E_p\) ，单位 \(J\) 。
则 \(W_{AB}=E_{pA}-E_{pB}\) 。
若定义无穷远处的电势能为 \(0\) 。
则一个点的电势能可以这样算：
\(E_{pA}=W_{AO}\)

电势

研究发现，一个试探电荷在电场中其电势能与电量的比值是固定的，定义其为电势，符号 \(\varphi\) ，单位伏特，简称伏，符号 \(V\) ，国际单位制下 \(1V=1J/C\)
由定义： $ \varphi_A = \frac{E_{pA}}{q}$
同电场强度，电势是电场的固有性质，与试探电荷无关。

等势面

电场中电势相等的点构成的集合称为等势面。
显然，等势面有以下性质：

1. 等势面与电场线处处正交。
2. 不同等势面间不相交。
3. 物体沿等势面移动电场力不做功。

下图是常见的等势面与电场线(图源粤教版必修三P22)

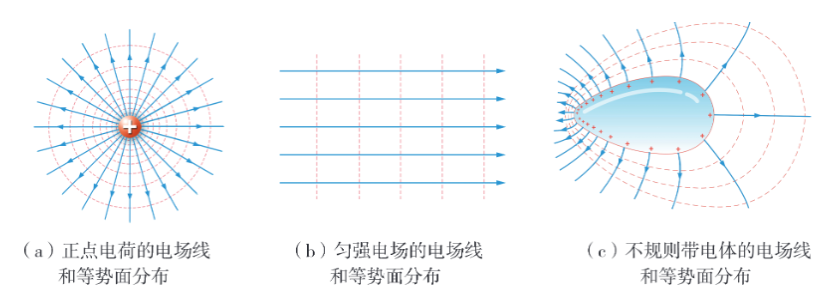
电势差

电场内两点间电势之差称为电势差，亦称电压，符号 \(U\) ， $ U_{AB} = \varphi_A - \varphi_B$
易知： \(U_{AB}=\frac{W_{AB}}{q}\)

电势差与场强

\(U_{AB}=\frac{W_{AB}}{q}=\frac{F \cdot \Delta \vec{x}}{q}=E \cdot \Delta \vec{x} = Ed_{\perp}\)
即电势差等于电场强与位移的点乘积。
\(E=\frac{U}{d_{\perp}}\) 可以看出场强 \(E\) 的另一个单位是 \(V/m\)

拓展

电通量与高斯定理

类比于流量，在静电场中取一个很小的面积元 \(\Delta S\) ，由于 \(\Delta S\) 很小，所以其上面的场强 \(E\) 可视为均匀不变的， 则电通量 \(\Delta \Phi=E \cdot \Delta S\) 。
对于任意封闭曲面 \(S\) 则有 \(\displaystyle\Phi=\iint d\Phi=\iint E \dot dS=4\pi k_e\sum_{S内} q\) (最后一个等号由高斯定理给出)

几种经典带电体的场强

均匀带电球壳

其内部的场强为零
其外部的场强 \(E=k\frac{Q}{r^2}\)
证明略

均匀带电球体

球体外部：
可以把球体看成一个个球壳微元，则 \(E=k\frac{Q}{r^2}=k\frac{4\pi R^3 \rho}{3r^2}\) 。
其中： \(\rho\) 为电荷体积密度。
球体内部：
同上，则 \(E=k\frac{Q}{r^2}=k\frac{4\pi r^3 \rho}{3r^2}=\frac{4}{3}\pi kr\rho\) 。

无限长带电直线

设线电荷密度为 \(\eta\) 则 \(E=k\frac{2\eta}{r}\) 。

无限大带电平面

\(E=2\pi k\sigma\) 其中 \(\sigma\) 为面电荷密度。

电偶极子

两个电荷，等大异号，称为电偶极子。
类似力矩，定义电偶极矩 \(P=ql\)
电偶极矩的电场，对于 \(T\) 点，到电偶极子中点 \(M\) 的距离为 \(r\) ，与电偶极子连线的夹角为 \(\varphi\) 则 \(E_T=k\frac{ql}{r^3}\sqrt{3\cos^2\varphi+1}\) 与 \(TM\) 的夹角 \(\delta\) 有 \(\tan\delta=\frac{1}{2}\tan\varphi\)
电偶极矩的电势，对于 \(T\) 点，同上，则： \(\varphi_+=\frac{kq}{r_+},\varphi_-=\frac{k(-q)}{r_-}\) 相加化简得： \(\varphi_T=\frac{ql\cos\theta}{r^2}=\frac{P\cos\theta}{r^2}\)

电容

处于静电平衡的绝缘导体是个等势体，导体的电势是由导体所带电荷量与导体本身得大小和形状决定的。
通常把孤立导体所带电荷量与导体电势的比值成为导体的电容，即 \(C=\frac{Q}{\varphi}\) 。
平行板电容器：
\(\displaystyle C=\frac{Q}{\varphi}=\frac{Q}{Ed}=\frac{\sigma S}{4\pi k \sigma d}=\frac{S}{4\pi k d}\) 。
同轴圆柱形电容器：
高为 \(H\) 半径分别为 \(R_1,R_2\) 的两个圆筒同轴嵌套放置，其间充以电介常数为 \(\varepsilon\) 的电介质。
\(H \gg R_2\) 且 \(R_2 \gg d=R_2-R_1\)
\(C=\frac{\varepsilon RH}{2kd}\)
同心球型电容器:
\(\displaystyle \varphi=\varphi_内-\varphi_外=k\frac{Q}{\varepsilon R_1}-k\frac{Q}{\varepsilon R_2}=k\frac{Q}{\varepsilon}(\frac{1}{R_1}-\frac{1}{R_2})\)
\(\displaystyle C=\frac{Q}{\varphi}=\frac{\varepsilon R_1R_2}{k(R_2-R_1)}\)

电场/带电物体的能量

带电物体的能量

我们可以假设刚开始物体不带电，所有电荷均分布在无穷远处，将这些电荷一道带电物体上，所需克服电场力做的功即为带电物体的能量。
设其电容为 \(C\)
\(W=\int_0^Q dE\)
分析电势：
\(\varphi=\frac{Q}{C}\) ，则 \(\varphi\) 是关于 \(Q\) 的一次函数
又 \(\varphi=\frac{E}{Q}\)
则 \(E=Q\varphi\)
\(\displaystyle W=\int_0^Q dE=\int\varphi dQ=\int\frac{Q}{C}dQ=\frac{Q^2}{2C}=\frac{1}{2}Q\varphi=\frac{1}{2}C\varphi^2\)

电场的能量

以下只讨论平行板电容器的电场能量，其余则大同小异，我也不会证。
\(\displaystyle E=\frac{1}{2}CU^2=\frac{1}{2} \cdot\frac{S}{4\pi k d}\cdot (Ed)^2=\frac{E^2Sd}{8\pi k}\)
可以发现，此能量不仅与 \(E^2\) 成正比，还与 \(Sd=V\) 成正比。
定义电场能量密度 \(\displaystyle \omega=\frac{E^2}{8\pi k}\)
对任意电场均有效。

电场中的导体与静电平衡

处于电场中的导体，由于外电场力的作用，导体的两端会出现等量异种电荷。
此现象称为静电感应。
产生的电荷称为感应电荷。
感应电荷的电场贺外电场叠加，会导致导体内部电场为 \(0\) 。
内部电子停止定向移动，这种状态称之为静电平衡。
处于静电平衡状态下的导体有以下性质：

1. 导体内部场强为 \(0\) 。
2. 导体表面是等势面，整个导体是等势体
3. 净电荷只分布在导体外表面上(运用1.与高斯定理)
4. 导体表面处场强的方向一定与导体表面正交

恒稳电流

部分电路欧姆定律

电流

电荷的定向移动形成电流，形成电流的条件是：存在自由电荷，导体两端有电势差(存在电场)
电流强度：$ I=\frac{dQ}{dt}=neSv $

电阻

导体的电阻由其本身性质与温度决定
$ R=\rho \frac{L}{S} $
温度变化不大时 $ \rho_t=\rho_0(1+at) $

欧姆定律

\(I=\frac{U}{R}\)

电功

电流在电路中做的功叫做电功，其实际上是电场做的功
\(W=qU=It\cdot U=IUt\)
导体中通过电流时会有热量放出，英国科学家焦耳通过实验得出
\(Q=I^2Rt\)

电阻的计算

1. 等电势节点断、接
2. 电流分布法，假设有电流 \(I\) 从 \(A\) 流入，从 \(B\) 流出，又两点间电压一定，与电流路线无关，通过 \(R=\frac{U}{I}\) 解决
3. 无穷网络等效替代，先设出 \(R_k\) 再推导出 \(R_k+1\) 。最后令 \(k\rightarrow+\infty\) 即可。
4. \(Y-\triangle\)变换法： \(R_{12}=\frac{R_1R_2+R_2R_3+R_3R_1}{R_3}\) ， \(R_1=\frac{R_{12}R_{31}}{R_{12}+R_{23}+R_{31}}\) 。

基尔霍夫定律

动电势

电源搬运单位正电荷经电源内部从负极到正极所做的功称为电源电动势，用 \(E\) 表示。
若顺接，其相当于一个电阻，其 \(IR=E\) 。

闭合电路欧姆定律

\(\displaystyle I=\frac{\sum E}{\sum R}\)

基尔霍夫定律

I. \(\displaystyle \sum I_入=\sum I_出\)
II. \(\displaystyle \sum E+\sum IR=0\)

含容电路

电容器无电流通过。

空位待补

磁场

磁场对电流的作用

磁感应强度

磁感应强度为矢量，与该点磁针N极所指方向相同。
\(\displaystyle B=\frac{F}{IL}\)

磁感线

同电场线，磁感线与磁感应强度处处相切。

毕奥-萨伐而定律：

\(\displaystyle d\vec{B}=\frac{\mu_0}{4\pi}\frac{Id\vec{l}\times\vec{r}}{r^3}\)
无限长导线：
\(B=\frac{\mu_0I}{2\pi r_0}\)
圆形导线轴线上：
\(r=0\) 时 \(\displaystyle B=\frac{\mu_0I}{2R}\)
\(r\gg R\) 时 \(\displaystyle B=\frac{\mu_0R^2I}{2r^3_0}\)

安培环路定律

\(\displaystyle \oint_L B\cdot dl=\mu_0\sum_{L内}I\)

安培力

\(d\vec{F}=Id\vec{L}\times\vec{B}\)

磁场对载流线圈的作用

力偶矩 \(\vec{M}=\vec{m}\times \vec{B}\)
其中磁矩 \(m=NIS\) 为右旋法矢量。
\(e_m=e_{I1}\times e_{I2}\) ， \(N\) 为匝数， \(S\) 为线圈面积。

磁场对运动电荷的作用

洛伦兹力

\(F=q\vec{v}\times\vec{B}\)
显然，\(F\perp\vec{v}\)
所以洛伦兹力不做功。

带电粒子在磁场中的运动

匀强磁场中：
若 \(v // B\) 则带电粒子做匀直运动
若 $ \perp B$ 则带电粒子做匀速圆周运动
\(\displaystyle R=\frac{mv^2}{F}=\frac{mv^2}{qvB}=\frac{mv}{qB}\)
\(\displaystyle T=\frac{2\pi R}{v}=\frac{2\pi m}{qB}\)
若呈 \(\theta\) 角
则轨迹为等距螺旋线
\(\displaystyle R=\frac{mv_{\perp}}{qB}=\frac{mv\sin\theta}{qB}\)
$\displaystyle h=v_{//}T=v\cos\theta\frac{2\pi m}{qB}=\frac{2\pi m\cos\theta}{qB} $

公式汇总

\(\displaystyle F=k\frac{Qq}{r^2}\)
\(\displaystyle E=\frac{F}{q}=k\frac{Q}{r^2}\)
\(\displaystyle W_e=\int F\cdot d\vec{x}\)
\(\displaystyle W_e=F\cdot \Delta \vec{x}\) ，匀强电场
\(\displaystyle W_{AB}=E_{pA}-E_{pB}\)
\(\displaystyle E_{pA}=W_{AO}\) ，\(O\) 为无穷远点
\(\displaystyle \varphi_A=\frac{E_{pA}}{q}=\frac{\int_{A}^{O}F \cdot d\vec{x}}{q}=\int_{A}^{O}E \cdot d\vec{x}\)
\(U_{AB}=\varphi_A-\varphi_B\)
\(\displaystyle U_{AB}=\frac{W_{AB}}{q}\)
\(\displaystyle \Phi=\iint d\Phi=\iint E \cdot dS= 4 \pi k \sum_{S内} q\)