浮点数的存储、转换和运算

参考 wdliming
整数和小数相对
定点存储格式和浮点存储格式相对 定点浮点指存储格式
C语言使用定点存储格式存储整数，使用浮点存储格式存储小数。
数值范围和数值精度是选择存储格式时需要重点考虑和权衡的指标。
数值范围小，则能表达的有效数字范围受限制，可能无法满足实际应用的需要。
数值精度不够，可能导致运算时丢失的精度较多误差较大。
浮点数可以在计算机中近似表示任意实数。注意是近似表示。
浮点数的存储，以float为例，占用4字节
符号 指数 尾数
bit31 b30-b23 b22-b0
浮点数转换到内存中存储分为3步。以21.625为例，转为float

1. 转为二进制
   整数部分除2取余，21--10101
   小数部分乘2取整 0.625--101
   即10101.101
2. 用科学技术法表示
   10101.101---1.0101101*2exp4
3. 计算指数
   4--offset 127 = 131 10000011 why offset 127 --个人的理解就是将指数部分变成了无符号数，即0-255范围，减去127即-127 - +128的指数范围
   最后，float存储如下
   符号 指数 尾数 --科学技术法表示的小数点部分
   bit31 b30-b23 b22-b0
   0 10000011 0101101 00000000 00000000

double占用8个字节。存储如下 ==ofset 1023 4+1023=1027 --省了一个符号位，-1023 - +1024
符号 指数 尾数
bit63 b62-b52 b51-b0
1 100 00000011 01011010 00000000 00000000 ....

数值范围
指数部分的最大值决定了数值范围。
float,仅考虑指数部分，2exp128=3.40E+38，则范围为-3.40E+38 - +3.40E+38。 整数部分为1，小数部分为1-2exp(-23),加起来为2-2exp(-23).
double,仅考虑指数部分，2exp1024=1.8E+308，则范围为-1.8E+308 ~ +1.8E+308。 整数部分为1，小数部分为1-2exp(-52),加起来为2-2exp(-52).

精度
float和double的精度是由尾数的位数来决定的，尾数越多能表示的小数点后面有效数字就越多，因此精度就越高。浮点数在内存中是按科学计数法来存储的，其整数部分始终是一个隐含着的“1”，由于它是不变的，故不能对精度造成影响。
float：2^23 = 8388608，一共七位，这意味着最多能有 7 位有效数字，但绝对能保证的为 6 位，也即float的精度为 6~7 位有效数字；
double：2^52 = 4503599627370496，一共 16 位，同理，double的精度为 15~16 位。
所以float叫单精度，double叫双精度

通用处理器中如何进行浮点运算
X86中的XMM寄存器有128bit，可以用来支持浮点运算。
也会有专门的汇编指令，比如movss,移动单精度浮点数。
比如下面的*2

单精度向双精度的转换指令

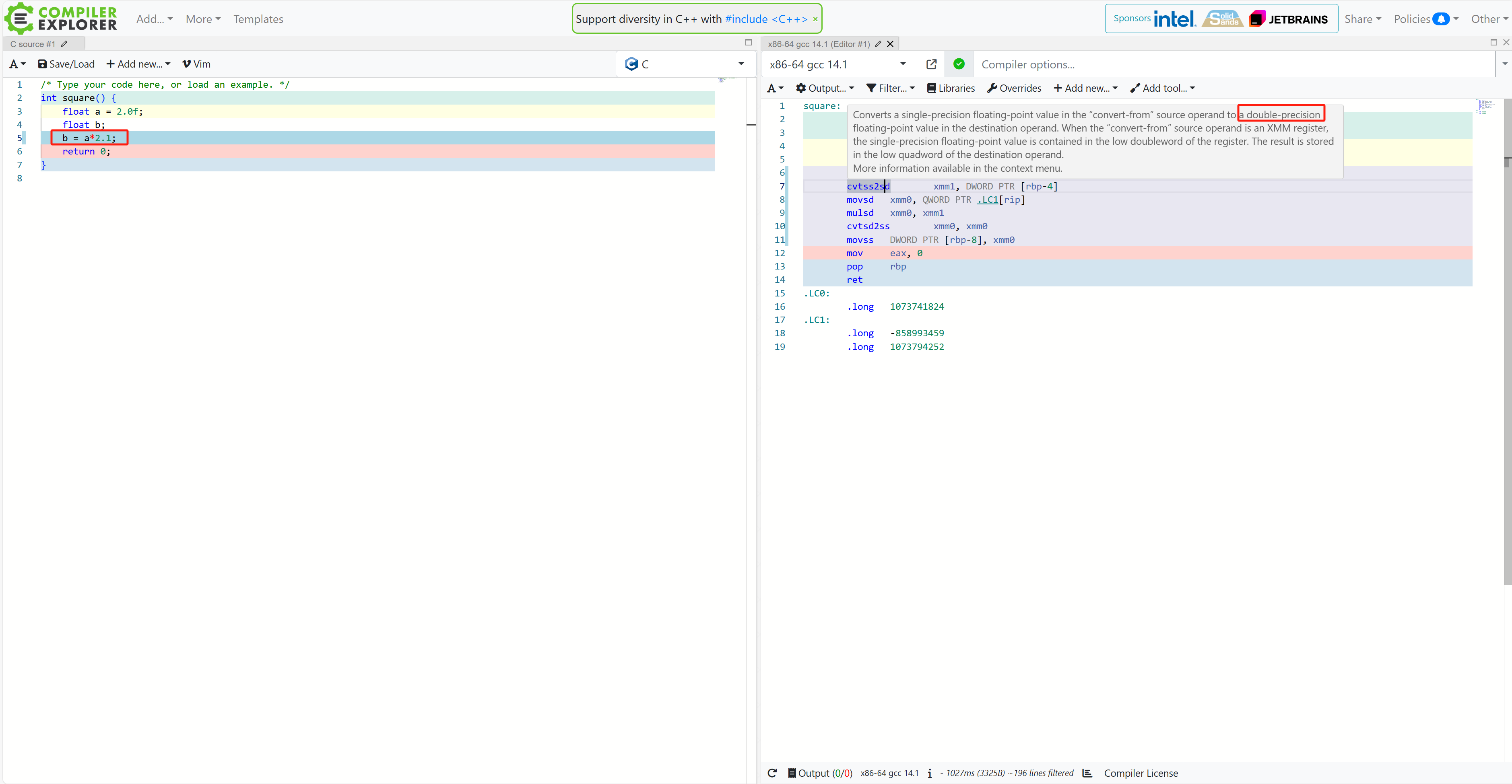
那个mulsd就是浮点乘的指令

问题：2.0f, 2.1f是怎么变成上面图中存储好的浮点数的？ 应该是编译器做的