树状数组
树状数组
一、用处
有时候题目会要求维护一个数组的前缀和，朴素调整的话最坏是O（n）的复杂度
而当我们学会了 “树状数组” ，他的修改与求和都是O（logn）的
常见用于：
（1）单点修改，区间查询
（2）区间修改，单点查询（差分实现）
二、基本思想
任意一个正整数都可以被 “二进制分解”
比如区间 [1,n] 可以分解成 logx个小区间
树状数组就是就是基于以上操作的一种数据结构，基本用途是维护前缀和。对于区间[1, x ] ，树状数组将他分解为logx个子区间，从而满足快速询问区间和。
三、基本算法
子区间的共同特点是：若区间结尾为R，则区间长度就等于R的“二进制分解”下的最小二次幂，设为lowbit(R)
对于给定的序列A，建立一个数组c，c[x]保存序列A的区间 [ x-lowbit(x)+1，x ] 中所有数字的和
你看下面这个图：
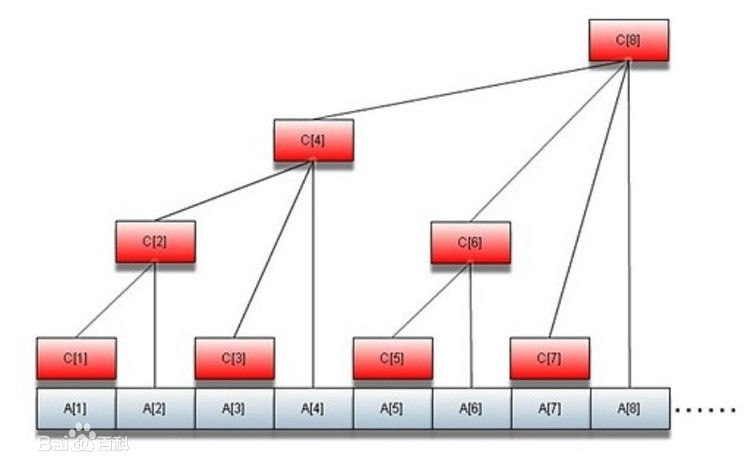
该结构满足以下性质：
（1）每个内部节点c[x]保存以他为根的子树中所有叶节点的和
（2）每个内部节点c[x]的子节点数等于lowbit(x)的大小
（3）除数根外，每个内部节点c[x]的父节点是c[x+lowbit(x)]
（4）树的深度为O(logN)
1.求lowbit（x）
int lowbit(int x) { return x&-x; }
2.单点修改
当我们修改了单点的值，与它相关的父节点的值也会相应的发生改变，上传维护，由子及父
void updata(int x,int v) { while(x<=n) { c[x]+=v; x+=lowbit(x); } }
3.查询前缀和
由父及子
int sum(int x) { int ans=0; while(x>0) { ans+=c[x]; x-=lowbit(x); } return ans; }
4.区间求和
Σx~y = sum(y) - sum(x-1)
5.扩展（多维树状数组）
如果有n*m的二维数组a，树状数组为c，那么单点修改和求前缀和就有以下操作：
int updata(int x,int y,int z) { int i=x; while(i<=n) { int j=y; while(j<=m) { c[i][j]+=z; j+=lowbit(j); } i+=lowbit(i); } }
int sum(int x,int y) { int ans=0,i=x; while(i>0) { int j=y; while(j>0) { ans+=c[i][j]; j-=lowbit(j); } i-=lowbit(i); } return ans; }
6.注意事项
树状数组能处理的是下标为1~n的数组，下标绝对不能为0，lowbit（0）=0，这样会陷入死循环
四、典型例题
（1）单点修改，区间查询
P3374 【模板】树状数组 1
非常正宗的板子题了
#include<bits/stdc++.h> using namespace std; const int maxn=5e5+10; int n,m,opr,x,y,k; int c[maxn]; inline int read() { int ans=0; char last=' ',ch=getchar(); while(ch<'0'||ch>'9') last=ch,ch=getchar(); while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } int lowbit(int x) { return x&-x; } void updata(int x,int v) { while(x<=n) { c[x]+=v; x+=lowbit(x); } } int sum(int x) { int ans=0; while(x>0) { ans+=c[x]; x-=lowbit(x); } return ans; } int main() { n=read();m=read(); for(int i=1;i<=n;i++) { k=read(); updata(i,k); } for(int i=1;i<=m;i++) { opr=read();x=read();y=read(); if(opr==1) updata(x,y); if(opr==2) printf("%d\n",sum(y)-sum(x-1)); } return 0; }
（2）区间修改，单点查询
P3368 【模板】树状数组 2
题解
这里是用差分来实现
什么是差分？？
给出一个数列 A1 A2 A3 A4 A5 。。。。An
用数组 c[ i ] 来记录A i 与 A i-1的差，即 c[ i ] = A[ i ] - A[ i-1 ]
那么当我们想要修改区间 [ x,y ]的值的时候，区间里每个数都加上相同的数字，c[i+1]~c[j]都是不变的，改变的只是 c[ i ] 和 c[ j+1 ] ，由于是区间加，c[ i ] 自然就变大了，c[ j+1 ] 自然就变小了
这时用二维数组维护差分数组就行了，每次区间修改只需要改两个值
单点查询呢？ A x = Σ c[ i ] (i=1~i)
#include<bits/stdc++.h> using namespace std; const int maxn=5e5+10; int n,m,opr,x,y,k; int c[maxn],a[maxn]; inline int read() { int ans=0; char last=' ',ch=getchar(); while(ch<'0'||ch>'9') last=ch,ch=getchar(); while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar(); if(last=='-') ans=-ans; return ans; } int lowbit(int x) { return x&-x; } void updata(int x,int v) { while(x<=n) { c[x]+=v; x+=lowbit(x); } } int sum(int x) { int ans=0; while(x>0) { ans+=c[x]; x-=lowbit(x); } return ans; } int main() { n=read();m=read(); for(int i=1;i<=n;i++) { a[i]=read(); updata(i,a[i]-a[i-1]); } for(int i=1;i<=m;i++) { opr=read(); if(opr==1) { x=read();y=read();k=read(); updata(x,k); updata(y+1,-k); } if(opr==2) { x=read(); printf("%d\n",sum(x)); } } return 0; }
五、后记
能用树状数组做的题，线段树也能做；
但能用线段树做的，树状数组不一定能做。
它比线段树优秀是什么情况呢？？
- 线段树常数过大时
- 线段树功能过多时
树状数组可求的所有问题必须存在逆元
