Batch Normalization

• 从 Mini-Batch SGD 说起

我们先从 Mini-Batch SGD 的优化过程讲起，因为这是下一步理解 Batch Normalization 中 Batch 所代表具体含义的知识基础。

我们知道，SGD 是无论学术圈写文章做实验还是工业界调参跑模型最常用的模型优化算法，但是有时候容易被忽略的一点是：一般提到的 SGD 是指的 Mini-batch SGD，而非原教旨意义下的单实例 SGD。

                                               

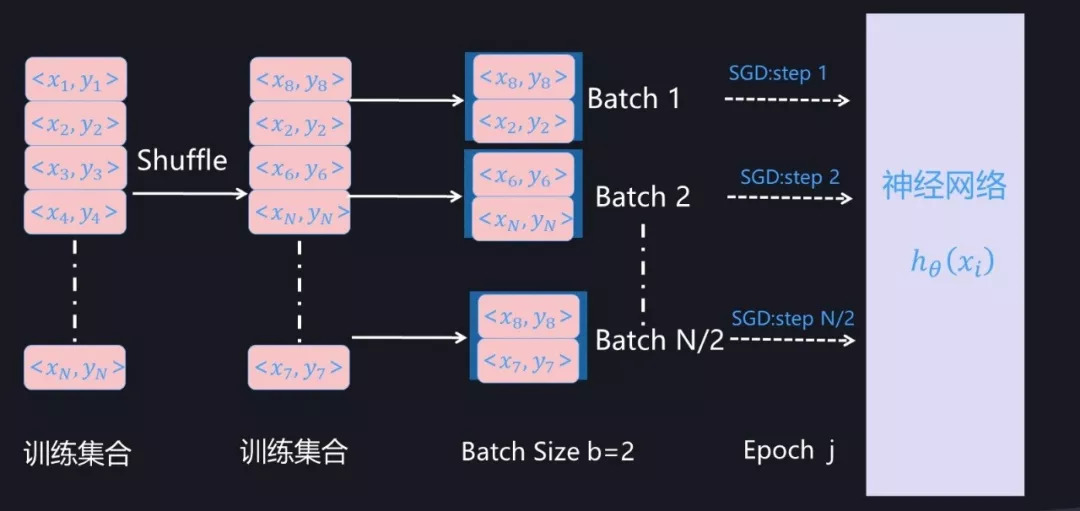
                                                             图 1. Mini-Batch SGD 训练过程（假设 Batch Size=2）

所谓「Mini-Batch」, 是指的从训练数据全集 T 中随机选择的一个训练数据子集合。假设训练数据集合 T 包含 N 个样本，而每个 Mini-Batch 的 Batch Size 为 b，于是整个训练数据可被分成 N/b 个 Mini-Batch。在模型通过 SGD 进行训练时，一般跑完一个 Mini-Batch 的实例，叫做完成训练的一步（step）, 跑完 N/b 步则整个训练数据完成一轮训练，则称为完成一个 Epoch。完成一个 Epoch 训练过程后，对训练数据做随机 Shuffle 打乱训练数据顺序，重复上述步骤，然后开始下一个 Epoch 的训练，对模型完整充分的训练由多轮 Epoch 构成（参考图 1）。

在拿到一个 Mini-Batch 进行参数更新时，首先根据当前 Mini-Batch 内的 b 个训练实例以及参数对应的损失函数的偏导数来进行计算，以获得参数更新的梯度方向，然后根据 SGD 算法进行参数更新，以此来达到本步（Step）更新模型参数并逐步寻优的过程。

                  

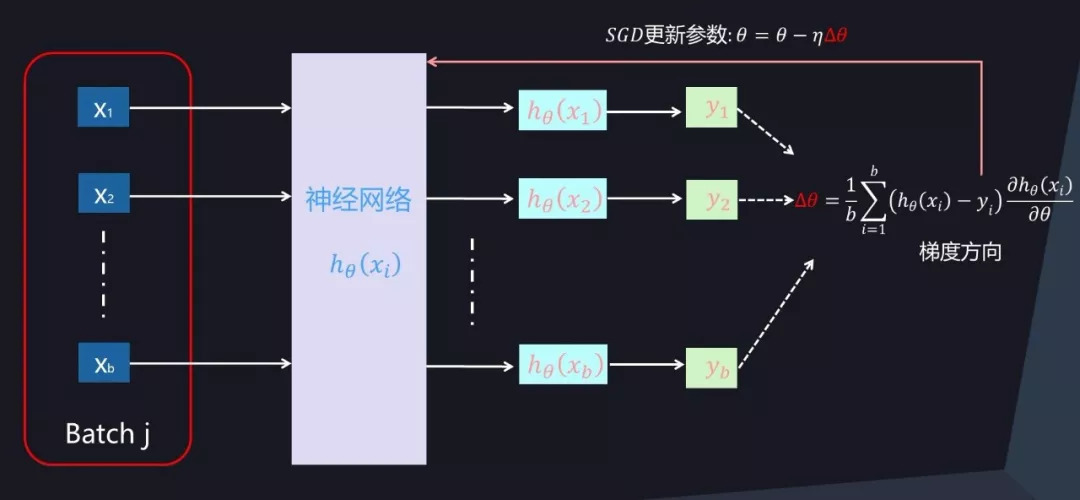
                                               图 2. Mini-Batch SGD 优化过程

具体而言，如果我们假设机器学习任务的损失函数是平方损失函数：

                                             

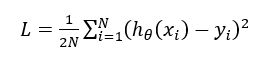
那么，由 Mini-Batch 内训练实例可得出 SGD 优化所需的梯度方向为：

                                             

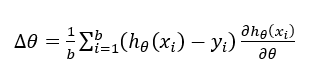
其中，<x_i,y_i>是 Mini-Batch 内第 i 个训练实例对应的输入 x_i 和值 y_i。h_θ是希望学习到的映射函数，其中θ是函数对应的当前参数值。代表了 Mini-Batch 中实例 i 决定的梯度方向，Batch 内所有训练实例共同决定了本次参数更新的梯度方向。

根据梯度方向即可利用标准 SGD 来更新模型参数：

                                                               

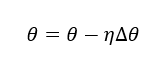
其中，η是学习率。

• Normalization到底在做什么

对于神经元的激活值来说，不论哪种 Normalization 方法，其规范化目标都是一样的，就是将其激活值规整为均值为 0，方差为 1 的正态分布。即规范化函数统一都是如下形式：

                                          

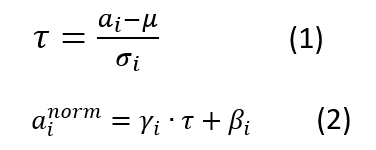
写成两步的模式是为了方便讲解，如果写成一体的形式，则是如下形式：

                                    

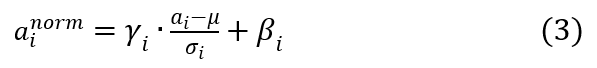
其中，a_i 为某个神经元原始激活值，为经过规范化操作后的规范后值。整个规范化过程可以分解为两步，第一步参考公式（1），是对激活值规整到均值为 0，方差为 1 的正态分布范围内。其中，μ 是通过神经元集合 S（至于 S 如何选取读者可以先不用关注，后文有述）中包含的 m 个神经元各自的激活值求出的均值，即：

                                    

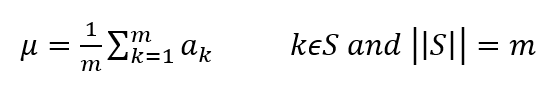
σ_i 为根据均值和集合 S 中神经元各自激活值求出的激活值标准差：

                               

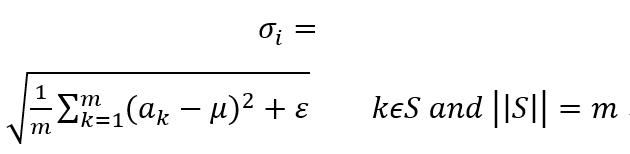
其中，ε 是为了增加训练稳定性而加入的小的常量数据。

第二步参考公式（2），主要目标是让每个神经元在训练过程中学习到对应的两个调节因子，对规范到 0 均值，1 方差的值进行微调。因为经过第一步操作后，Normalization 有可能降低神经网络的非线性表达能力，所以会以此方式来补偿 Normalization 操作后神经网络的表达能力。

• BN怎么做

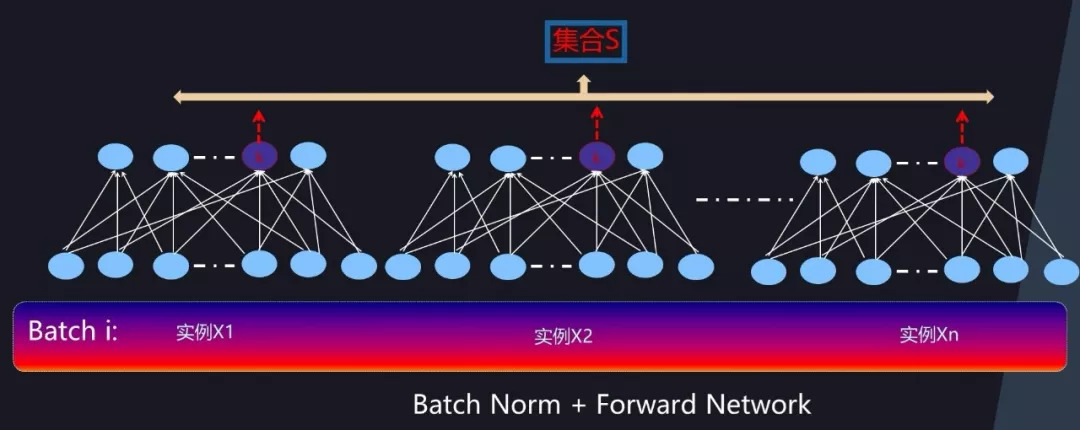
对于前向神经网络来说，BatchNorm 在计算隐层某个神经元 k 激活的规范值的时候，对应的神经元集合 S 范围是如何划定呢？图 6 给出了示意。因为对于 Mini-Batch 训练方法来说，根据 Loss 更新梯度使用 Batch 中所有实例来做，所以对于神经元 k 来说，假设某个 Batch 包含 n 个训练实例，那么每个训练实例在神经元 k 都会产生一个激活值，也就是说 Batch 中 n 个训练实例分别通过同一个神经元 k 的时候产生了 n 个激活值，BatchNorm 的集合 S 选择入围的神经元就是这 n 个同一个神经元被 Batch 不同训练实例激发的激活值。划定集合 S 的范围后，Normalization 的具体计算过程与前文所述计算过程一样，采用公式 3 即可完成规范化操作。

3.2 CNN 网络中的 BN
了解了前向神经网络中的 BatchNorm，接下来介绍 CNN 中的 BatchNorm，读者可以先自行思考下如果由你来主导设计，在 CNN 中究竟应该如何确定神经元集合 S 的势力范围。

我们知道，常规的 CNN 一般由卷积层、下采样层及全连接层构成。全连接层形式上与前向神经网络是一样的，所以可以采取前向神经网络中的 BatchNorm 方式，而下采样层本身不带参数所以可以忽略，所以 CNN 中主要关注卷积层如何计算 BatchNorm。

CNN 中的某个卷积层由 m 个卷积核构成，每个卷积核对三维的输入（通道数*长*宽）进行计算，激活及输出值是个二维平面（长*宽），对应一个输出通道（参考图 7），由于存在 m 个卷积核，所以输出仍然是三维的，由 m 个通道及每个通道的二维平面构成。

                           

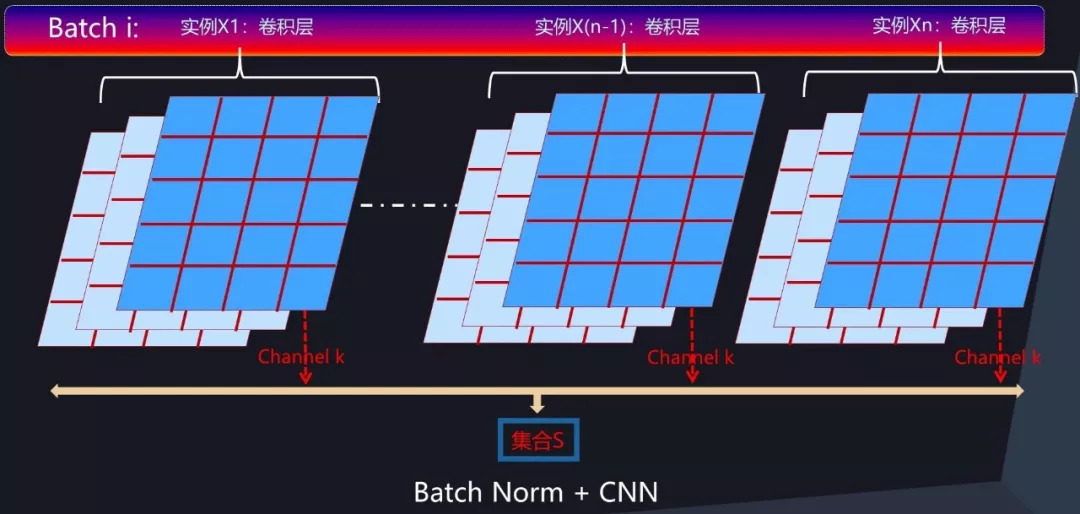
                                                             图 8. CNN 中的 BatchNorm 过程

那么在卷积层中，如果要对通道激活二维平面中某个激活值进行 Normalization 操作，怎么确定集合 S 的范围呢？图 8 给出了示意图。类似于前向神经网络中的 BatchNorm 计算过程，对于 Mini-Batch 训练方法来说，反向传播更新梯度使用 Batch 中所有实例的梯度方向来进行，所以对于 CNN 某个卷积层对应的输出通道 k 来说，假设某个 Batch 包含 n 个训练实例，那么每个训练实例在这个通道 k 都会产生一个二维激活平面，也就是说 Batch 中 n 个训练实例分别通过同一个卷积核的输出通道 k 的时候产生了 n 个激活平面。假设激活平面长为 5，宽为 4，则激活平面包含 20 个激活值，n 个不同实例的激活平面共包含 20*n 个激活值。那么 BatchNorm 的集合 S 的范围就是由这 20*n 个同一个通道被 Batch 不同训练实例激发的激活平面中包含的所有激活值构成（对应图 8 中所有标为蓝色的激活值）。划定集合 S 的范围后，激活平面中任意一个激活值都需进行 Normalization 操作，其 Normalization 的具体计算过程与前文所述计算过程一样，采用公式 3 即可完成规范化操作。这样即完成 CNN 卷积层的 BatchNorm 转换过程。

————————————————
版权声明：本文为CSDN博主「展希希鸿」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_28266311/article/details/90759132