算法题（二）

1、罗马数字转整数

 

 

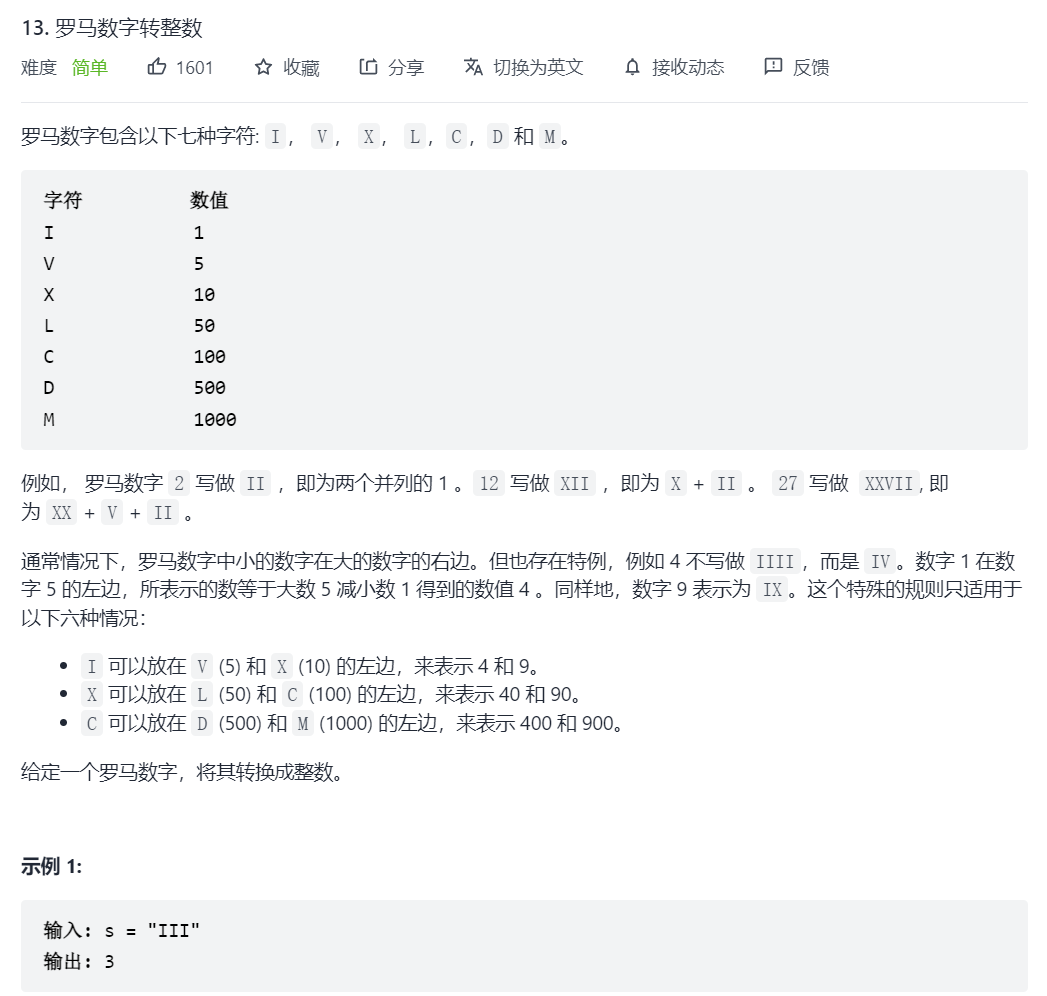
解题思路：罗马数字转整数只有两种情况，一种是正常情况，即右边的数字比左边的小，这种是做加法；另外一种是右边数字比左边数字大，这种情况要做减法。因此可以多往后看一位以确定究竟是做加法还是做减法。时间复杂度O(n)，空间复杂度O(1)。

class Solution(object):
    def romanToInt(self, s):
        """
        :type s: str
        :rtype: int
        """
        # 正常：左大有小
        # 异常：左小右大
        dict_a = {"I":1,"V":5,"X":10,"L":50,"C":100,"D":500,"M":1000}
        length = len(s)
        i = 0
        res = 0
        while i < length:
            if (i+1) < length:
                if dict_a[s[i+1]]>dict_a[s[i]]:
                    temp = dict_a[s[i+1]] - dict_a[s[i]]
                    res += temp
                    i+=2
                else:
                    res += dict_a[s[i]]
                    i+=1
            else:
                res += dict_a[s[i]]
                break
        return res

 

2、最长公共前缀

 

 

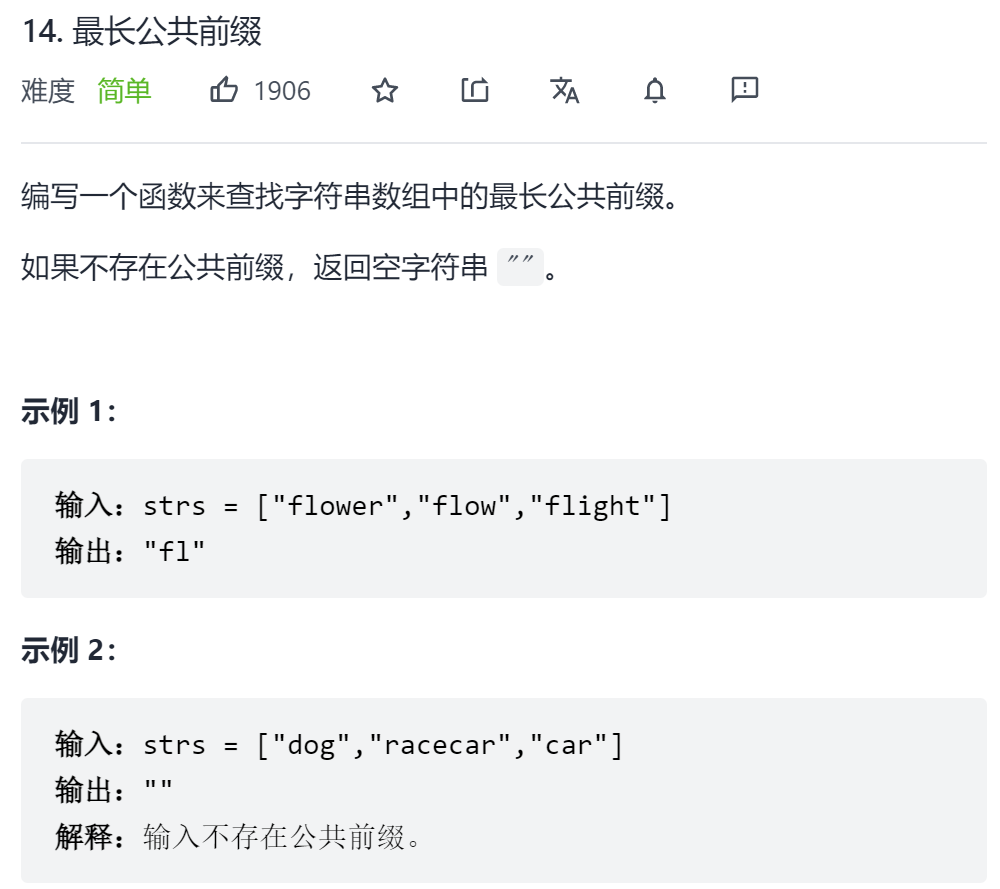
解题思路：遍历数组，两两比较，将结果保存到中间值中。时间复杂度O(n)，空间复杂度O(1)。

class Solution(object):
    def longestCommonPrefix(self, strs):
        """
        :type strs: List[str]
        :rtype: str
        """
        commom_pre = strs[0]
        for i in range(len(strs)):
            if i+1 < len(strs):
                temp = ''
                for j in range(min(len(commom_pre),len(strs[i+1]))):
                    if commom_pre[j] == strs[i+1][j]:
                        temp+=commom_pre[j]
                    else:
                        break
                if len(temp) ==0:
                    return ""
                else:
                    commom_pre = temp
            else:
                break
        return commom_pre

 

3、有效括号

 

 

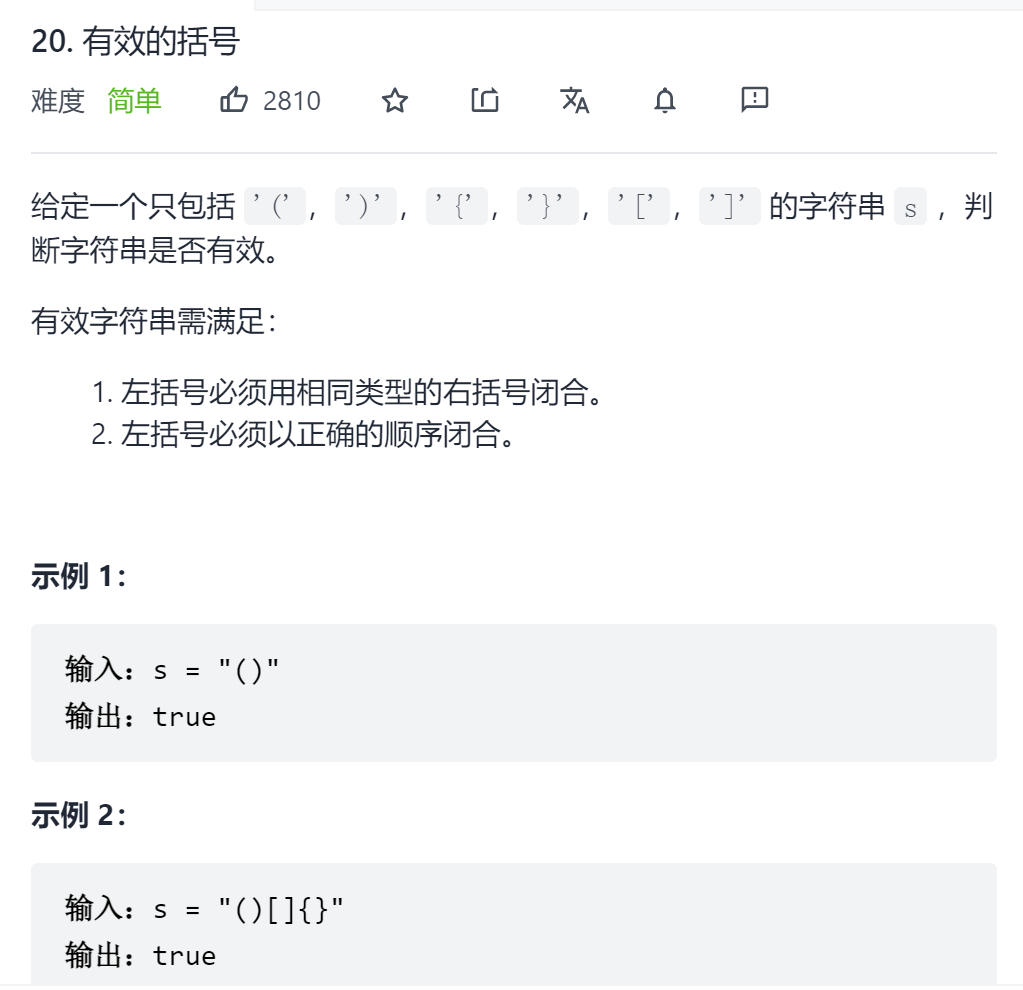
解题思路：如果从字符串指针遍历的角度来分析，这道题就异常复杂。如果使用类似“消消乐”的方式来看待，则会发现一个规律，即我们对于括号的判断是由内而外，即只要内部满足，则不再关注其他逻辑，那是不是意味着可以将满足条件的括号都消除掉呢？由此引入栈每次由内而外取元素进行判断，即只要满足条件则将括号弹出，栈内只保留待判断的括号。时间复杂度O（n），空间复杂度O（n）。

class Solution(object):
    def isValid(self, s):
        """
        :type s: str
        :rtype: bool
        """
        if len(s)%2 ==1:
            return False
        hash_map = {
                    ")":"(",
                    "]":"[",
                    "}":"{"}
        stack = []
        for i in s:
            if i in hash_map:       #即右括号，就进行判断
                #栈不为空，或括号不匹配，则返回false
                if not stack or stack[-1] != hash_map[i]:  
                    return False
                stack.pop()
            else:
                stack.append(i)     #即左括号，就入栈
        return not stack