堆和堆排序

堆的定义：

1. 堆是一棵完全二叉树。

2. 大根堆：

  堆的每一个子树的父亲永远大于其左孩子和右孩子，如下图：

  

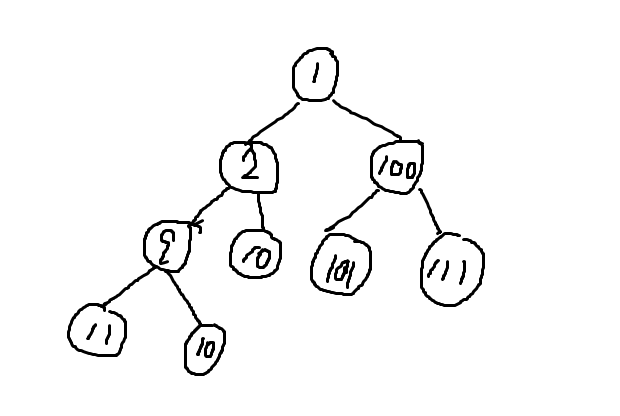
3.小根堆：

  堆的每一个子树的父亲永远小于于其左孩子和右孩子。

堆的性质：

1. 小根堆的堆顶永远存放着最小值，大根堆的堆顶永远存放着最大值

2. 堆的每一层上的数不一定比下一层全部要小或大。

3. 因为是一颗完全二叉树，所以用数组存储即可，父节点下标为i，则left_child=i*2, right_child=i*2+1.

 

堆的操作：

建立一个小根堆：

在堆尾加入元素（当前结点）并比较它与父节点的大小，若大于则结束，否则交换他们的值并把父节点置为当前节点，向上调整。

代码：

int heap[100000000];
void put(int x){
	int pa,son;
	heap[++heap_size]=x;
	son=heap_size;
	while(son>1){
		pa=(son/2);
		if(heap[pa]<=heap[son]) break;
		swap(heap[pa],heap[son]);
		son=pa;
	}
}

建立一个大根堆：

只需要改动一个地方(第8 行)：

if(heap[pa]<=heap[son]) break;

改为：

if(heap[pa]>=heap[son]) break; 

 

取出一个（堆顶）元素（这里以小根堆为例）：

1.取出堆顶值。

2.把堆的最后一个元素放到堆顶上，并把堆的长度减一。

3.从上到下动态调整，每一次取左右子节点中较大的进行交换，并将当前指针指向下一个（被交换的）位置。

代码如下：

int get(){//获得堆顶元素
	int now,next;
	int res;
	res=heap[1];//获取堆顶元素
	heap[1]=heap[heap_size--];//将堆底最后一个元素放到堆顶；
	now=1;
	while(now*2<=heap_size){//保证now不在最后一层（否则next会超出范围）
		next=now*2;//先选左节点
		if(next<heap_size&&heap[next+1]<heap[next]) next++;//判断是选择左结点还是右结点，若执行了则选了右结点（别忘了在保证不超堆的范围内）
		if(heap[now]<=heap[next]) return res;//如果放上去的无需调整则直接结束
		swap(heap[now],heap[next]);
		now=next; 
	}
	return res;
}

 

堆排序：

输入n个数，将n个数从小到大输出：

解析：

  建立一个小根堆，然后每次取出堆顶即可，这就是堆排序。

代码1：

#include<iostream>
using namespace std;
int heap[100000000];

int heap_size=0;
//建堆(小根堆)
void put(int x){
	int pa,son;
	heap[++heap_size]=x;
	son=heap_size;
	while(son>1){
		pa=(son/2);
		if(heap[pa]<=heap[son]) break;
		swap(heap[pa],heap[son]);
		son=pa;
	}
}

int get(){//通过获得堆顶元素（最小值）来实现从小到大排序
	int now,next;
	int res;
	res=heap[1];//获取堆顶元素
	heap[1]=heap[heap_size--];//将堆底最后一个元素放到堆顶；
	now=1;
	while(now*2<=heap_size){//保证now不在最后一层（否则next会超出范围）
		next=now*2;//先选左节点
		if(next<heap_size&&heap[next+1]<heap[next]) next++;//判断是选择左结点还是右结点
		if(heap[now]<=heap[next]) return res;
		swap(heap[now],heap[next]);
		now=next; 
	}
	return res;
}

int main(){
	int n,x;
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>x;
		put(x);
	}
	for(int i=1;i<=n;i++){
		cout<<get()<<' ';
	}
	cout<<endl;
	return 0;
}

小结：

堆排序效率较高，时间复杂度为：O(nlog2n)，是一种不稳定的排序方法。

优先队列：

有关优先队列的相关介绍请参考：https://www.cnblogs.com/xiaotan-js/p/16644818.html

一般来说，没人会手写堆和堆排序，以上就是关于堆这一数据结构的介绍，而真正使用堆，大部分人都会选择STL中的优先队列：

代码2：

#include<queue>
#include<iostream>
using namespace std;
priority_queue<int,vector<int>,greater<int> > q;
int n,x;
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>x;
		q.push(x);
	}
	for(int i=1;i<=n;i++){
		cout<<q.top()<<' ';
		q.pop();
	}
	return 0;
}

是不是简洁很多？