算法day13——二叉树（3）

目录

1. 完全二叉树的节点个数
2. 平衡二叉树110
3. 二叉树的所有路径257
4. 左叶子之和404

一、完全二叉树的节点个数

 https://leetcode.cn/problems/count-complete-tree-nodes/description/?envType=problem-list-v2&envId=8At1GmaZ

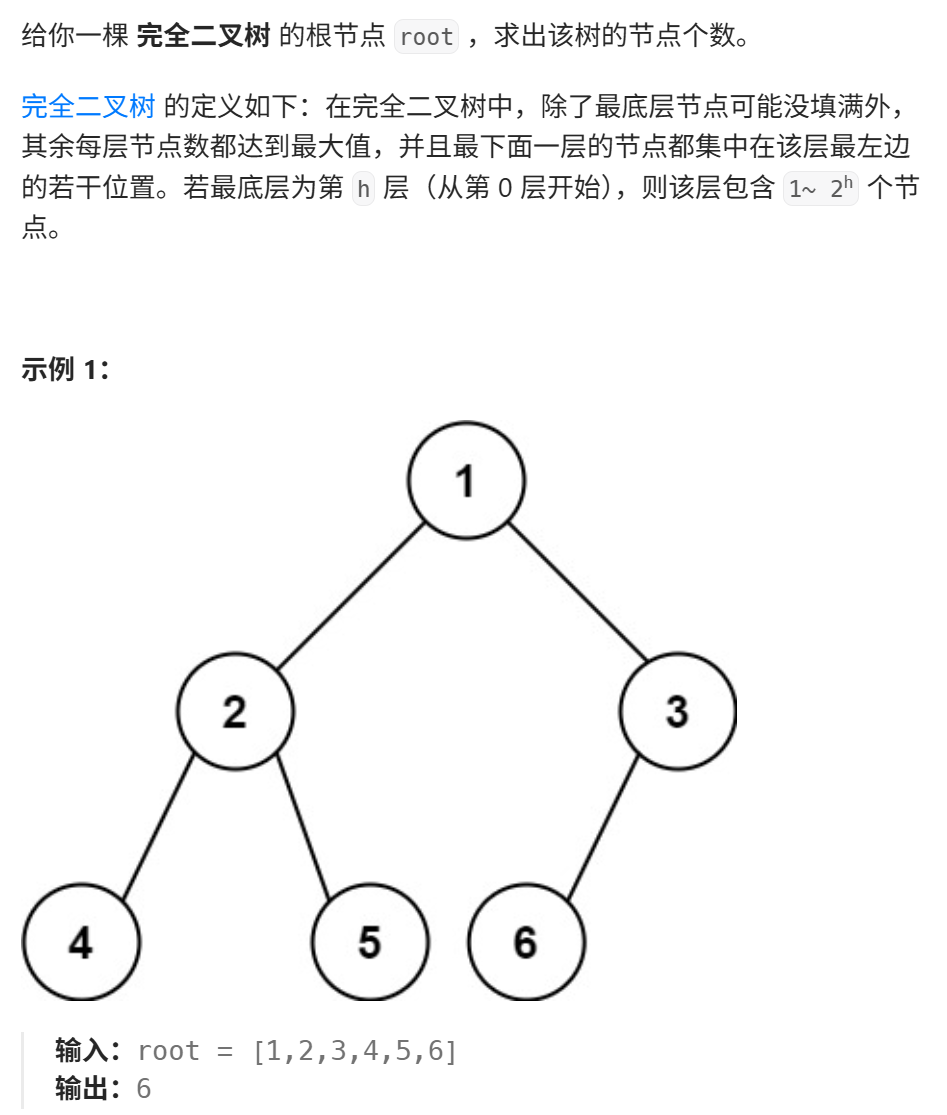
 　方法一：用普适的递归方法来做，这样会遍历到每一个节点。没有利用完全二叉树的性质。

class Solution {
    public int countNodes(TreeNode root) {
        if(root == null){
            return 0;
        }
        return countNodes(root.left) + countNodes(root.right) + 1;
    }
}
//时间复杂度：O（n）

　　方法二：充分利用了“完全二叉树”的结构，避免了重复计算完整子树的节点个数，大大减少了递归次数，因此时间复杂度从 O(n) 降低到了 O((log n)^2)，在大数据量时性能优势明显。

• 完全二叉树的特点是：左子树深度等于右子树深度 ⇒ 整个左子树是满二叉树，节点数是 2^depth - 1。

• 利用这一性质，可以直接跳过对整棵子树的递归计算，用位运算直接得出节点数。

class Solution {
    public int countNodes(TreeNode root) {
        if(root == null){
            return 0;
        }
        int left = countLevel(root.left);
        int right = countLevel(root.right);
        if(left == right){
            return countNodes(root.right) + (1<<left);
        }else{
            return countNodes(root.left) + (1<<right);
        }
    }

    public int countLevel(TreeNode root){
        int level = 0;
        while(root != null){
            level++;
            root = root.left;
        }
        return level;
    }
}
//时间复杂度：O（logn * logn）

二、平衡二叉树

 https://leetcode.cn/problems/balanced-binary-tree/description/?envType=problem-list-v2&envId=8At1GmaZ

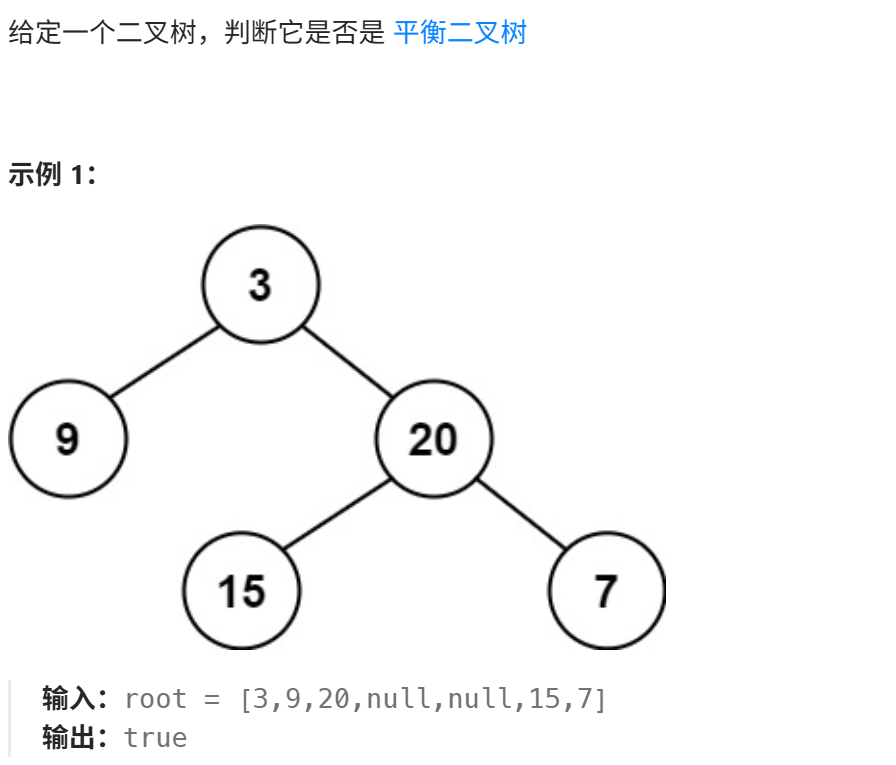
 　　方法：后序遍历+剪枝。每个节点只遍历一次，一旦某个子树不是平衡的，直接向上传递 -1，避免不必要的递归。

class Solution {
    public boolean isBalanced(TreeNode root) {
        return dfs(root)!=-1;
    }

    public int dfs(TreeNode root){
        //终止条件
        if(root == null){
            return 0;
        }
        int left = dfs(root.left);
        if(left == -1)  return -1;
        int right = dfs(root.right);
        if(right == -1) return -1;
        if(Math.abs(left-right) > 1)    return -1;
        return Math.max(left, right) + 1;
    }
}   
//时间复杂度：O（n）

三、二叉树的所有路径

 https://leetcode.cn/problems/binary-tree-paths/description/?envType=problem-list-v2&envId=8At1GmaZ

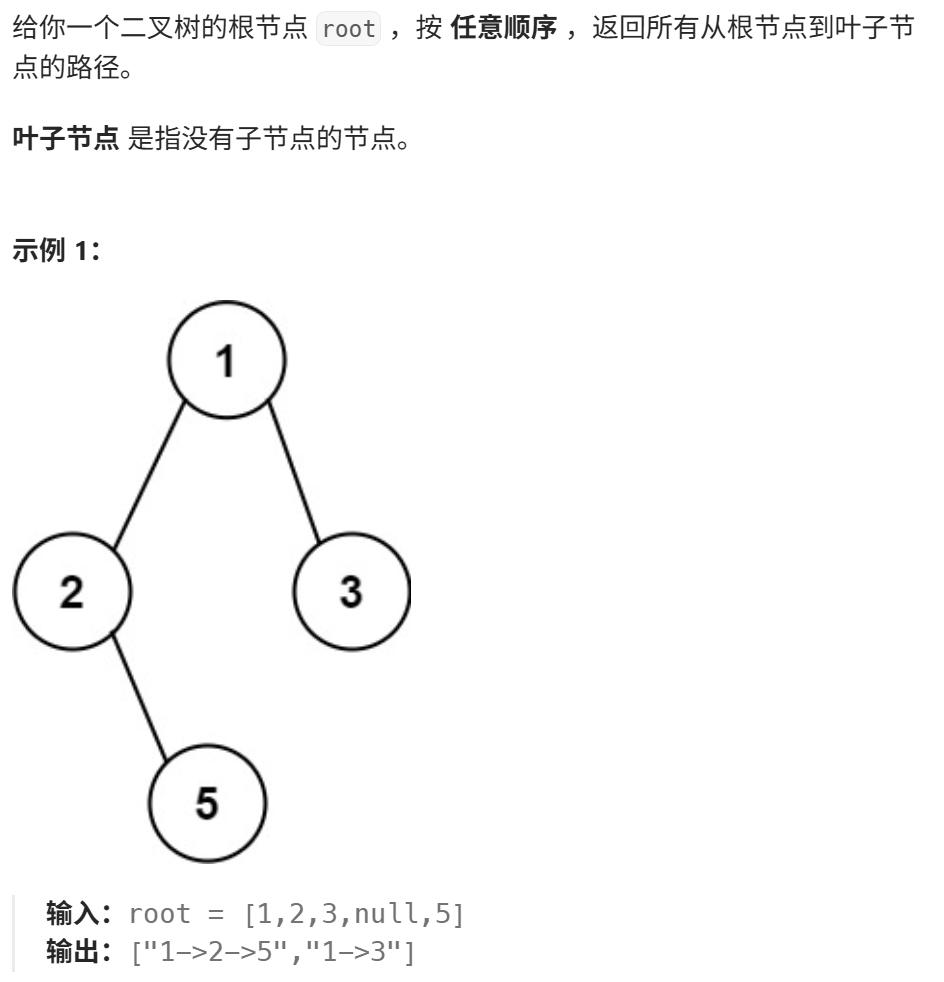
 　　主要思路：就是用dfs回溯，使用 DFS 遍历整棵树；每走一步把当前节点值加入路径；如果到达叶子节点，就将完整路径加入结果列表；否则继续递归左右子树。

class Solution {
    static List<String> res;
    public List<String> binaryTreePaths(TreeNode root) {
        res = new ArrayList<>();
        if(root == null){
            return res;
        }
        StringBuilder sb = new StringBuilder();
        dfs(root, sb);
        return res;
    }


    public void dfs(TreeNode root,StringBuilder sb){
        int len = sb.length();
        //走到叶子节点
        sb.append(root.val);




        if(root.left == null && root.right == null){
            res.add(sb.toString());
        }else{  
            sb.append("->");
            if(root.left!=null) dfs(root.left, sb);
            if(root.right!=null) dfs(root.right, sb);
        }
        sb.setLength(len);
    }
}

      1
     / \
    2   3
     \
      5
第一步：从根节点 1 开始
当前路径："1->"

接着递归左子树 2

第二步：递归到 2
当前路径："1->2->"

再递归右子树 5（因为 2 没有左子树）

第三步：递归到 5
当前路径："1->2->5"

5 是叶子节点 ⇒ 将该路径加入结果集

🔁 递归返回到 2 ⇒ 返回到 1 ⇒ 再递归右子树 3

第四步：递归到 3
当前路径："1->3"

3 是叶子节点 ⇒ 将该路径加入结果集

四、左叶子之和

 　　https://leetcode.cn/problems/sum-of-left-leaves/description/?envType=problem-list-v2&envId=8At1GmaZ

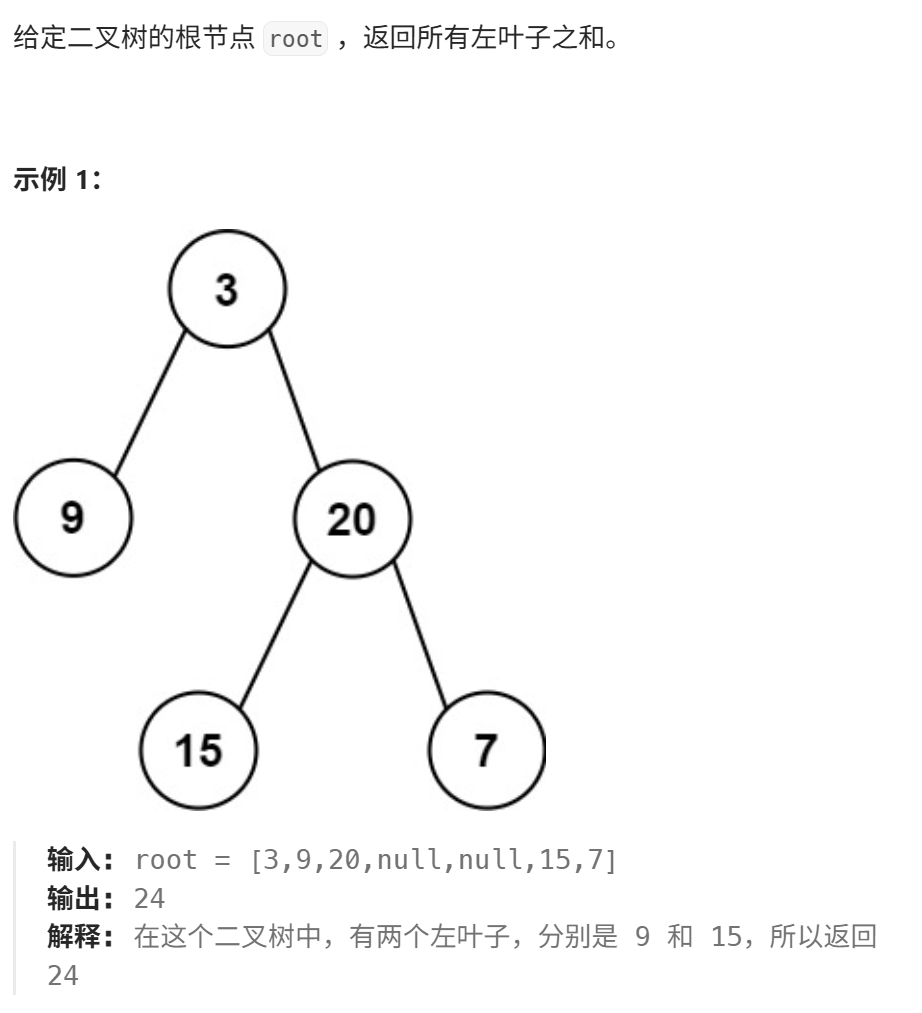
 　　方法一：DFS回溯法，递归计算左右子树的左叶子节点的值。

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        return dfs(root);
    }

    public int dfs(TreeNode root){
        if(root == null){
            return 0;
        }
        if(root.left == null && root.right == null){
            return 0;
        }
        int leftNum = dfs(root.left);
        if(root.left != null && root.left.left == null && root.left.right == null){
            leftNum = root.left.val;
        }
        int rightNum = dfs(root.right);
        int sum = leftNum + rightNum;
        return sum;
    }
}

　　方法二：层序遍历

class Solution{
    public int sumOfLeftLeaves(TreeNode root) {
        if(root == null){
            return 0;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int sum = 0;
        while(!queue.isEmpty()){
            int size = queue.size();
            for(int i=0; i<size; i++){
                TreeNode cur = queue.poll();
                if(cur.left != null && cur.left.left == null && cur.left.right == null){
                    sum += cur.left.val;
                }
                if(cur.left != null)    queue.offer(cur.left);
                if(cur.right != null)   queue.offer(cur.right);
            }
        }
        return sum;
    }
}